Задачи на готовых чертежах по теме "Многоугольники"

Задачи на готовых чертежах Многоугольники

Многоугольники

параллелограмм

прямоугольник

ромб

Правильные

многоугольники

трапеция

Задачи на готовых чертежах Параллелограмм

1

2

3

4

5

6

7

8

?

№ 1

Е

В

С

o

32

D

А

ABCD – параллелограмм.

Найти : С, D.

?

10 см

№ 2

K

N

0

60

2 см

E

M

P

MNKP – параллелограмм.

Найти: MP , PK .

?

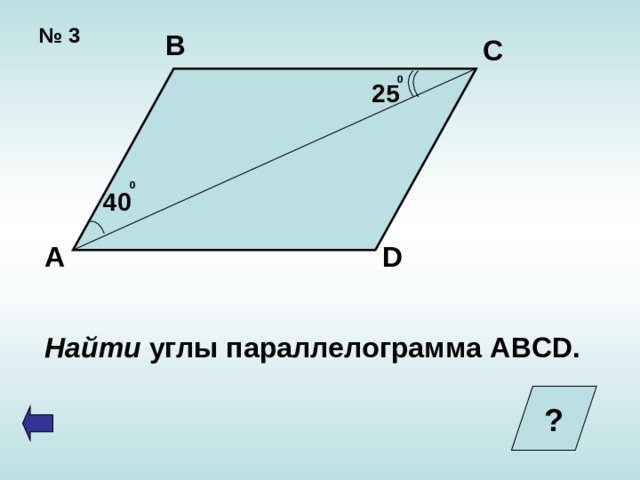
№ 3

В

С

0

25

0

40

А

D

Найти углы параллелограмма ABCD.

?

А

№ 4

В

D

2

E

C

3

ABCD – параллелограмм.

Найти: Р

?

ABCD

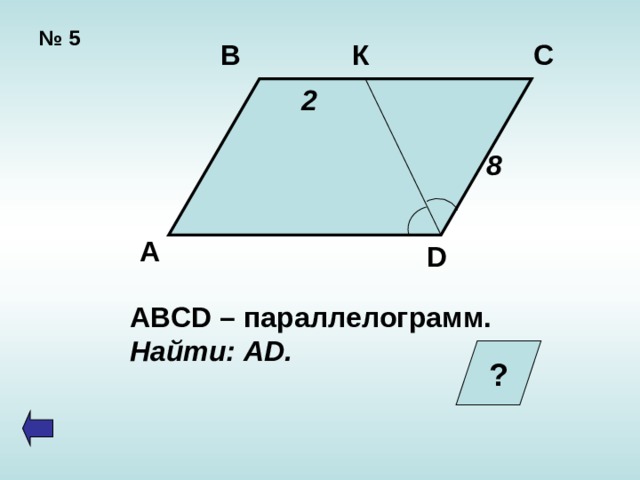
№ 5

В

К

С

2

8

А

D

ABCD – параллелограмм.

Найти: AD.

?

В

С

К

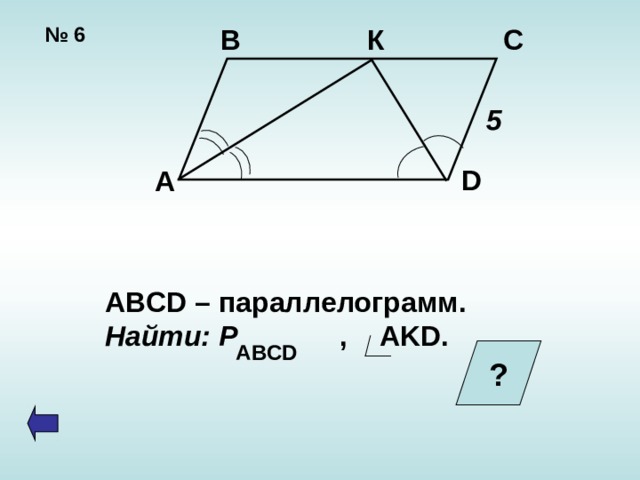
№ 6

5

D

А

ABCD – параллелограмм.

Найти: Р , AKD.

ABCD

?

5 см

№ 7

B

C

F

D

N

A

4 см

NBFD – параллелограмм.

Найти: ВС, CD.

?

7 см

№ 8

C

B

N

M

K

D

A

P

ABCD – параллелограмм , P = 20 c м.

Найти: MN, MP.

MNKP

?

////

////

Параллелограмм

Определение Свойства Признаки

С

В

ABCD –

параллелограмм,

если:

• AB=CD, AB||CD

или BC=AD,

BC||AD.

2. AB=CD, BC=AD.

3. AC BD=O,

AO = CO , BO = DO

\\\

• AO = CO , BO = DO,

O=AC BD

2. AB=CD, BC=AD

3. A= C, B= D

-

=

О

-

=

\\\

D

А

AB || DC

AD || BC

Задачи на готовых чертежах

Трапеция

1

2

3

4

8

5

6

7

?

=

№ 1

В

С

=

=

А

D

ABCD – трапеция.

Найти: углы трапеции.

?

№ 2

В

С

0

75

0

40

А

D

K

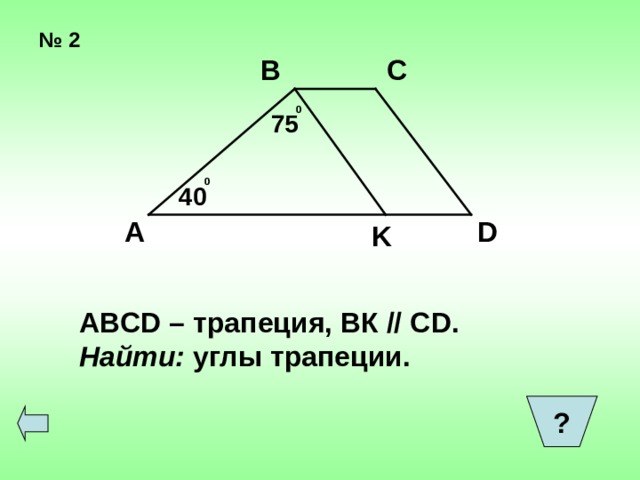
ABCD – трапеция, ВК // С D.

Найти: углы трапеции.

?

№ 3

В

С

o

135

o

45

D

А

30 см

ABCD – трапеция.

Найти: ВС.

?

№ 4

5 см

В

С

=

=

D

А

K

ABCD – трапеция , AD = 15 c м .

Найти: СК.

?

=

=

№ 5

5 см

В

С

о

30

О

о

60

D

К

А

ABCD – трапеция , AD = 15 c м .

Найти: P .

ABCD

?

№ 6

С

В

5 см

=

=

о

о

60

60

М

А

К

Р

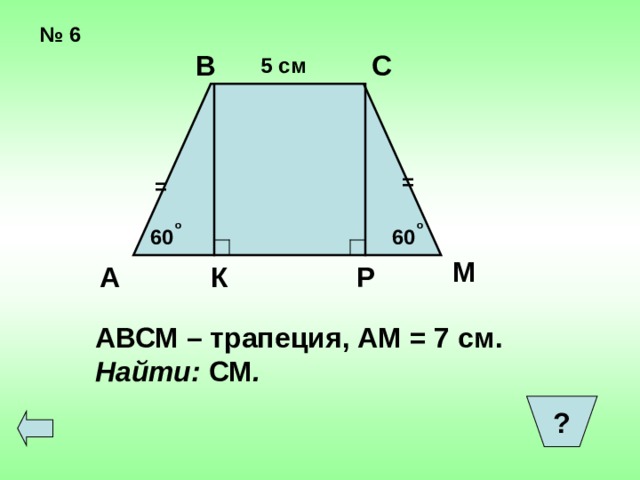
АВСМ – трапеция, АМ = 7 см.

Найти: СМ .

?

=

№ 7

В

С

=

о

50

D

А

АВС D – трапеция.

Найти: В

?

№ 8

В

С

a

D

А

b

K

АВС D – трапеция .

Найти: АК и А D.

?

Трапеция

Равнобокая трапеция:

АС = В D,

A = D, B = C

Прямоугольная трапеция:

Верхнее

основание

В

С

В

С

О

N

M

=

=

O

Средняя линия

D

А

D

Нижнее основание

А

ВС // А D

MN = 0,5(BC + AD)

C

B

D

A

Задачи на готовых чертежах.

Прямоугольник.

4

1

2

5

6

3

?

№ 1

В

С

о

40

O

K

D

А

ABCD – прямоугольник.

Найти: АВК .

?

=

=

=

=

D

№ 2

E

C

30

о

_

_

F

B

_

_

A

K

M

АСЕК – прямоугольник, ВС = 5 см.

Найти: Р .

BDFM

?

№ 3

В

С

А

D

M

N

ABCD – прямоугольник.

Доказать: AM = ND.

?

№ 4

В

С

60

о

О

D

А

ABCD – прямоугольник.

Найти: АОВ, ВОС

?

№ 5

В

С

о

60

О

К

D

А

ABCD – прямоугольник, ОК = 2 см.

Найти: АС, АВ.

?

4 см

6 см

В

№ 6

К

С

о

75

D

А

ABCD – прямоугольник.

Найти: AD .

?

Прямоугольник

Определение Свойства Признаки

С

В

ABCD –

прямоугольник,

если:

1. ABCD –

параллелограмм

и АС = В D .

2. ABCD –

параллелограмм

и А = 90 .

3. А = В = С =90 .

• АС = В D.

2. Прямоугольник

обладает всеми

свойствами

параллелограмма.

О

D

А

ABCD –

параллелограмм ,

А = В = С = D =

= 90 .

свойства

о

о

Задачи на готовых чертежах.

Ромб.

1

2

3

4

5

?

6 см

№ 1

В

С

N

о

60

А

M

D

ABCD – ромб.

Найти: MD + DN.

?

С

№ 2

В

Е

о

75

А

К

D

ABCD – ромб.

Найти: СВЕ.

?

№ 3

В

С

о

55

D

А

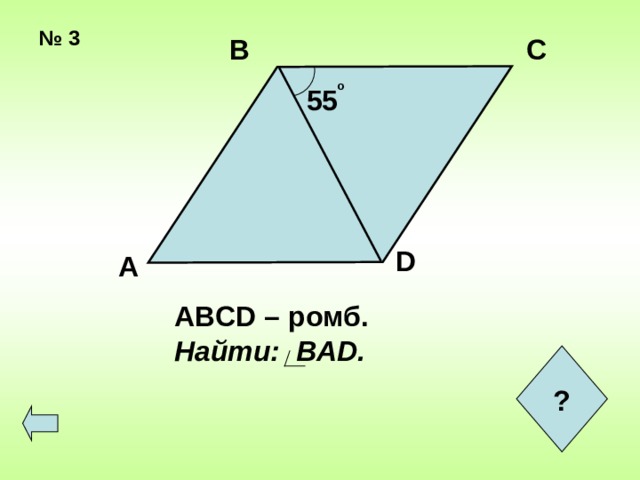
ABCD – ромб.

Найти: BAD.

?

№ 4

В

о

35

А

С

ABCD – ромб.

Найти: AB С.

?

D

В

№ 5

ABCD – ромб.

Найти: C.

С

А

о

150

Е

?

D

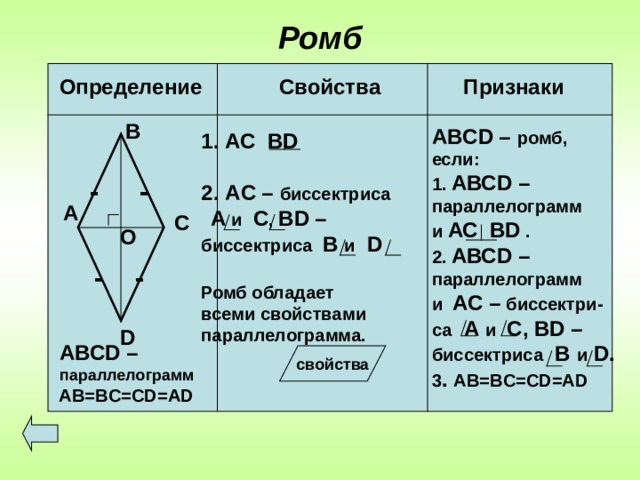
Ромб

Определение Свойства Признаки

В

ABCD – ромб,

если:

1. АВС D –

параллелограмм

и АС В D .

2. АВС D –

параллелограмм

и AC – биссектри-

са А и С, BD –

биссектриса В и D .

3 . AB=BC=CD=AD

• АС В D

2. AC – биссектриса

А и С , BD –

биссектриса В и D

Ромб обладает

всеми свойствами

параллелограмма.

-

-

А

С

О

-

-

D

АВС D –

параллелограмм

свойства

AB=BC=CD=AD

Задачи на готовых чертежах

Правильные многоугольники

2

1

3

7

4

5

6

?

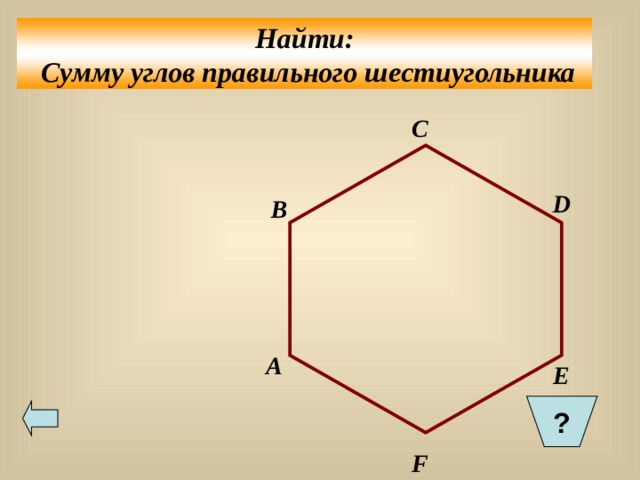
Найти:

Сумму углов правильного шестиугольника

С

D

B

A

E

?

F

Дано:

ABCDEF – правильный шестиугольник

С

Найти:

Величину угла В

D

B

A

E

?

F

Дано:

ABCDEF – правильный шестиугольник

АВ = 7 см

С

D

B

Найти:

Периметр ABCDEF

A

E

?

F

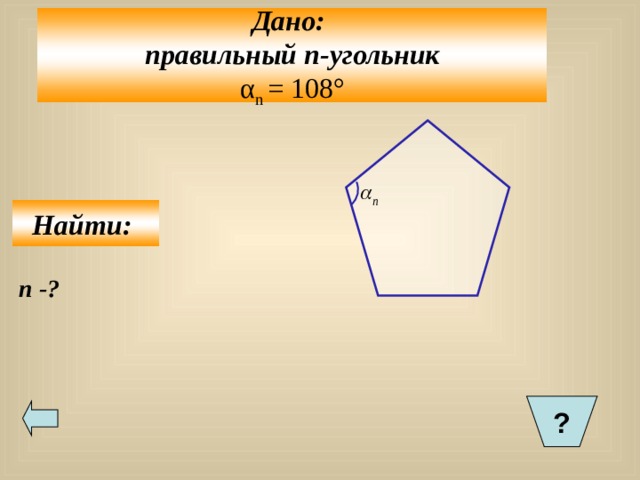
Дано:

правильный n- угольник

α n = 108°

Найти:

n -?

?

Дано: n = 1 2

Найти: α n = ? и S n = ?

?

Чему равен каждый из углов правильного многоугольника:

1 группа

• пятиугольника;
• n – угольника.

2 группа

• восьмиугольника;
• n – угольника.

3 группа

• десятиугольника;
• n – угольника.

4 группа

• восемнадцатиугольника;
• n – угольника.

?

?

В таблице заполните пустые клетки (  n -угол правильного n- угольника, n- сторон, S n - сумма углов правильного n -угольника). Решение задач записать в тетрадь.

№

1)

n

?

2)

S n

 n

?

20

3)

108 °

?

?

?

1260 °

?

?

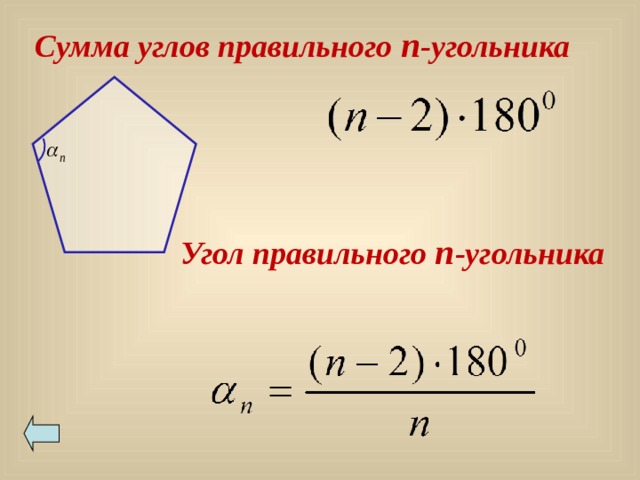
Сумма углов правильного n -угольника

Угол правильного n - угольника

Литература

• Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7-9 класс.- М.: Просвещение, 2015.