ЗАДАНИЕ 23 ОГЭ.
ФУНКЦИИ И ИХ СВОЙСТВА. ГРАФИКИ ФУНКЦИЙ.
ПАРАБОЛЫ
(49) Постройте график функции 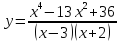 и определите, при каких значениях параметра
и определите, при каких значениях параметра 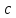 прямая
прямая 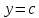 имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
Решение.
Найдём область определения данной функции. Т.к. знаменатель не может равняться нулю, то 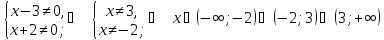 . Значит,
. Значит,
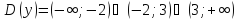 .
.
Упростим выражение, задающее функцию. Для этого разложим на множители числитель. Воспользуемся методом разложения на множители с помощью квадратного уравнения.
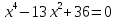
Выполним замену переменной: 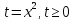
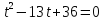
Используя теорему Виета, находим корни:
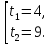
Тогда, 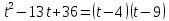 ,
,
Значит, 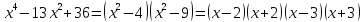 .
.
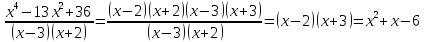 .
.
Итак, исходная функция, после упрощения, имеет вид:
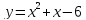 . Это квадратичная функция, графиком её является парабола с вершиной в точке
. Это квадратичная функция, графиком её является парабола с вершиной в точке 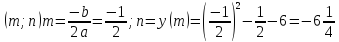 ; ветви направлены вверх, т.к.
; ветви направлены вверх, т.к. 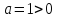 . График этой функции получается из графика функции
. График этой функции получается из графика функции 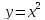 смещением вдоль оси Ох на
смещением вдоль оси Ох на 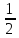 ед. отрезка вправо, и вдоль оси Оу на
ед. отрезка вправо, и вдоль оси Оу на 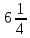 ед. отрезка вниз.
ед. отрезка вниз.
Так как область определения функции не содержит значения 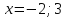 , то, для того, чтобы выколоть точки на графике, которые не удовлетворяют области определения, найдём ординаты этих точек:
, то, для того, чтобы выколоть точки на графике, которые не удовлетворяют области определения, найдём ординаты этих точек:
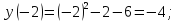
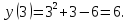
Значит, на графике выкалываем точки 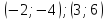 .
.
Прямая 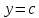 проходит через точку
проходит через точку 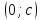 параллельно оси Ох, она будет пересекать параболу только в одной точке, если она проходит либо через вершину параболы, т.е.
параллельно оси Ох, она будет пересекать параболу только в одной точке, если она проходит либо через вершину параболы, т.е. 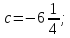 либо через выколотые точки, т.е.
либо через выколотые точки, т.е.  .
.
Ответ:  .
.
(338207) Постройте график функции  и определите, при каких значениях параметра
и определите, при каких значениях параметра  прямая
прямая  имеет с графиком ровно две общие точки.
имеет с графиком ровно две общие точки.
Решение.
Найдём область определения данной функции. Т.к. знаменатель не может равняться нулю, то . Значит,
.
Упростим выражение, задающее функцию. Для этого разложим на множители числитель и знаменатель методом вынесения за скобки общего множителя.
Итак, исходная функция, после упрощения, имеет вид:
 . Это квадратичная функция, графиком её является парабола с вершиной в точке
. Это квадратичная функция, графиком её является парабола с вершиной в точке  ; ветви направлены вниз, т.к.
; ветви направлены вниз, т.к.  . График этой функции получается из графика функции
. График этой функции получается из графика функции  смещением вдоль оси Оу на
смещением вдоль оси Оу на  ед. отрезка вниз.
ед. отрезка вниз.
Так как область определения функции не содержит значения  , то, для того, чтобы выколоть точки на графике, которые не удовлетворяют области определения, найдём ординаты этих точек:
, то, для того, чтобы выколоть точки на графике, которые не удовлетворяют области определения, найдём ординаты этих точек:


Значит, на графике выкалываем точки  .
.
Прямая  проходит через точку
проходит через точку  параллельно оси Ох, она будет пересекать параболу ровно в двух точках, если она не проходит через точки
параллельно оси Ох, она будет пересекать параболу ровно в двух точках, если она не проходит через точки  , причём,
, причём,  , т.е.
, т.е.  .
.
Ответ: 
(338408) Постройте график функции и определите, при каких значениях  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
Решение.
Найдём область определения данной функции. Т.к. знаменатель не может равняться нулю, то . Значит,
.
Упростим выражение, задающее функцию.
Итак, исходная функция, после упрощения, имеет вид:  . Это квадратичная функция, графиком её является парабола с вершиной в точке
. Это квадратичная функция, графиком её является парабола с вершиной в точке  ; ветви направлены вниз, т.к.
; ветви направлены вниз, т.к.  . График этой функции получается из графика функции
. График этой функции получается из графика функции  смещением вдоль оси Оу на
смещением вдоль оси Оу на  ед. отрезка вниз.
ед. отрезка вниз.
Так как область определения функции не содержит значение  , то, для того, чтобы выколоть точку на графике, которая не удовлетворяют области определения, найдём ординату этой точки:
, то, для того, чтобы выколоть точку на графике, которая не удовлетворяют области определения, найдём ординату этой точки:

Значит, на графике выкалываем точку  .
.
 является прямой пропорциональностью, её графиком прямая, проходящая через точку
является прямой пропорциональностью, её графиком прямая, проходящая через точку  . Она будет пересекать параболу ровно в одной точке, если:
. Она будет пересекать параболу ровно в одной точке, если:
1) уравнение  будет иметь только одно решение, т.е. если дискриминант будет равен нулю;
будет иметь только одно решение, т.е. если дискриминант будет равен нулю;
2) уравнение  имеет два решения, одно из которых равно 1 (абсцисса выколотой точки), т.е. дискриминант положителен, и
имеет два решения, одно из которых равно 1 (абсцисса выколотой точки), т.е. дискриминант положителен, и  .
.
Рассмотрим каждый из этих случаев.
1) 

Т.к.  , то
, то 

Значит, прямая пересекает параболу в одной точке, если она задана формулой  или
или  .
.
2) Т.к.  , то
, то 

По теореме Виета
Значит, прямая, пересекающая параболу в одной точке задана формулой  .
.
Итак, прямая  имеет с графиком функции ровно одну общую точку при
имеет с графиком функции ровно одну общую точку при 
Ответ:
(341342) Постройте график функции и определите, при каких значениях  прямая
прямая  не имеет с графиком ни одной общей точки.
не имеет с графиком ни одной общей точки.
Решение.
Найдём область определения данной функции. Т.к. знаменатель не может равняться нулю, то . Значит,
.
Упростим выражение, задающее функцию.
Тогда
1). Если  , то
, то  – квадратная функция, графиком является парабола с вершиной в точке
– квадратная функция, графиком является парабола с вершиной в точке  , ветви направлены вверх, т.к.
, ветви направлены вверх, т.к.  . График этой функции получается из графика функции
. График этой функции получается из графика функции 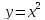 сжатием к оси Ох в 2 раза.
сжатием к оси Ох в 2 раза.
Так как  , то
, то  , т.е. выколотая точка имеет координаты
, т.е. выколотая точка имеет координаты  .
.
2). Если  , то
, то  - квадратная функция, графиком является парабола с вершиной в точке
- квадратная функция, графиком является парабола с вершиной в точке  , ветви направлены вниз, т.к.
, ветви направлены вниз, т.к.  . График этой функции получается из графика функции
. График этой функции получается из графика функции  сжатием к оси Ох в 2 раза.
сжатием к оси Ох в 2 раза.
Поскольку график располагается в двух полуплоскостях от оси Ох, то единственный случай, когда прямая  не имеет с этим графиком ни одной общей точки, это тот случай, когда прямая, параллельная оси Ох проходит через выколотую точку, т. е. через точку
не имеет с этим графиком ни одной общей точки, это тот случай, когда прямая, параллельная оси Ох проходит через выколотую точку, т. е. через точку  . В это случае
. В это случае  и
и  .
.
Ответ: 8
(341394) Постройте график функции и определите, при каких значениях  прямая
прямая  имеет с графиком одну или две общие точки.
имеет с графиком одну или две общие точки.
Решение.
Если  , то . Это квадратичная функция, графиком является парабола, с вершиной в точке
, то . Это квадратичная функция, графиком является парабола, с вершиной в точке  , ветви направлены вверх, т.к.
, ветви направлены вверх, т.к. 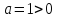 . График этой функции получается из графика функции
. График этой функции получается из графика функции 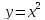 смещением вдоль оси Ох на 4 ед. отрезка влево.
смещением вдоль оси Ох на 4 ед. отрезка влево.
Если  , то
, то  . Это обратная пропорциональность, графиком является гипербола, расположенная во II и IV четверти, т.к.
. Это обратная пропорциональность, графиком является гипербола, расположенная во II и IV четверти, т.к.  . Но т.к.
. Но т.к.  , то в нашем, конкретном, случае гипербола будет располагаться только во II четверти и проходить через точки .
, то в нашем, конкретном, случае гипербола будет располагаться только во II четверти и проходить через точки .
По графику определяем, что прямая  будет иметь с графиком данной функции одну или две общие точки, если
будет иметь с графиком данной функции одну или две общие точки, если  , а также, если
, а также, если  (т.к. гипербола не пересекает ось Ох).
(т.к. гипербола не пересекает ось Ох).
Ответ:  .
.
(340852, 338714, 353418) Найдите все значения  , при каждом из которых прямая
, при каждом из которых прямая  имеет с графиком функции
имеет с графиком функции  ровно одну общую точку. Постройте этот график и все такие прямые.
ровно одну общую точку. Постройте этот график и все такие прямые.
Решение.
Для того, чтобы найти общую точку графиков двух функций, нужно решить уравнение  . Это квадратное уравнение, значит, условие единственности общей точки достигается в случае, когда дискриминант равен нулю.
. Это квадратное уравнение, значит, условие единственности общей точки достигается в случае, когда дискриминант равен нулю.


Так как  то
то 
Значит, прямые задаются формулами  и
и  .
.
 - квадратичная функция, графиком является парабола, с вершиной в точке
- квадратичная функция, графиком является парабола, с вершиной в точке  , ветви направлены вверх, т.к.
, ветви направлены вверх, т.к. 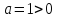 . График этой функции получается из графика функции
. График этой функции получается из графика функции 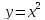 смещением вдоль оси Оу на 4 ед. отрезка вверх.
смещением вдоль оси Оу на 4 ед. отрезка вверх.
 – прямая пропорциональность, графиком является прямая, проходящая через точки
– прямая пропорциональность, графиком является прямая, проходящая через точки  .
.
 – прямая пропорциональность, графиком является прямая, проходящая через точки
– прямая пропорциональность, графиком является прямая, проходящая через точки  .
.
Ответ:  .
.
(127, 314793) При каком значении  прямая
прямая  имеет с параболой
имеет с параболой  ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении
ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении  .
.
Решение.
Для того, чтобы найти общую точку графиков двух функций, нужно решить уравнение  . Это квадратное уравнение, значит, условие единственности общей точки достигается в случае, когда дискриминант равен нулю.
. Это квадратное уравнение, значит, условие единственности общей точки достигается в случае, когда дискриминант равен нулю.

Так как  то
то  . Тогда
. Тогда




Значит, прямая  имеет с параболой
имеет с параболой  одну общую точку
одну общую точку  при
при  .
.
 – квадратичная функция, графиком является парабола с вершиной в точке
– квадратичная функция, графиком является парабола с вершиной в точке  где
где 

т.е. в точке  , ветви параболы направлены вверх, т.к.
, ветви параболы направлены вверх, т.к. 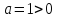 . График этой функции получается из графика функции
. График этой функции получается из графика функции 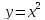 смещением вдоль оси Ох на 1 ед. отрезок влево, и вдоль оси Оу на 1 ед. отрезок вниз.
смещением вдоль оси Ох на 1 ед. отрезок влево, и вдоль оси Оу на 1 ед. отрезок вниз.
 – линейная функция, графиком является прямая, проходящая через точки
– линейная функция, графиком является прямая, проходящая через точки  .
.
Ответ: 
(179, 314798) При каких отрицательных значениях  прямая
прямая  имеет с параболой
имеет с параболой  ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
Решение.
Для того, чтобы найти общую точку графиков двух функций, нужно решить уравнение  . Это квадратное уравнение, значит, условие единственности общей точки достигается в случае, когда дискриминант равен нулю.
. Это квадратное уравнение, значит, условие единственности общей точки достигается в случае, когда дискриминант равен нулю.

Так как  , то
, то 

По условию  должно принимать отрицательные значения, значит,
должно принимать отрицательные значения, значит,  – посторонний корень.
– посторонний корень.
Тогда квадратное уравнение принимает вид:  . Найдём ординату точки пересечения:
. Найдём ординату точки пересечения:  . Графики имеют общую точку
. Графики имеют общую точку  .
.
 – квадратичная функция, графиком является парабола с вершиной в точке
– квадратичная функция, графиком является парабола с вершиной в точке  где
где 

т.е. в точке  , ветви параболы направлены вверх, т.к.
, ветви параболы направлены вверх, т.к. 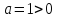 . График этой функции получается из графика функции
. График этой функции получается из графика функции 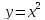 смещением вдоль оси Ох на 1 ед. отрезок влево, и вдоль оси Оу на 1 ед. отрезок вниз.
смещением вдоль оси Ох на 1 ед. отрезок влево, и вдоль оси Оу на 1 ед. отрезок вниз.
 – линейная функция, графиком является прямая, проходящая через точки
– линейная функция, графиком является прямая, проходящая через точки  .
.
Ответ:  .
.
(311576) Известно, что парабола проходит через точку  и её вершина находится в начале координат. Найдите уравнение этой параболы и вычислите, в каких точках она пересекает прямую
и её вершина находится в начале координат. Найдите уравнение этой параболы и вычислите, в каких точках она пересекает прямую  .
.
Решение.
По условию известно, что вершина параболы находится в начале координат, значит, квадратичная функция задана формулой  . Т.к. эта парабола проходит через точку
. Т.к. эта парабола проходит через точку  , то
, то  . Формула принимает вид:
. Формула принимает вид:  .
.
Поскольку прямая  и парабола
и парабола  пересекаются, то:
пересекаются, то:
 . Значит, графики данных функций пересекаются в точках
. Значит, графики данных функций пересекаются в точках  .
.
Ответ: .
(314398) Парабола проходит через точки . Найдите координаты её вершины.
Решение.
Так как парабола проходит через точки , то координаты этих точек удовлетворяют уравнению параболы  . Значит,
. Значит,
Тогда квадратичная функция задана уравнением:  . Найдём координаты вершины этой параболы.
. Найдём координаты вершины этой параболы.
 – вершина параболы.
– вершина параболы.
Ответ: 
(314407) При каких значениях  вершины парабол
вершины парабол  и
и  расположены по разные стороны от оси
расположены по разные стороны от оси  ?
?
Решение.
Вершины двух парабол расположены по разные стороны от оси Ох, если их ординаты имеют разные знаки. Найдём эти ординаты по формуле  .
.
Т.к.  и
и  должны иметь разные знаки, то их произведение должно быть отрицательным.
должны иметь разные знаки, то их произведение должно быть отрицательным.

Ответ:
(314458) При каких значениях  вершины парабол
вершины парабол  и
и  расположены по одну сторону от оси
расположены по одну сторону от оси  ?
?
Решение.
Вершины двух парабол расположены по одну сторону от оси Ох, если их ординаты имеют одинаковые знаки. Найдём эти ординаты по формуле  .
.
Т.к.  и
и  должны иметь одинаковые знаки, то их произведение должно быть положительным.
должны иметь одинаковые знаки, то их произведение должно быть положительным.
Так как  при любом значении
при любом значении  , то разделив обе части неравенства на этот множитель, получим:
, то разделив обе части неравенства на этот множитель, получим:

Ответ: .
.
(314685) Известно, что графики функций  и
и  имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
Решение.
Для того, чтобы найти общую точку графиков двух функций, нужно решить уравнение  . Это квадратное уравнение, значит, условие единственности общей точки достигается в случае, когда дискриминант равен нулю.
. Это квадратное уравнение, значит, условие единственности общей точки достигается в случае, когда дискриминант равен нулю.

Так как  , то
, то  и квадратное уравнение принимает вид:
и квадратное уравнение принимает вид:


Найдём ординату точки пересечения.

Итак, графики имеют одну общую точку  при
при  .
.
 – квадратичная функция, графиком является парабола с вершиной в точке
– квадратичная функция, графиком является парабола с вершиной в точке  , ветви направлены вверх, т.к.
, ветви направлены вверх, т.к. 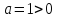 . График этой функции получается из графика функции
. График этой функции получается из графика функции 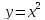 смещением вдоль оси Оу на 1 ед. отрезок вниз.
смещением вдоль оси Оу на 1 ед. отрезок вниз.
 – линейная функция, графиком является прямая, проходящая через точки
– линейная функция, графиком является прямая, проходящая через точки  .
.
Ответ:  .
.
(339055) Найдите  и постройте в одной системе координат прямую
и постройте в одной системе координат прямую  и график функции
и график функции  , если известно, что этот график имеет с прямой ровно одну общую точку.
, если известно, что этот график имеет с прямой ровно одну общую точку.
Решение.
Для того, чтобы найти общую точку графиков двух функций, нужно решить уравнение  . Это квадратное уравнение, значит, условие единственности общей точки достигается в случае, когда дискриминант равен нулю.
. Это квадратное уравнение, значит, условие единственности общей точки достигается в случае, когда дискриминант равен нулю.


Так как  , то
, то  и квадратное уравнение принимает вид:
и квадратное уравнение принимает вид:


Найдём ординату точки пересечения.

Итак, графики имеют одну общую точку  при
при  .
.
 – квадратичная функция, графиком является парабола с вершиной в точке
– квадратичная функция, графиком является парабола с вершиной в точке  , ветви направлены вверх, т.к.
, ветви направлены вверх, т.к. 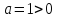 . График этой функции получается из графика функции
. График этой функции получается из графика функции 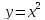 смещением вдоль оси Оу на 1 ед. отрезок вверх.
смещением вдоль оси Оу на 1 ед. отрезок вверх.
 – прямая пропорциональность, графиком является прямая, проходящая через точки
– прямая пропорциональность, графиком является прямая, проходящая через точки 
Ответ: 
ЗАДАЧИ
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
(388288) Постройте график функции и определите, при каких значениях параметра  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
(341129) Постройте график функции и определите, при каких значениях параметра  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
(341159) Постройте график функции и определите, при каких значениях параметра  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
(338295) Постройте график функции и определите, при каких значениях параметра  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
(353520) Постройте график функции и определите, при каких значениях параметра  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
(341535) Постройте график функции  и определите, при каких значениях параметра
и определите, при каких значениях параметра  прямая
прямая  имеет с графиком ровно две общие точки.
имеет с графиком ровно две общие точки.
(341686, 350611) Постройте график функции и определите, при каких значениях  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
(348483) Постройте график функции и определите, при каких значениях  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
(348845) Постройте график функции и определите, при каких значениях  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
(353416) Постройте график функции и определите, при каких значениях  прямая
прямая  не имеет с графиком ни одной общей точки.
не имеет с графиком ни одной общей точки.
(341368) Постройте график функции  и определите, при каких значениях
и определите, при каких значениях  прямая
прямая  имеет с графиком три общие точки.
имеет с графиком три общие точки.
(338909) Найдите все значения  , при каждом из которых прямая
, при каждом из которых прямая  имеет с графиком функции
имеет с графиком функции  ровно одну общую точку. Постройте этот график и все такие прямые.
ровно одну общую точку. Постройте этот график и все такие прямые.
(348835) Найдите все значения  , при каждом из которых прямая
, при каждом из которых прямая  имеет с графиком функции
имеет с графиком функции  ровно одну общую точку. Постройте этот график и все такие прямые.
ровно одну общую точку. Постройте этот график и все такие прямые.
(348859) Найдите все значения  , при каждом из которых прямая
, при каждом из которых прямая  имеет с графиком функции
имеет с графиком функции  ровно одну общую точку. Постройте этот график и все такие прямые.
ровно одну общую точку. Постройте этот график и все такие прямые.
(349123) Найдите все значения  , при каждом из которых прямая
, при каждом из которых прямая  имеет с графиком функции
имеет с графиком функции  ровно одну общую точку. Постройте этот график и все такие прямые.
ровно одну общую точку. Постройте этот график и все такие прямые.
(349838) Найдите все значения  , при каждом из которых прямая
, при каждом из которых прямая  имеет с графиком функции
имеет с графиком функции  ровно одну общую точку. Постройте этот график и все такие прямые.
ровно одну общую точку. Постройте этот график и все такие прямые.
(350560) Найдите все значения  , при каждом из которых прямая
, при каждом из которых прямая  имеет с графиком функции
имеет с графиком функции  ровно одну общую точку. Постройте этот график и все такие прямые.
ровно одну общую точку. Постройте этот график и все такие прямые.
(351246) Найдите все значения  , при каждом из которых прямая
, при каждом из которых прямая  имеет с графиком функции
имеет с графиком функции  ровно одну общую точку. Постройте этот график и все такие прямые.
ровно одну общую точку. Постройте этот график и все такие прямые.
(352224) Найдите все значения  , при каждом из которых прямая
, при каждом из которых прямая  имеет с графиком функции
имеет с графиком функции  ровно одну общую точку. Постройте этот график и все такие прямые.
ровно одну общую точку. Постройте этот график и все такие прямые.
(352325) Найдите все значения  , при каждом из которых прямая
, при каждом из которых прямая  имеет с графиком функции
имеет с графиком функции  ровно одну общую точку. Постройте этот график и все такие прямые.
ровно одну общую точку. Постройте этот график и все такие прямые.
(353304) Найдите все значения  , при каждом из которых прямая
, при каждом из которых прямая  имеет с графиком функции
имеет с графиком функции  ровно одну общую точку. Постройте этот график и все такие прямые.
ровно одну общую точку. Постройте этот график и все такие прямые.
(314791) При каком значении  прямая
прямая  имеет с параболой
имеет с параболой  ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении
ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении  .
.
(314792) При каком значении  прямая
прямая  имеет с параболой
имеет с параболой  ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении
ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении  .
.
(314794) При каком значении  прямая
прямая  имеет с параболой
имеет с параболой  ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении
ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении  .
.
(314790) При каких отрицательных значениях  прямая
прямая  имеет с параболой
имеет с параболой  ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
(314801) При каких положительных значениях  прямая
прямая  имеет с параболой
имеет с параболой  ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
(314797) При каких положительных значениях  прямая
прямая  имеет с параболой
имеет с параболой  ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
(314409) Парабола проходит через точки . Найдите координаты её вершины.
(314412) Парабола проходит через точки . Найдите координаты её вершины.
(314429) Парабола проходит через точки . Найдите координаты её вершины.
(314437) Парабола проходит через точки . Найдите координаты её вершины.
(314460) Парабола проходит через точки . Найдите координаты её вершины.
(314461) Парабола проходит через точки . Найдите координаты её вершины.
(314466) Парабола проходит через точки . Найдите координаты её вершины.
(314477) Парабола проходит через точки . Найдите координаты её вершины.
(314482) Парабола проходит через точки . Найдите координаты её вершины.
(314483) Парабола проходит через точки . Найдите координаты её вершины.
(314411) При каких значениях  вершины парабол
вершины парабол  и
и  расположены по разные стороны от оси
расположены по разные стороны от оси  ?
?
(314424) При каких значениях  вершины парабол
вершины парабол  и
и  расположены по разные стороны от оси
расположены по разные стороны от оси  ?
?
(314428) При каких значениях  вершины парабол
вершины парабол  и
и  расположены по разные стороны от оси
расположены по разные стороны от оси  ?
?
(314459) При каких значениях  вершины парабол
вершины парабол  и
и  расположены по одну сторону от оси
расположены по одну сторону от оси  ?
?
(314727) Известно, что графики функций  и
и  имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
(314728) Известно, что графики функций  и
и  имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
(314729) Известно, что графики функций  и
и  имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
(314730) Известно, что графики функций  и
и  имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
(314731) Известно, что графики функций  и
и  имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
(314732) Известно, что графики функций  и
и  имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
(314734) Известно, что графики функций  и
и  имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
(314736) Известно, что графики функций  и
и  имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
(314737) Известно, что графики функций  и
и  имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
(314738) Известно, что графики функций  и
и  имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
(314752) Известно, что графики функций  и
и  имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
ОТВЕТЫ
| № задачи | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ответ | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| № задачи | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| ответ | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| № задачи | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| ответ | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| № задачи | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 |
| ответ | 
| 
| 
| 
| 
| 
| 
| |
| № задачи | 39 | 40 | 41 | 42 | 42 | 43 | 44 | 45 |
| ответ | | | 
| 
| 
| 
| 
| 
|
| № задачи | 46 | 47 | 48 | 49 | 50 | 51 | 52 |
| ответ | 
| 
| 
| 
| 
| 
| 
|
7







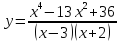 и определите, при каких значениях параметра
и определите, при каких значениях параметра 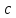 прямая
прямая 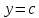 имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.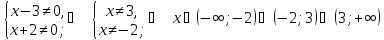 . Значит,
. Значит,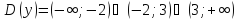 .
.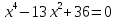
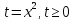
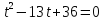
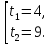
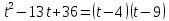 ,
, 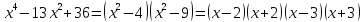 .
.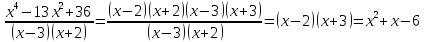 .
. 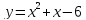 . Это квадратичная функция, графиком её является парабола с вершиной в точке
. Это квадратичная функция, графиком её является парабола с вершиной в точке 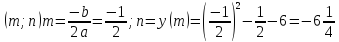 ; ветви направлены вверх, т.к.
; ветви направлены вверх, т.к. 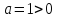 . График этой функции получается из графика функции
. График этой функции получается из графика функции 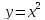 смещением вдоль оси Ох на
смещением вдоль оси Ох на 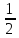 ед. отрезка вправо, и вдоль оси Оу на
ед. отрезка вправо, и вдоль оси Оу на 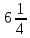 ед. отрезка вниз.
ед. отрезка вниз. 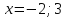 , то, для того, чтобы выколоть точки на графике, которые не удовлетворяют области определения, найдём ординаты этих точек:
, то, для того, чтобы выколоть точки на графике, которые не удовлетворяют области определения, найдём ординаты этих точек: 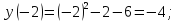
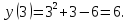
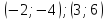 .
.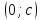 параллельно оси Ох, она будет пересекать параболу только в одной точке, если она проходит либо через вершину параболы, т.е.
параллельно оси Ох, она будет пересекать параболу только в одной точке, если она проходит либо через вершину параболы, т.е. 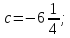 либо через выколотые точки, т.е.
либо через выколотые точки, т.е.