Замечательные линии треугольника

Обобщающий урок по теме:

«Замечательные линии треугольника (Медиана, биссектриса, высота)»

Тип урока: Урок систематизации знаний

Цель: Актуализация знаний по теме урока, используя материал 7- 9 классов. Повторить определения, свойства медианы, биссектрисы и высоты треугольника. В ходе урока проверить теорию и практические умения. Решить задачи, которые вызывают трудности, когда в условии встречаются данные понятия.

ХОД УРОКА

Сегодня у нас уже второй урок из цикла «Повторение», подготовки к ГИА. На первом уроке мы повторили формулы, которые используются для нахождения площади треугольника.

Сегодня мы вновь говорим о треугольнике. Почему именно о нем? Ну во - первых потому, что это одна из основных фигур геометрии, а во-вторых, закончив в 9 классе планиметрию, мы, в 10,11, классах при решении стереометрических задач неоднократно будем обращаться к решению треугольников.

Сегодня наш урок будет посвящен некоторым замечательным линиям треугольника - таким понятиям, как медиана, биссектриса и высота. Почему именно им? Да потому, что опыт показывает, что когда эти понятия встречаются в задачах, ученик, в лучшем случае, может вспомнить определение, построить их, но этого бывает крайне недостаточно, для решения задачи.

Поэтому цель нашего урока - систематизировать ваши знания по данной теме. Всё, о чём мы сегодня будем говорить, вы изучали в 7, 8 , начале 9 класса. Какие-то свойства вспомним, новые - докажем.

Итак, давайте вспомним основные определения, которые нам сегодня понадобятся.

- дайте определение треугольника. (Почему точки не должны лежать на одной прямой?);

- неравенство треугольника;

- классификация треугольника по сторонам и углам;

- как, зная стороны треугольника определить его вид (следствие из теоремы косинусов);

- сформулируйте свойства диагоналей параллелограмма (следствие из теоремы косинусов);

- Какие формулы для вычисления площади треугольника вы знаете?

Ну, а теперь главные герои нашего урока

- что такое медиана треугольника;

- какие ещё ассоциации у вас вызывает это понятие?

*В треугольнике можно провести три медианы

* Все три медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.

* В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна её половине.

И обратная теорема: если в треугольнике одна из медиан равна половине стороны, к которой она проведена, то этот треугольник прямоугольный.

* В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна радиусу описанной около треугольника окружности.

* Медиана, проведенная к основанию равнобедренного треугольника, является биссектрисой и высотой.

*Часто при решении задач, в которых упоминается медиана треугольника надо сделать дополнительное построение: удвоить медиану треугольника для того, чтобы достроить треугольник до параллелограмма, а затем применить свойство диагоналей параллелограмма: Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

Давайте посмотрим, как применяются названные вами свойства при решении задач.

Решение задач № 1,2,5 из приложения «Медиана»

Кроме названых Вами, есть ещё несколько замечательных свойств:

Медиана не только делит сторону треугольника. На две равные части, она делит треугольник на два равновеликих треугольника.

Решение задачи № 3 из приложения «Медиана»

Кроме того, того, три медианы треугольника делят его на 6 равновеликих треугольника (Делят его площадь на 6 равных частей)

Этот факт мы запомним и примем без доказательства.

Решим такую задачу:

Решение задачи № 4 из приложения «Медиана».

Вторая главная героиня нашего урока - биссектриса.

1.Дайте определение биссектрисы угла и биссектрисы треугольника. Чем они отличаются?

2.Сколько биссектрис можно провести в треугольнике? Всегда ли они пересекаются в одной точке? Как она называется? (Инцентр)

3.Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник. (Вспомнить формулы)

4. Если из одной вершины треугольника провести медиану, биссектрису и высоту, то биссектриса будет лежать между медианой и высотой треугольника.

5. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

6. Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.

Это свойство применяется при решении задач достаточно часто.

Решение задачи №1 из приложения «Биссектриса, высота».

Так же как ив случае с медианой зададимся вопросом: «КАК относятся площади полученных треугольников»?

Решение задачи №2 из приложения «Биссектриса, высота».

РЕЗЕРВ-

Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла. (С доказательством).

Ну и последняя на сегодня замечательная линия треугольника – высота.

Итак, высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.

• Всегда ли точка пересечения высот лежит внутри треугольника?

• Как наз. Эта точка? (ортоцентр);

• В какой точке пересекаются все высоты прямоугольного треугольника?

• Решение задачи №3 из приложения «Биссектриса, высота». (Обсудить вид треугольника.)

Как только мы опускаем высоту, у нас тут же образуется прямоугольный треугольник. Поэтому естественным будет вспомнить все основные формулы, связанные с прямоугольным треугольником.

(К доске вызываются 2 человека и записывают всевозможные формулы, связанные с прямоугольным треугольником.)

Итак, сегодня на уроке мы с вами вспомнили старые и изучили несколько новых свойств медианы, биссектрисы и высоты. У вас на столах, на отдельных листах собран весь сегодняшний теоретический материал, к которому вы сможете время от времени обращаться. Все эти формулы, теоремы Вы должны полюбить, сделать их своими помощниками. Потому что они очень часто необходимы при решении задач, но, к сожалению, не всегда находятся на первом уровне памяти.

Ну, а чтобы научиться применять их- здесь совет скорее философский: хочешь научиться решать геометрические задачи -решай их. Поэтому домашнее задание следующее: у вас на столах листы с задачами на отработку сегодняшних навыков. (Приложение дом задание) Время на решение-2 недели. Вы сдаёте решения, защищая их. В Течении этих 2 недель Вы можете задавать мне любые вопросы по решению. Спасибо за урок.

Приложение «Биссектриса, высота треугольника»

1. Отрезок CD – биссектриса треугольника АВС, АС=12 см, ВС= 18 см, AD=10 см. Найдите BD.

2. Биссектриса делит треугольник на два, площади которых относятся как заключающие её стороны. 

3. Найдите высоту треугольника со сторонами 2 см, 4 см, 5 см. Сделайте рисунок.

Приложение «Медиана треугольника»

1.

2.

3.

4.

Дано:

ABC – равносторонний

AK, BP, CM – медианы

OK=2 см

Найти:

BP - ?

Дано:

АВС(АВ=ВС);

АК, ВР, СМ- медианы

АК=СМ=15 см; ВР=10 см

Найти:

S ABC

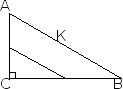
Дано:

ABC (C=90 )

СК - медиана

АС=9см; ВС = 12см

Найти: СК

Дано:

АВС

ВМ - медиана

Доказать:

S АВМ = S ВМС

5. В треугольнике ABC проведены медианы BK, AO, CN, пересекающиеся в точке D. Площадь треугольника AND равна 4 см2 . Найти площадь треугольника ABC.

6. Боковая сторона равнобедренного треугольника 8 см, а медиана, проведенная к ней, - б см. Найдите основание треугольника.

Приложение №3

Домашнее задание

1.На медиане ВМ равнобедренного треугольника АВС с основанием АС отметили точку О. Докажите, что треугольник АОС - равнобедренный.

2. Медианы СА, КВ, ОН равнобедренного треугольника ОСК (СО=ОК) пересекаются в точке Е. Отрезок ЕА= 6 см. Найдите длину медианы КВ.

3. Медиана, проведенная к гипотенузе прямоугольного треугольника, делит прямой угол в отношении 1:2 и равна 16 см. Вычислите стороны треугольника. (Вспомните: 1) зависимость между гипотенузой и медианой, проведенной к ней; 2) признак равнобедренного треугольника; 3) следствие из теоремы Пифагора).

4. Определите вид треугольника, сделайте его эскиз и проведите в нём высоты:

а) 5 см, 12 см, 1 3см. б) 13 см, 14 см, 15 см. в) 6 см, 10 см, 12 см.

5. Стороны треугольника равны 7 см, 11 см, 12 см. Найдите медиану треугольника, проведённую к его большей стороне.

6. Отрезок АК – биссектриса треугольника АВС, АВ=12 см, ВК= 8 см,

СК = 18 см. Найдите АС.

7. В треугольнике АВС проведена биссектриса АК. АВ= 12 см, АС = 15 см. Найдите отношение площадей треугольников АВК и АКС.

8.Стороны треугольника равны 29 см, 25 см и 6 см. Найдите высоту, проведенную к меньшей стороне.

9.В прямоугольном треугольнике высота, проведенная к гипотенузе, делит её на отрезки 16см и 9 см. Найдите периметр треугольника.

10.Две стороны треугольника равны 13 см и 15 см, а высота, проведенная к третьей стороне- 12 см. Найдите медиану треугольника, проведенную к третьей стороне.