Презентация к уроку геометрии "Треугольники"

Треугольники

Виды треугольников:

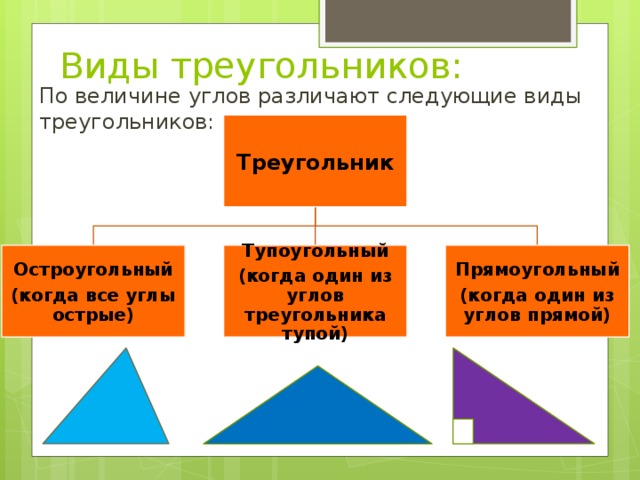
По величине углов различают следующие виды треугольников:

Треугольник

Прямоугольный

Остроугольный

Тупоугольный

(когда один из углов прямой)

(когда все углы острые)

(когда один из углов треугольника тупой)

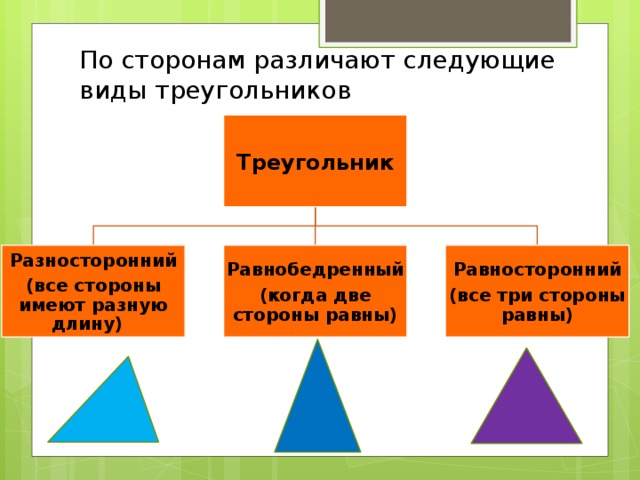
По сторонам различают следующие виды треугольников

Треугольник

Разносторонний

Равнобедренный

Равносторонний

(все стороны имеют разную длину)

(когда две стороны равны)

(все три стороны равны)

ГИПОТЕНУЗА

КАТЕТ

Прямоугольный треугольник

А

Треугольник называется прямоугольным , если один из его углов равен 90.

Сторона, лежащая против угла 90, называется гипотенузой . Две другие стороны – катетами .

90

КАТЕТ

С

В

Теорема Пифагора

А

ТЕОРЕМА:

Квадрат гипотенузы, равен сумме квадратов катетов.

АВ² = АС² + СВ²

С

В

БОКОВАЯ СТОРОНА

БОКОВАЯ СТОРОНА

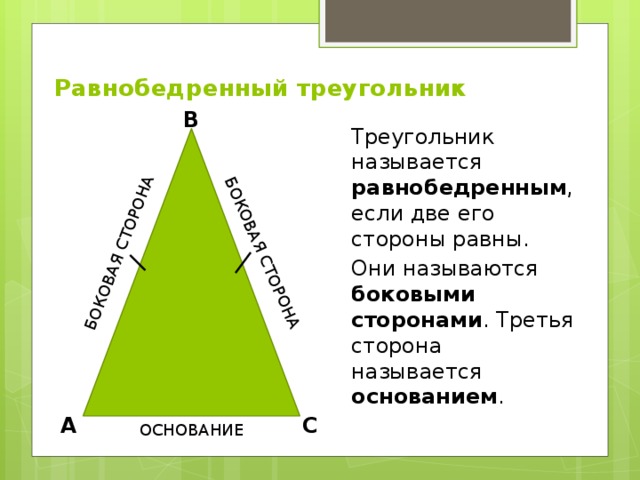
Равнобедренный треугольник

В

Треугольник называется равнобедренным , если две его стороны равны.

Они называются боковыми сторонами . Третья сторона называется основанием .

А

С

ОСНОВАНИЕ

В

В равнобедренном треугольнике углы, прилежащие к основанию, равны, а высота, медиана и биссектриса, проведенные к основанию – совпадают.

ВН является одновременно и медианой, и высотой. И биссектрисой.

А

С

В

Обратное свойство:

Если в треугольнике два угла равны. То этот треугольник равнобедренный

А

С

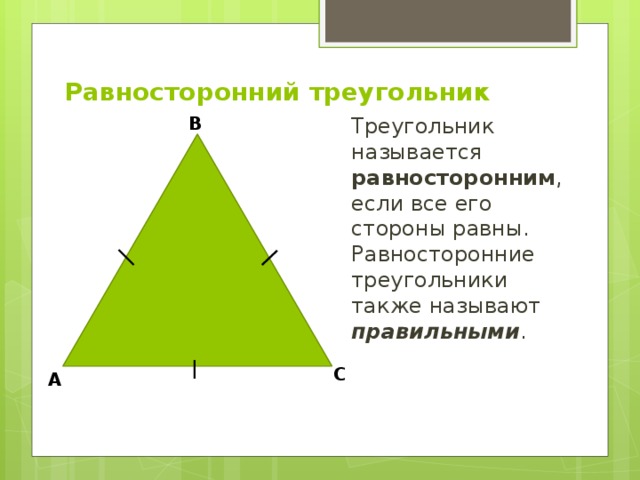
Равносторонний треугольник

В

Треугольник называется равносторонним , если все его стороны равны. Равносторонние треугольники также называют правильными .

С

А

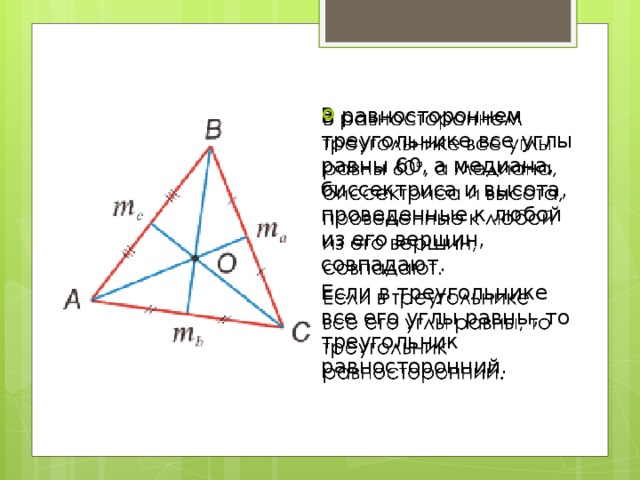
В равностороннем треугольнике все углы равны 60, а медиана, биссектриса и высота, проведенные к любой из его вершин, совпадают.

Если в треугольнике все его углы равны, то треугольник равносторонний.

Равенство треугольников

Равные треугольники – это такие треугольники, которые можно совместить друг с другом, наложив друг на друга так, чтобы они совпадали.

Признаки равенства треугольников

1 признак . По двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

В

В

1

А

С

А

С

1

1

Признаки равенства треугольников

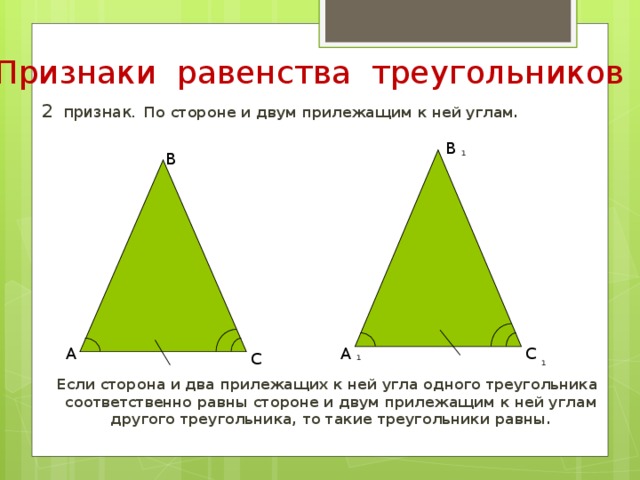
2 признак. По стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

В

1

В

А

А

С

С

1

1

Признаки равенства треугольников

3 признак. По трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

В

В

1

А

С

С

А

1

1

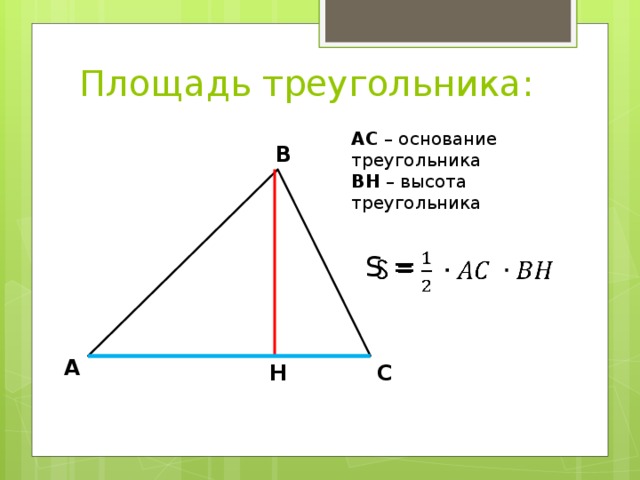
Площадь треугольника:

АС – основание треугольника

ВН – высота треугольника

В

S =

А

С

Н

А

Площадь прямоугольного треугольника равна половине произведения катетов.

S =

В

С

Задачи:

• Найдите площадь треугольника, изображённого на рисунке.

Решение:

• По теореме Пифагора найдем катет СВ

АВ² = АС² + СВ²

СВ = АВ² - АС²

СВ² = 5² - 3²

СВ² = 25 – 9

СВ² = 16

СВ = 4

2) S =

S =

Ответ: S = 6.

А

5

3

С

В