5
Сабактын планы
Алгебра 9-класс
Сабактын темасы: Геометриялык прогрессиянын
касиеттери
Сабактын тиби: Жаңы материалды өздөштүрүү
Колдонулуучу усулдар: Жеке иштөө, жупта иштөө
Колдонулган баалоо усулдары: өзүн-өзү баалоо, бири-бирин баалоо
Жабдылышы/каражаттар: тапшырмалардын даярдалган тексттери
Сабактын максаты: окуучулардын ой-жүгүртүүлөрүн өстүрүү
үчүн төмөндүдөй шарттарды түзүү
Окуу материалынын мазмуну аркылуу интеллектуалдык маданиятын өстүрүү б.а. эсептерди чыгарууда ык-навыктарды, билимдерди жана билгичтиктерди колдонуу
Сабакта иштөө мезгилинде өзүн-өзү баалоо жана контролдой алуу маданиятына ээ болуу.
Коммуникативдик маданиятына б.а. математикалык сүйлөө речин өстүрүү, бири-бири менен мамиле түзүү, өз оюн айта билүү жана бирөөнүкүн уга билүү, ишти анализдөө жана жыйынтык чыгара билүүгө ээ болуу.
САБАКТЫН ЖΥРΥШΥ:
Балдар! Төмөндөгү сүйлөмдү аягына чыгаргыла:
« Жолду баскан арбытат (жеңет), ал эми математиканы ой жүгүртө алган адам.»
« Дорогу осилит идущий, а математику …мыслящий.»
Суроо: Прогрессия деген сөздү кандай түшүнөсүңөр?
Мугалим: прогрессия деген сөз латын тилинен которгондо алдыга жылуу дегенди тγшγндγрөт.
Силердин ой-жүгүртүүңөрдү белгилөө үчүн өзүн-өзү баалоо баракчасын толтурасыңар, мында ар-бир тапшырма үчүн өзүңөргө балл коёсуңар.
Билимдерди актуалдаштыруу .
Көңүл бургула!
1-тапшырма( 5 балл). Доскада сан удаалаштыктары жазылган:
2, 4, 6, 8, …;
1, 2, 4, 8, 16,….;
2, 22, 23, 24,…;
2, 2, 2, 2, …;

6) 
7) 2,  2,
2, 
Аларды группаларга бөлгүлө. Жоопторду таблица көрүнүшүндө көрсөткүлө:
| 1-группа | 2-группа | 3-группа |
| Арифметикалык прогрессия | Геометриялык прогрессия | Арифметикалык да, геометриялык да прогрессия эмес |
|
|
|
|
Жоопторду анализдөө аркылуу балдар арифметикалык жана геометриялык прогрессиялардын аныктамаларын кайталашат.
Жооп:
| 1-группа | 2-группа | 3-группа |
| Арифметикалык прогрессия | Геометриялык прогрессия | Арифметикалык да, геометриялык да прогрессия эмес |
| 1), 4), 5); | 2), 3), 4), 6); | 7) |
2. Жаңы билимди өздөштүрүү
1-теорема. Геометриялык прогрессиянын биринчи мүчөсүнөн башка ар бир мүчөсүнүн квадраты аны менен коңшулаш эки мүчөсүнүн көбөйтүндүсүнө барабар, б.а.
 мында
мында  (1)
(1)
 (2)
(2)
1-маселе. Эгер 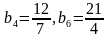 болсо, анда геометриялык прогрессиянын оң мааниге ээ болгон бешинчи мүчөсүн тапкыла.
болсо, анда геометриялык прогрессиянын оң мааниге ээ болгон бешинчи мүчөсүн тапкыла.
1-теорема боюнча 
3. Теманы бышыктоо мисалдарын иштөө
Окуу китебинин 78-бетиндеги 70-көнүгүү.
Эгер а) 
Болсо, анда геометриялык прогрессиянын оң мааниге ээ болгон алгачкы беш мүчөсүн жазгыла.
Чыгаруу:
а) ГПнын экинчи мүчөсүн таап, андан кийин бөлүмүн аныктайбыз. Кийин төртүнчү жана бешинчи мүчөлөрүн таап алабыз.
(1) формула боюнча:

же (2) формула боюнча

Геометриялык прогрессиянын бөлүмү  экендиги келип чыгат.
экендиги келип чыгат.


Эми прогрессиянын мүчөлөрүн тизе турган болсок, ал мындайча болот.
Жогорудагы мисалды иштөөдө бөлүмүн таап алгандан кийин, геометриялык прогрессиянын n-мүчөсүнүн формуласын колдонсок да ыңгайлуу болот.
Ушул мисалдын б) бөлүгүн туура иштегендерге 5 балл.

1-теорема боюнча 2-формуланы колдонсок,

Эми ГПнын бөлүмүн тапсак:


Жооп:
71-көнүгүү. а)  б)
б) 
болсо, анда мүчөлөрү оң мааниге ээ болгон геометриялык прогрессиянын жетинчи мүчөсүн жана бөлүмүн жазгыла.
Жогорудагыдай эле иштейбиз. (5балл)
а)
Жообу: 
б)
Жообу: 
73-көнүгүү: (5 балл)
а)
, жообу: 
б)
, жообу: 
в) -7, х, -28
жообу: 
г) -6, х, -54
, жообу: 
д) 2, х, 16
, жообу: 
е) -1, х, -1
 жообу:
жообу: 
4. Жооптордун анализи.
5. Сабакты жыйынтыктайбыз. Баалоо баркчасына баллдарды коебуз.
Эгер силер 20 балл топтосоңор «5» деген бааны коёсуңар.
Эгер 15 баллдын тегерегинде балл топтосоңор «4» деген бааны коесуңар
10 дун тегергинде балл алсаңар, «3» деген бааны коёсуңар.
6. Υй тапшырмасын дайындоо.
1) Окуу китебинин 78-бетиндеги 72, 74-көнүгүүлөр
2) Арифметикалык прогрессия темаын бүт бойдон, геометриялык прогрессия темасын касиеттерин кошуп кайталоо.
3) «Прогрессия» деген сөзгө кроссворд түзүп келүү









 2,
2, 
 мында
мында  (1)
(1) (2)
(2)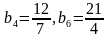 болсо, анда геометриялык прогрессиянын оң мааниге ээ болгон бешинчи мүчөсүн тапкыла.
болсо, анда геометриялык прогрессиянын оң мааниге ээ болгон бешинчи мүчөсүн тапкыла.



 экендиги келип чыгат.
экендиги келип чыгат.





















