Муниципальное бюджетное общеобразовательное учреждение лицей №1 г. Пролетарска Ростовской области
Проект по теме:
«Сложные проценты в нашей жизни»
Выполнил: ученица 10А класса Шкодин Дмитрий
Руководитель: Величко Елена Владимировна
Учитель: алгебры, геометрии
г. Пролетарск, 2024
Оглавление:
| 1. | Введение………………………………………………………………... | 3 |
| 2. | Основная часть: |
|
| 2.1 | История возникновения процентов …………………………………… | 5 |
| 2.2 | Понятие «сложные проценты» ………….……………………………. | 6 |
| 2.3 | Формула простых процентов ……….………………………………... | 8 |
| 2.4 | Формула сложных процентов…………………..…………………….. | 9 |
| 2.5. | Исследование банковских вкладов ………………………………….. | 10 |
| 2.6. | Практическая часть…………………………………………………… | 11 |
| 3. | Заключение…………………………………………………………….. | 13 |
| 4. | Интернет ресурсы…………………...………………………………… | 14
|
5. Приложение …………………………………………………………… 15
1. Введение:
Сложные проценты окружают нас в современной жизни, и в большей степени распространены в таких глобальных структурах, как банковская. В настоящее время банковская система играет значительную роль в экономике нашей страны. Процентные вычисления представляют интерес не только для будущих финансистов, но и для каждого человека.
Многие жизненные ситуации требуют знания вычисления процентов:
Получение кредитов в банке;
Расчёт налогов с заработной платы
Расчёт компенсации по коммунальным платежам
Банковские вклады;
Покупка товара в кредит;
Аналитические данные
Из многих жизненных ситуаций я выбрал банковские вклады в качестве применения сложных процентов. Недавно в педагогический коллектив приходил сотрудник сбербанка, которая рассказала о взносах и вложениях под проценты, придя в класс классный руководитель рассказал нам, и мы стали просчитывать выгодно ли это человеку. Меня заинтересовал этот вопрос, и я решил посвятить свой проект данной теме. Новизна исследования состоит в том, что в работе рассматриваются сведения,
которые не изучаются в школьном курсе математики, и обобщается на только на местном материале.
Цели проекта:
Изучить сложные проценты в повседневной жизни человека
Сформировать понимание необходимости знаний процентных вычислений для решения большого круга задач
Научиться применять знания о процентах в повседневной жизни;
Задачи проекта:
Рассмотреть понятие сложных процентов;
Научиться решать задачи на сложные проценты;
Показать, что формула сложных процентов – это ни что иное, какие геометрическая прогрессия;
Провести исследование трёх (сбербанк, Т банк, втб) банков и сделать вывод, куда наиболее выгодно вкладывать деньги.
Почему я решил выбрать именно эту тему для своего проекта
Прежде всего мой выбор зависел от актуальности или востребованности данной темы.
Простые и сложные проценты окружают нас всюду, но мы зачастую об этом даже не задумываемся. Сложные проценты встречаются в банковских системах. Многие жизненные ситуации требуют знания вычисления процентов, такие как открытие банковских вкладов и получения кредитов. Также я буду взаимодействовать со сложными процентами в ходе изучения своей специальности. Именно поэтому я выбрала эту тему для своего изучения и представления своим сверстникам.
Объект исследования: сложные проценты
Предмет исследования: применение сложных процентов в реальной жизни.
Мой двоюродный брат Влад уже делал проект на подобную тему в 11 классе: «Налоги и заработная плата», где определил, как выполняются выплаты налогов на разных предприятиях. Я решил продолжить работу над процентами и кредитами, но на этот раз я решил рассмотреть, какой банк наиболее выгоден и куда лучше вкладывать деньги. Также, работа с процентами встречается в задаче номер 17 в ЕГЭ по профильной математике. Поэтому, я считаю, что данная тема будет актуальна также и среди будущих или нынешних одиннадцатиклассников.
Основная часть
История возникновения процентов:
Перед началом своей работы я бы хотел дать определение, что такое проценты, на просторах интернета и из учебников алгебры, физики, химии я нашёл следующую информацию.
Нейро сеть – говорит о том, что процент — это одна сотая часть числа или какой-либо величины. Слово «процент» происходит от латинского pro centum, что означает «на сто». После числа вместо слова «процент» ставят знак %.
Wiki страничка утверждает, что Проце́нт (от лат. per centum «на сотню; сотая») — одна сотая часть; обозначается знаком «%»; используется для обозначения доли чего-либо по отношению к целому. Например, 17 % от 500 кг означает 17 частей по 5 кг каждая, то есть 85 кг. Справедливо также утверждение, что 200 % от 500 кг является 1000 кг, поскольку 1 % от 500 кг равен 5 кг, и 5 × 200 = 1000.
В учебнике алгебры проценты в алгебре — это часть целого, выраженная в сотых долях. 1 процент (1%) равен 1/100 (или 0,01) от целого числа.
В учебники физики понятие «процент» используется при определении коэффициента полезного действия (КПД), точности измерительных приборов, при записи каких-либо результатов, определении влажности воздуха
В учебники химии процентная концентрация— это массовая доля, выраженная в процентах. Она показывает, сколько граммов растворённого вещества содержится в 100 граммах раствора.
Исходя из полученных данных, я обобщил и получил утверждение, что проценты – одно из математических понятий, которые часто встречаются в повседневной жизни.
Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян, которые пользовались шестидесятеричными дробями. Уже в клинописных таблицах вавилонян содержатся задачи на расчет процентов. До нас дошли составленные вавилонянами таблицы процентов, которые позволяли быстро определить сумму процентных денег. Были известны проценты и в Индии.
Индийские математики вычисляли проценты, применив так называемое тройное правило, т. е. пользуясь пропорцией. Они умели производить и более сложные вычисления с применением процентов. Денежные расчеты с процентами были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. Даже римский сенат вынужден был установить максимально допустимый процент, взимаемый с должника, так как некоторые заимодавцы усердствовали в получении процентных денег. От римлян проценты перешли к другим народам.
В средние века в Европе в связи с широким развитием торговли особо много внимания обращали на умение вычислять проценты. В то время приходилось рассчитывать не только проценты, но и проценты с процентов, т. е. сложные проценты, как называют их в наше время. Отдельные конторы и предприятия для облегчения труда при вычислениях процентов разрабатывали свои особые таблицы, которые составляли коммерческий секрет фирмы.
Впервые опубликовал таблицы для расчета процентов в 1584 году Симон Стевин – инженер из города Брюгге (Нидерланды). Стевин известен замечательным разнообразием научных открытий в том числе – особой записи десятичных дробей.
Долгое время под процентами понимались исключительно прибыль и убыток на каждые 100 рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике. Нынче процент – это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу)
Понятия «простые проценты» и «сложные проценты»:
Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада (долга).
Простыми процентами можно считать вклад (долг) только в том случае, если происходит однократная выплата процентов и всей суммы вклада (долга) одновременно, при этом полностью отсутствует возможность досрочной частичной или полной выплаты вклада (долга) и/или полностью отсутствует возможность продления вклада (долга).
При досрочной выплате процентов происходит увеличение суммы вклада (долга), значит первоначальная сумма вклада (долга) изменилась, следовательно, применение простых процентов в этом случае бессмысленно, поскольку это уже не простые проценты, а сложные.
Сложные проценты – форма расчета дохода, основанная на присоединении к сумме долга начисленных, но невыплаченных процентов, начисление процентов на проценты, расчет процентов на два или большее число периодов, проводимый таким образом, что процент начисляется не только на исходную сумму, но и на процент, начисленный в предыдущем периоде. При расчетах применяют сложные дискретные проценты, начисляемые за фиксированные интервалы времени.
В истории есть немало примеров, доказывающих магическую силу сложных процентов. Например, можно вспомнить о примечательном поступке.
Бенджамина Франклина. Франклин, который умер в 1790 году, завещал по $5 000 долларов двум своим любимым городам, Бостону и Филадельфии.
По условию завещания города могли получить эти деньги в два приема, через 100 и 200 лет после вступления завещания в силу. Через 100 лет каждый город мог взять для финансирования общественных работ по $500 000, а еще через 100 лет – все деньги со счета.
Через 200 лет, в 1990 году, города получили примерно по $20 000 000. Франклин очень наглядно показал, выгоду сложных процентов.
Для начисления процентов по вкладам (депозитам) и кредитам, применяются следующие формулы процентов:
Представьте себе, что вы открыли в банке вклад в сумме а р. под р% годовых на t лет. У вас есть две стратегии поведения: либо в конце каждого года хранения вклада снимать проценты по вкладу, т. е. полученную прибыль
 в размере
в размере
∗ 𝑎рублей, либо прийти в банк один раз — в конце срока хранения вклада. Какой доход вы получите в том и другом случая
Формула простых процентов:
 В первом случае при t = 1 вы получите (𝑎 + 𝑝
В первом случае при t = 1 вы получите (𝑎 + 𝑝
100
∗ 𝑎) рублей, при t = 2 ваша
 итоговая сумма составит (𝑎 + 2𝑝
итоговая сумма составит (𝑎 + 2𝑝
100
∗ 𝑎) рублей, при t = 3 – (𝑎 + 3𝑝
 100
100
∗ 𝑎) рублей
и т. д. Математическая модель ситуации — конечная арифметическая прогрессия
 𝑎, 𝑎 + 𝑝 100
𝑎, 𝑎 + 𝑝 100
∗ 𝑎, 𝑎 + 2𝑝
 100
100
∗ 𝑎, 𝑎 + 3𝑝
 100
100
∗ 𝑎, … , 𝑎 + 𝑡𝑝
 100
100
∗ 𝑎.
 Итак, при первой стратегии поведения за t лет вы получите𝑎 (1 + 𝑡𝑝 ) р. —
Итак, при первой стратегии поведения за t лет вы получите𝑎 (1 + 𝑡𝑝 ) р. —
100
это так называемая фopмyла простых процентов.
Формула сложных процентов:
Сложный процент — это процент, который начисляется на начальную сумму вложений, а также на проценты, накопленные за предыдущие периоды. Начисление сложных процентов предполагает реинвестирование полученного дохода.
Где используется сложный процент:
В инвестициях. Полученную прибыль (дивиденды по акциям, купоны по облигациям или доход от перепродажи подорожавших ценных бумаг) инвестор не выводит с брокерского счёта, а реинвестирует в те же или другие ценные бумаги, что приводит к росту конечной прибыли.
В банковских вкладах и накопительных счетах. Если не снимать со счёта выплаченные проценты, то денег после начисления становится больше, поэтому в следующую выплату процент будет рассчитан на новую сумму.
Формула для расчёта сложных процентов выглядит следующим образом:
SUM = X * (1 + %)n, где:
SUM — конечная сумма;
X — начальная сумма;
% — процентная ставка, процентов годовых / 100;
n — количество периодов, лет (месяцев, кварталов).
Ещё одна формула для расчёта сложных процентов:
Σ = I * (1 + s * t / d * 100%) (в степени n), где:
Σ — будущая сумма на счету;
I — начальная сумма вложений;
s — процентная ставка;
t — число дней, через который начисляется процентный доход;
d — число дней в году;
n — число периодов выплаты процентов.
Сложный процент работает следующим образом: вы не тратите полученную прибавку, а добавляете её к общей сумме и начинаете получать дополнительный прирост на эту часть.
Исследование банковских вкладов:
Банковский вклад (или банковский депозит) — сумма денег, переданная лицом кредитному учреждению с целью получить доход в виде процентов, образующихся в ходе финансовых операций с вкладом.
Обычно банки предлагают простое начисление процентов. Что это значит? Это значит, что проценты будут начислены на ваш вклад только в конце срока. Т.е. допустим вы открыли вклад под 17 % годовых на срок 2 года и вложили 300 000 рублей. Через год вам будет начислено в виде процентов 51 000 рублей. Если вы оставите вклад на второй год, то по истечении этого срока вам будет начислена еще 51 000 рублей. За 2 года, при простом начислении процентов ваша итоговая сумма составит: 102 000 рублей.
Если бы было сложное начисление процентов, то картина немного меняется. Через 1 год, на вашем счету также было бы 351 000 рублей (300 000 — ваш вклад + 51 000 рублей в виде процентов). Однако, эта начисленная тысяча, в конце первого периода присоединилась бы к основному телу депозиту. И все проценты уже начислялись бы на эту общую сумму. Т.е. вы на второй год получили бы 17 %, только уже не с 300 000 рублей, а с 351 тысячи рублей. В деньгах это получается — 59 670 рублей. Итого, за 2 года при сложном начислении ваша сумма составит: 410 670 рублей/
Я решил провести исследование, в какой из банков выгоднее вкладывать деньги. Для этого я рассмотрел 3 банка: Сбербанк, ВТБ, Т банк
Первоначальная сумма нам неизвестна, срок – 5 лет, итоговая сумма 3000000 рублей. Начисление процентов– ежегодное.
Задача.
В следующем году я заканчиваю школу и у меня цель поступать в один из ВУЗов г. Ростов-на-Дону. Уже сейчас родители планируют приобрести мне собственную квартиру. Можно рассмотреть следующие варианты: приобретение вторичного жилья, квартира в новостройке или в строящемся доме. Стоимость жилья значительно отличается, поэтому мои родители выбирают самый выгодный вариант – приобретение жилья в новостройке. C 1 июля 2024 года принципиально трансформируется схема продаж жилья в строящихся домах: деньги дольщиков будут храниться в банке до ввода жилого комплекса в эксплуатацию. В конце прошлого года власти придумали новую схему финансирования жилищного строительства. Теперь девелоперы будут строить новое жилье только на кредиты банков или собственные деньги. Получать средства покупателей напрямую им нельзя.
Однако это не значит, что россияне потеряют возможность приобрести квартиру в строящемся доме, покупатель сможет выбрать понравившийся объект и заключить договор с застройщиком, но расплачиваться будет не с ним напрямую, а через банк, который выдал кредит на строительство.
Родители планируют приобрести квартиру в строящемся доме фирмы «N». Я решил рассчитать, какую сумму нужно вложить в банк под 24% годовых, чтобы купить эту квартиру, если дом строится 5 лет, а стоимость квартиры по договору составляет 3 млн рублей?
Так как в практической жизни используются простые проценты, а
задачи ЕГЭ решаются по формуле сложных процентов, то я провела расчеты по обеим формулам.
По формуле простых процентов сумма, которую нужно вложить в банк для того, чтобы по истечению 5 лет получить 3 млн рублей, составляет:
СБЕРБАНК
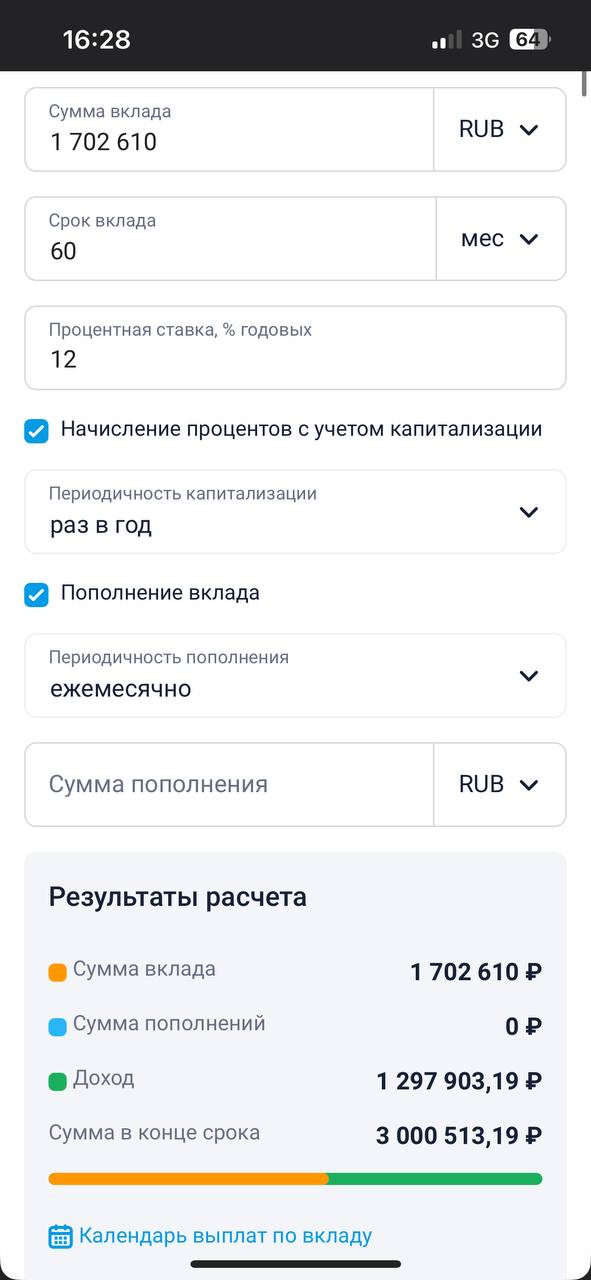
Вклад «Лучший %» (Приложение №1)
x рублей – первоначальный взнос
𝑡=5 лет
𝑝max = 12 %
Проводим вычисление по формуле нахождения сложных процентов:
S = x* (1+p/100)n
3000000 = x (1+0.12)5
X=3000000/(1.12)5
X= 1702610.7
ВТБ
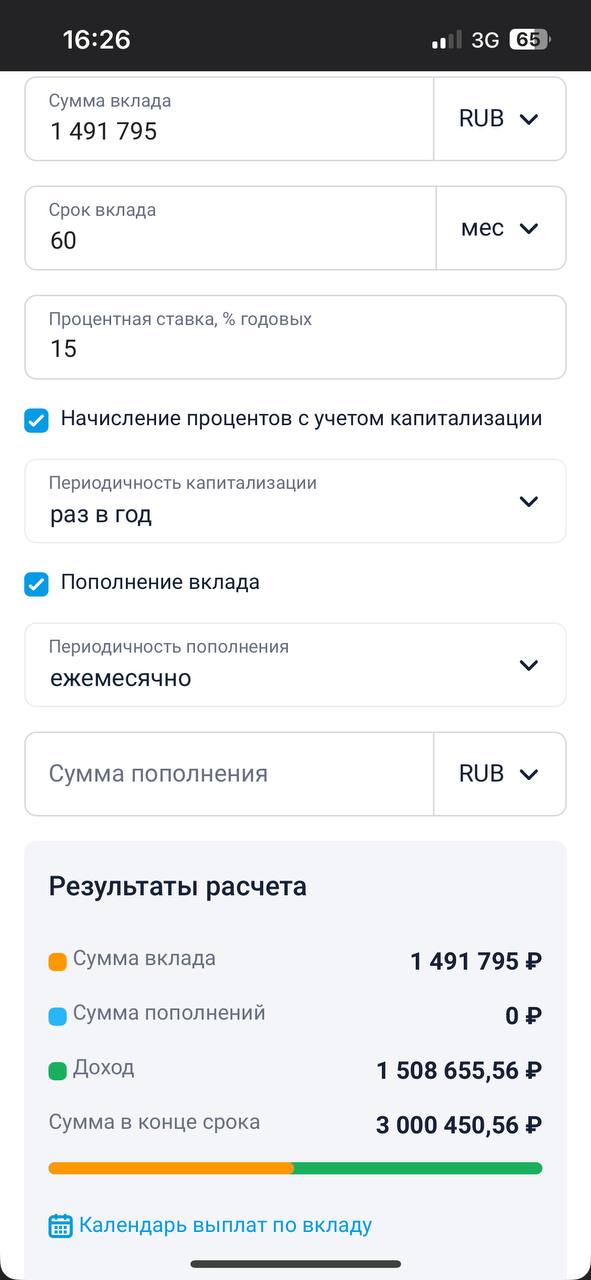
Вклад «ВТБ вклад» (Приложение №2)
x рублей – первоначальный взнос
𝑡=5 лет
𝑝max = 15 %
Проводим вычисление по формуле нахождения сложных процентов:
S = x* (1+p/100)n
3000000 = x (1+0.15)5
x=3000000/(1.15)5
x= 1491795
Т Банк
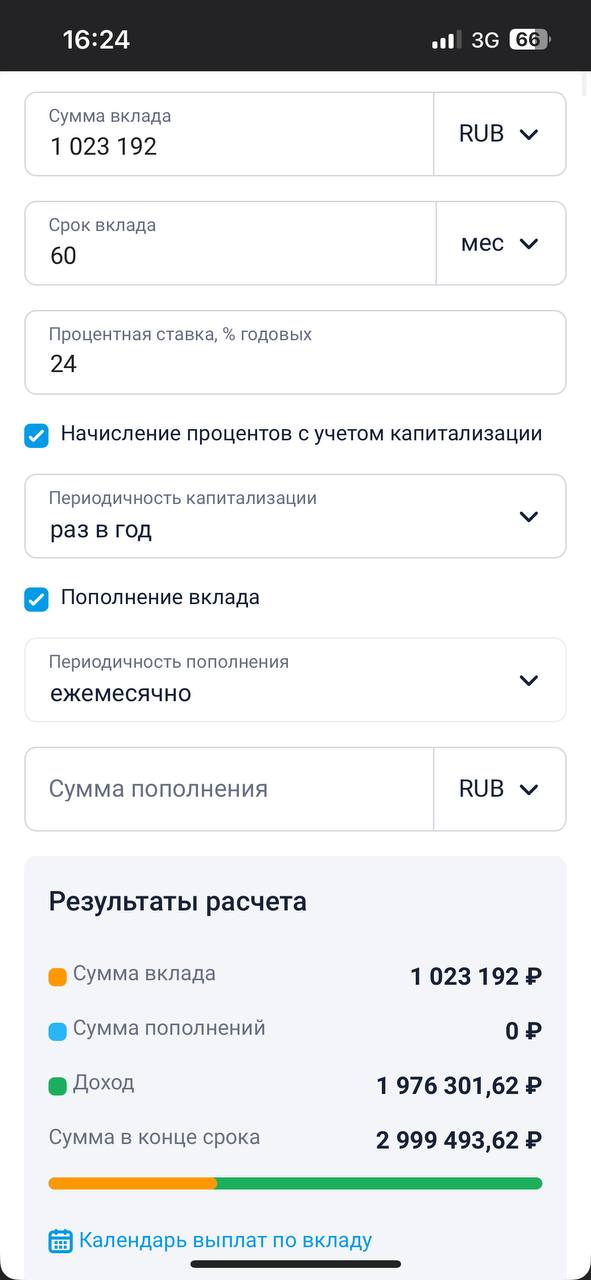
Вклад «Смарт вклад» (Приложение №3)
x рублей – первоначальный взнос
𝑡=5 лет
𝑝max = 24 %
Проводим вычисление по формуле нахождения сложных процентов:
S = x* (1+p/100)n
3000000 = x (1+0.24)5
x=3000000/ (1.24)5
x= 1023192
Заключение:
В процессе работы я исследовал простые и сложные проценты, а именно, рассмотрел понятие сложных процентов, провел анализ вкладов трёх известных банков, научился решать задачи на сложные проценты. Таким образом, цель моей работы достигнута.
Данная работа несёт за собой значительную практическую значимость, которая в будущем поможет более разумно размещать свои средства. Данный проект могу рекомендовать учащимся 9-11 классов на математических кружках и занятиях по подготовке к ЕГЭ с целью подготовки к экзаменам, при решении задач на проценты. А так же данная работа облегчит вкладчикам поиск более выгодных условий для вложения своих временно свободных средств, поможет разобраться в непростых финансовых механизмах и выбрать для себя оптимальную стратегию управления собственными денежными средствами.
Интернет-ресурсы и литература:
Ш.М. Алимов «Алгебра и начала математического анализа.. Учебник.»
https://damoney.ru/finance/slozniy-procent.php
https://www.sberbank.ru/ru/person
https://www.vtb.ru/
https://www.pochtabank.ru/
https://www.rshb.ru/
https://www.sovcombank.ru/
http://irynaprocent.blogspot.com/p/blog-page_29.html
Приложение №1
Калькулятор доходности вкладов
Приложение №2
Калькулятор доходности вкладов
Приложение №3
Калькулятор доходности вкладов







 в размере
в размере  𝑎, 𝑎 + 𝑝 100
𝑎, 𝑎 + 𝑝 100












