

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Максимумы, минимумы функций (для ДО)
Тема: Максимумы, минимумы функций
1. Изучить весь предложенный теоритический материал по данной теме и записать в тетрадь.
2. Рассмотреть пример 1,2 и записать в тетрадь.
3. Решить самостоятельно в тетради (отправить мне на эл. почту) – за третий пункт будет выставлена оценка!
1. Минимумом называют точку на , в которой значение функции меньше, чем в соседних точках.
2. Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.
Минимумы и максимумы вместе именуют экстремумами функции.
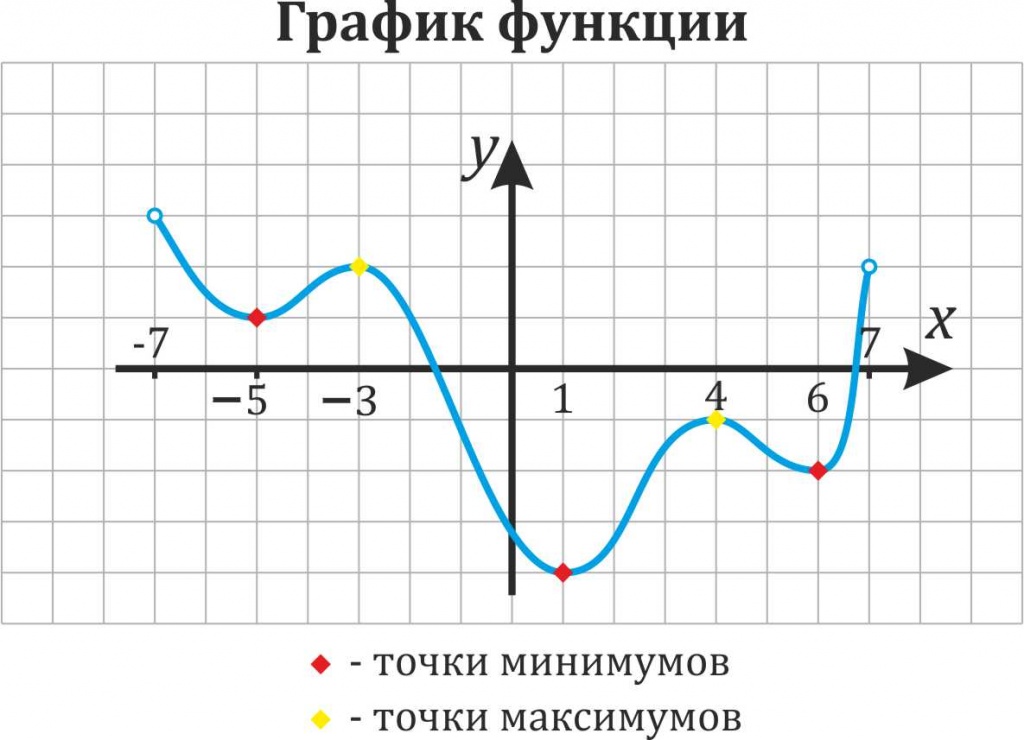
Иными словами, все пять точек, выделенных на графике ниже, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. y. Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке ниже, −5 точка минимума, а 1 – минимум (или экстремум - смотрим по ОУ).
3. Как найти точки экстремумов функции по графику производной?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки −13, −11, −9,−7 и 3. Количество точек экстремума функции 5.
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось x).
4. Как найти точки максимумов или минимумов функции по графику производной)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
- Производная положительна там, где функция возрастает. - Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди −13, −11, −9,−7 и 3.
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с−13: до −13 производная положительна т.е. функция растет, после - производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что −13 – точка максимума.
−11: производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что −11 – это минимум.
−9: функция возрастает, а потом убывает – максимум.
−7: минимум.
3: максимум.
Все вышесказанное можно обобщить следующими выводами:
- Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус. - Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции f′(x).
- Найдите корни уравнения f′(x)=0.
- Нарисуйте ось x и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью f′(x), а под осью f(x).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2: - если f′(x) изменила знак с «+» на «−», то x1 – точка максимума; - если f′(x) изменила знак с «−» на «+», то x3 – точка минимума; - если f′(x) не изменила знак, то x2 – может быть точкой перегиба.
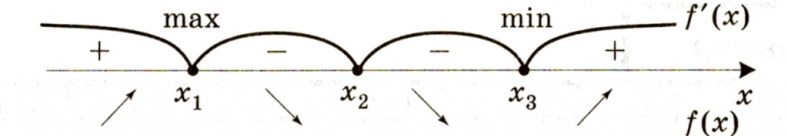
Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.
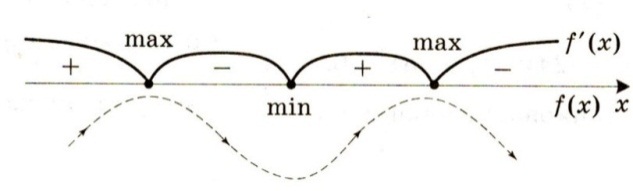
2.Рассмотрим примеры:
Пример 1.
Найдите точку максимума функции y=3x5−20x3−54. Решение:
1.Найдем производную функции: y′=15x4−60x2. 2. Приравняем её к нулю и решим уравнение:
15x4−60x2=0 |:15 x4−4x2=0 x2(x2−4)=0 x=0 x2−4=0 x=±2
3. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
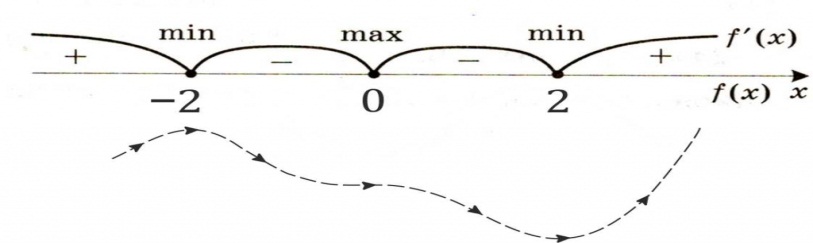
Теперь очевидно, что точкой максимума является −2.
Ответ. −2.
Пример 2.
Найдите точку максимума функции 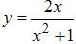
Решение 1. Найдём производную (по правилу производная дроби) и приравниваем её к нулю:
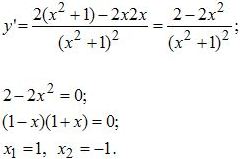 Полученные значения переменных наносим на координатную прямую и высчитываем знак производной на каждом из промежутков. Ну например, для первого возьмём -2, тогда производная будет равна -0,24, для второго возьмём 0, тогда производная будет 2, а для третьего возьмём 2, тогда производная будет -0,24. Проставляем соответствующие знаки.
Полученные значения переменных наносим на координатную прямую и высчитываем знак производной на каждом из промежутков. Ну например, для первого возьмём -2, тогда производная будет равна -0,24, для второго возьмём 0, тогда производная будет 2, а для третьего возьмём 2, тогда производная будет -0,24. Проставляем соответствующие знаки.
 Видим, что при прохождении через точку -1 производная меняет знак с минуса на плюс, то есть это будет точка минимума, а при прохождении через 1 – с плюса на минус, соответственно это точка максимума. Ответ: 1.
Видим, что при прохождении через точку -1 производная меняет знак с минуса на плюс, то есть это будет точка минимума, а при прохождении через 1 – с плюса на минус, соответственно это точка максимума. Ответ: 1.
3. Исследовать на экстремумы функцию (самостоятельно):
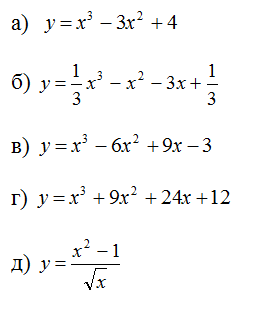
КРИТЕРИИ «5» - все 5 функций
«4» - 3,4 функции
«3» - 2 функции
Решение 3 пункта записываете в тетрадь и предоставляете для проверки, оценка выставляется в ГИС






