Тригонометрия
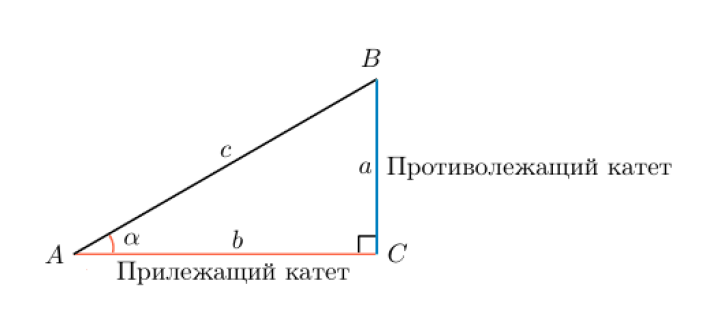 В геометрии углом называется фигура, образованная двумя лучами, выходящими из одной точки.
В геометрии углом называется фигура, образованная двумя лучами, выходящими из одной точки.
В прямоугольном треугольнике синусом угла является отношение катета, противолежащего искомому углу, к гипотенузе треугольника.
Соответственно, косинус — это отношение прилежащего катета и гипотенузы.
Оба эти значения всегда имеют величину меньше единицы, так как гипотенуза всегда длиннее катета.
Радианная мера угла
Любой угол можно рассматривать как результат вращения луча в плоскости вокруг начальной точки. Вращая луч вокруг точки О от начального положения OA до конечного положения ОВ, получим угол АОВ.
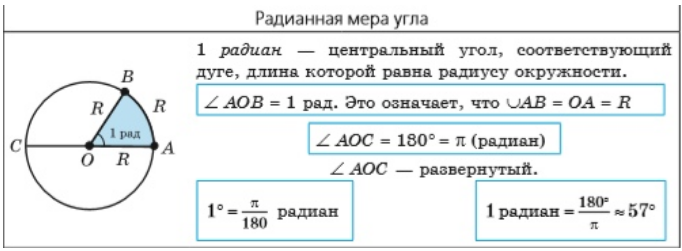
Понятие об измерении углов известно из геометрии. При измерении углов принимают некоторый определенный угол за единицу измерения и с ее помощью измеряют другие углы. За единицу измерения можно принять любой угол.
На практике уже более трех тысяч лет за единицу измерения величины угла принята 1/360 часть полного оборота, которую называют градусом.
Радианная (радиусная) мера угла появилась в трудах Ньютона (1643—1727) и Лейбница (1646—1716) и вошла в науку благодаря трудам академика Петербургской академии наук Леонарда Эйлера (1707—1783).
Если α – длина дуги единичной окружности, градусная мера которой равна β, то
α = 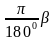 . Таким образом, дуга в 1 радиан содержит
. Таким образом, дуга в 1 радиан содержит 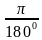 градусов:
градусов:
Дуга в 1° = 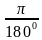 радиан
радиан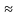
 , 1 радиан
, 1 радиан 
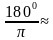 57017′
57017′
Радианная мера угла позволяет установить взаимно однозначное соответствие между множеством углов и рядом действительных чисел. Это возможно, поскольку с одной стороны - это число, равное 3,14… с другой стороны это угол, соответствующий 180о. Таким образом, нетрудно установить взаимоноднозначное соответствие между углами от 0 до 360о и действительными числами от 0 до .
Градусная мера угла
Поворот, равный полного оборота против часовой стрелки задает угол в один градус.
Различают также следующие доли градуса:
1 минута = 1' = 1/60 градуса;
1 секунда = 1'' = 1/60 минуты = 1/3600 градуса.
Угол, равный 180о или половине полного оборота называют развернутым, равный 90о или четверти полного оборота - прямым.
Угол считается положительным, если переход от его начальной стороны к конечной совершается вращением подвижного луча против часовой стрелки, и отрицательным, если такой переход совершается вращением по часовой стрелке.
Единичный круг - круг с центром в начале координат и радиусом, равным по длине единице. Окружность этого круга называется единичной окружностью.
Координатные оси делят единичный круг и его окружность на четыре равные части, которые называются четвертями, или квадрантами.
Синус - отношение ординаты конца подвижного радиуса к длине этого радиуса.
Косинус - отношение абсциссы конца подвижного радиуса к длине этого радиуса.
Тангенс - отношение ординаты конца подвижного радиуса к его абсциссе.
Котангенс - отношение абсциссы конца подвижного радиуса к его ординате.
Секанс - отношение длины подвижного радиуса к абсциссе его конца.
Косеканс - отношение длины подвижного радиуса к ординате его конца.
Тригонометрические функции числового аргумента.
Р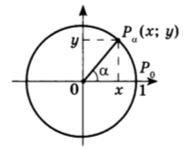 анее было установлено взаимно однозначное соответствие между множеством всех действительных чисел и множеством точек единичной окружности. Каждому действительному числу α поставлена в соответствие точка Мα единичной окружности. Пусть на плоскости выбрана прямоугольная система координат так, что ее начало совпадает с центром рассматриваемой единичной окружности, а единичная точка оси абсцисс совпадает с точкой А. Пусть хα, уα — координаты точки Мα. Тогда каждому числу α поставлены в соответствие два числа хα и уα.
анее было установлено взаимно однозначное соответствие между множеством всех действительных чисел и множеством точек единичной окружности. Каждому действительному числу α поставлена в соответствие точка Мα единичной окружности. Пусть на плоскости выбрана прямоугольная система координат так, что ее начало совпадает с центром рассматриваемой единичной окружности, а единичная точка оси абсцисс совпадает с точкой А. Пусть хα, уα — координаты точки Мα. Тогда каждому числу α поставлены в соответствие два числа хα и уα.
Число уα.называется синусом α и обозначается sin α,
а число хαназывается косинусом α и обозначается cos α.
Функция sin α, 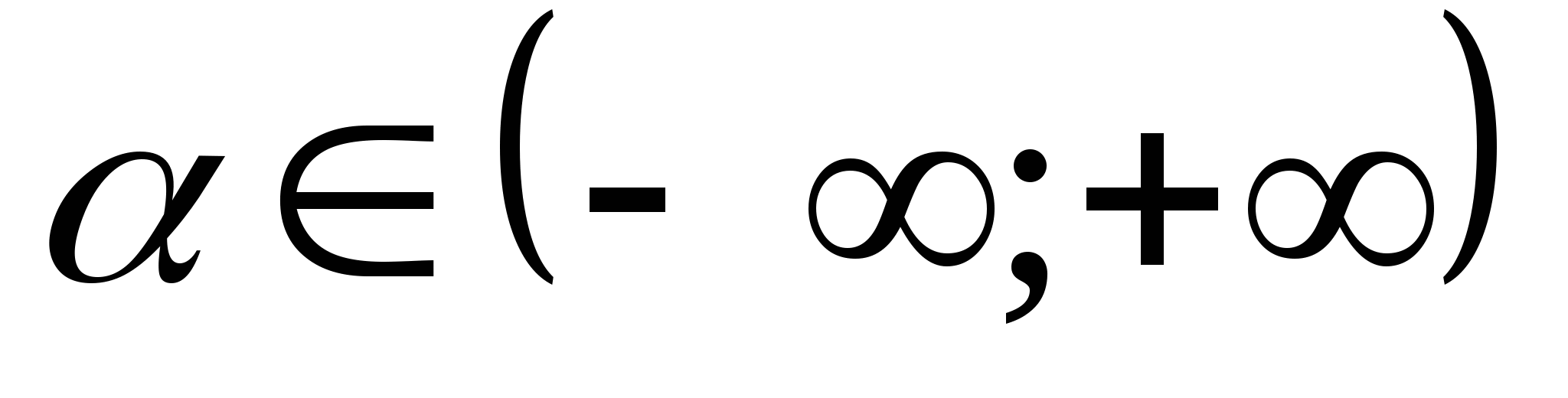 , называется синусом.
, называется синусом.
Функция cos α, 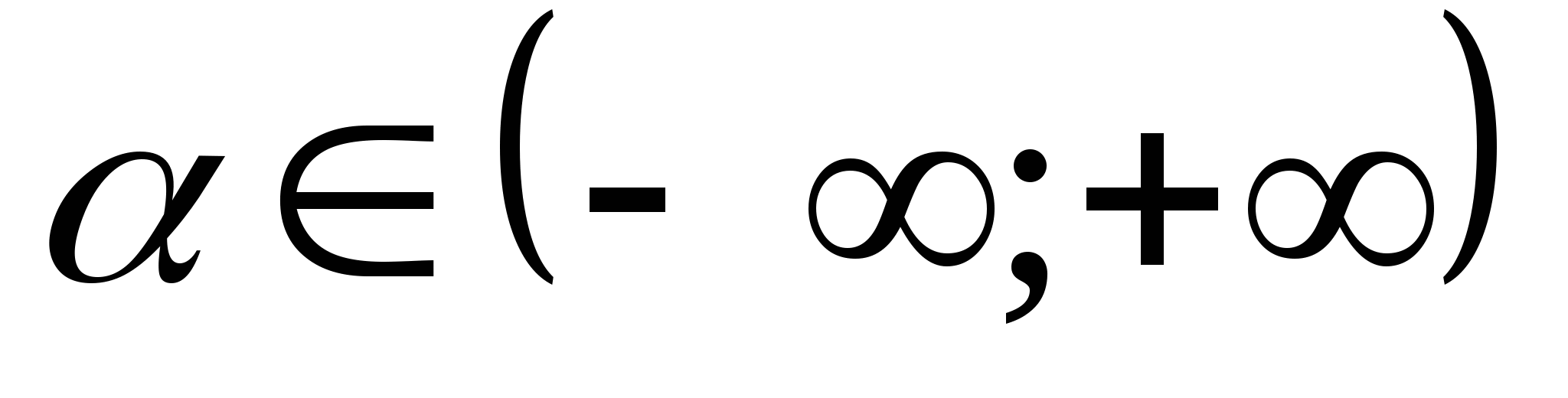 , называется косинусом.
, называется косинусом.
Периодичность тригонометрических функций.
Тригонометрические функции являются периодическими функциями
Теорема: Число 2π является минимальным периодом синуса и косинуса.
Это следует из того, что значение тригонометрических функций определяются с помощью координат вращающейся точки.
Но при вращении этой точки по единичной окружности через каждый оборот она занимает тоже самое положение, как известно полный оборот точка совершает тогда, когда приращение аргумента равно 2π. Следовательно, sin (t +2π) = sin t, аналогично, и для cos (t +2π) =cos t.
Тангенс и котангенс также являются периодическими функциями, но наименьшим периодом для тангенса и котангенса является π.
Пример 4: Найти sin 2672° = sin (7·360° + 152°)= sin 152°
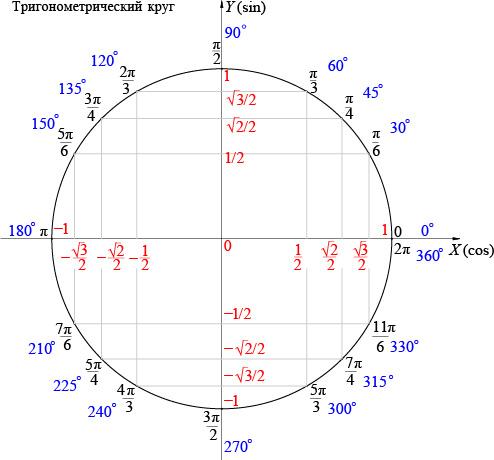
А теперь подробно о тригонометрическом круге: нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями 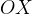 и
и 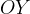 , в которой мы привыкли рисовать графики функций.
, в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси 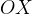 против часовой стрелки.
против часовой стрелки.
Полный круг 360 градусов. Точка с координатами 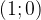 соответствует углу ноль градусов. Точка с координатами
соответствует углу ноль градусов. Точка с координатами 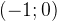 отвечает углу в
отвечает углу в 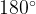 , точка с координатами
, точка с координатами 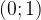 — углу в
— углу в 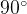 . Каждому углу от нуля до
. Каждому углу от нуля до 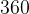 градусов соответствует точка на единичной окружности.
градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси  ) точки на единичной окружности, соответствущей данному углу
) точки на единичной окружности, соответствущей данному углу  .
.
Синусом угла называется ордината (то есть координата по оси 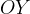 ) точки на единичной окружности, соответствущей данному углу
) точки на единичной окружности, соответствущей данному углу 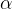 .
.
Например:
 ;
; 


Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса  , синус — ордината
, синус — ордината  . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от
. Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от  до
до  :
:
 ,
, 
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу 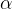 , смотрим, положительны или отрицательны ее координаты по
, смотрим, положительны или отрицательны ее координаты по  (это косинус угла
(это косинус угла 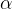 ) и по
) и по  (это синус угла
(это синус угла 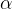 ).
).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: 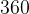 градусов, то есть полный круг, соответствует
градусов, то есть полный круг, соответствует  радиан. На нашем рисунке подписаны и градусы, и радианы.
радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол  — это угол величиной в
— это угол величиной в  , который отложили от положительного направления оси
, который отложили от положительного направления оси  по часовой стрелке.
по часовой стрелке.
Легко заметить, что  ,
,  .
.
Углы могут быть и больше 360 градусов. Например, угол 732 градуса — это два полных оборота по часовой стрелке и еще 12 градусов. Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по  и по
и по  , значения синуса и косинуса повторяются через
, значения синуса и косинуса повторяются через  . То есть:
. То есть:
 ,
,
 ,
,
где  — целое число. То же самое можно записать в радианах:
— целое число. То же самое можно записать в радианах:
 ,
,
 .
.
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
 ,
,  .
.
Пример 1: Найти синус числа .
Решение: Так как , то этому соответствует та же точка М, что и числу Опустим из точки М перпендикуляр MP на ось Ох (рис. 4), имеем |РМ| = у. В прямоугольном треугольнике РОМ длина гипотенузы ОМ равна 1 (так как окружность единичная), длина катета РМ равна (как катет, лежащий против угла в 30º). Следовательно, ордината точки М равна числу 0,5, т. е. у = 0,5.
Легко видеть, что tg α определен для всех действительных чисел .
Функция tg α, , называется тангенсом. Легко видеть, что ctg α определен для всех действительных чисел а .
Функция ctg α, , называется котангенсом.
Реже используются функции секанс и косеканс
Знаки тригонометрических функций.
Знаки тригонометрических функций определяются тем, в какой из координатных четвертей плоскости лежит рассматриваемый угол.
Так как синус числа α является ординатой конца единичного вектора с началом в начале координат, то синус положителен в первой и второй четвертях и отрицателен в третей и четвертой.
Косинусом числа α есть абсцисса конца вектора. Поэтому косинус положителен в первой и четвертой четвертях и отрицателен - во второй и третей.
Тангенс и котангенс есть отношение координат, поэтому они положительны когда координаты имеют одинаковые знаки (первая и третья ) и отрицательны, когда разные (вторая и четвертая).
Пример: Найти знак sin 2735° Ответ: 2735° = 7 · 360° + 215°. Так как 360° = 2π, а синус есть периодическая функция с периодом 2π, то знак синуса зависит только от величины угла 215°, который расположен в третьей четверти, где синус отрицателен. Следовательно, sin 2735º = sin 215º
Пример: Определить знак следующего выражения sin 300° · cos 200°. Ответ: sin 300° 0.
Четность и нечетность тригонометрических функций.
Докажем, что косинус – функция четная, а синус, тангенс и котангенс – функции нечетные. Пусть дана единичная окружность с центром в начале координат. Любые два противоположных действительных числа α и — α можно изобразить на этой окружности двумя точками Мα и М-α, симметричными относительно оси абсцисс (рис. 6). Так как точки Мα и М-α лежат на единичной окружности, то координатами точки Мαбудут числа cos α и sin α, а координатами точки М-α будут числа cos (– α) и sin (– α). Так как точки Мα и М-α, симметричны относительно Ох, то их абсциссы совпадают, а ординаты противоположны. На основании этого для любых допустимых чисел αсправедливы равенства:
Формула (1) означает, что косинус – функция четная, а формулы (2), (3), (4) означают, что синус, тангенс и котангенс – функции нечетные, что и требовалось доказать. Например :
Основные тригонометрические тождества
Итак, напомним, что при рассмотрении тригонометрических функций, мы используем единичную окружность, с радиусом, равным единице. Рассмотрим произвольный прямоугольный треугольник, полученный в результате движения радиус-вектора на некоторый угол.
К прямоугольному треугольнику применима теорема Пифагора, в соответствии с которой квадрат гипотенузы будет равен сумме квадратов остальных сторон треугольника. Так как мы знаем, что синусу соответствует значение ординаты на плоскости, то есть величина противолежащего катета, а косинусу значение абсциссы (прилежащего катета). Так же нам известно, что гипотенуза треугольника является радиусом окружности, длина которого равна единицы, то теорему Пифагора можем получить в следующем виде: sin2α + cos2α = 1
Тригонометрические тождества мы можем получить, зная определение тангенса и котангенса.
Давайте перемножим первое и второе уравнение и посмотрим, что получилось. В результате данного математического действия получим, что произведение тангенса на котангенс равно единице: tgx+ctgx =1
А теперь давайте возьмем первое основное тождество и почленно разделим все на cos2α или на sin2α. В результате этого получим:
Первое тождество справедливо для всех углов. Остальные же используются исключительно при углах, синус и косинус которых не равен 0.
Пример: Найдите значения cos α, tg α, ctg α, если sin α =  .
.
Ответ: Так как , то .
Используя соотношения
Остальные т и имеем: и






 В геометрии углом называется фигура, образованная двумя лучами, выходящими из одной точки.
В геометрии углом называется фигура, образованная двумя лучами, выходящими из одной точки.
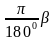 . Таким образом, дуга в 1 радиан содержит
. Таким образом, дуга в 1 радиан содержит 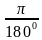 градусов:
градусов: 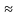
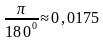 , 1 радиан
, 1 радиан 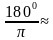 57017′
57017′ анее было установлено взаимно однозначное соответствие между множеством всех действительных чисел и множеством точек единичной окружности. Каждому действительному числу α поставлена в соответствие точка Мα единичной окружности. Пусть на плоскости выбрана прямоугольная система координат так, что ее начало совпадает с центром рассматриваемой единичной окружности, а единичная точка оси абсцисс совпадает с точкой А. Пусть хα, уα — координаты точки Мα. Тогда каждому числу α поставлены в соответствие два числа хα и уα.
анее было установлено взаимно однозначное соответствие между множеством всех действительных чисел и множеством точек единичной окружности. Каждому действительному числу α поставлена в соответствие точка Мα единичной окружности. Пусть на плоскости выбрана прямоугольная система координат так, что ее начало совпадает с центром рассматриваемой единичной окружности, а единичная точка оси абсцисс совпадает с точкой А. Пусть хα, уα — координаты точки Мα. Тогда каждому числу α поставлены в соответствие два числа хα и уα.




















