Использование ИКТ технологий на уроках математики

Муниципальное бюджетное общеобразовательное учреждение

Злынковская средняя общеобразовательная школа №2

На тему:

Подготовила учитель математики и информатики

Коваленко Алла Петровна

2014-2015 учебный год

Учи и учись лучшему!
Фалес Милетский

 Учитель и ученик… Даже человеку, далёкому от педагогики, понятно, что без взаимодействия этих составляющих невозможен образовательный процесс, а следовательно, невозможно развитие общества, которому необходимы грамотные специалисты и творческие люди. Поэтому особая роль предназначена учителю.

“Авторитет, личность педагога, его разнообразные достоинства являются залогом успеха учащихся”, – утверждал В.М. Лизинский.

Главная задача каждого преподавателя – не только дать учащимся определенную сумму знаний, но и развить у них интерес к учению, творчеству, воспитывая, таким образом, активно мыслящую личность.

Урок рассматривается сегодня не только как деятельность учителя, т.е. как форма обучения, но и как деятельность ученика, т.е. как форма учения. 

Интерес же к предмету вырабатывается, на мой взгляд, тогда, когда ученику понятно то, о чем говорит преподаватель, когда интересны по содержанию задачи и упражнения, которые побуждают школьника к творчеству, способствуют проявлению самостоятельности при овладении учебным материалом, учат не только делать выводы и обобщения, но и видеть перспективу применения полученных знаний на уроке, развивают их индивидуальные особенности. Вот почему учитель должен стремиться к обновлению системы преподавания, направленному на повышение мотивации школьников к учебному процессу.

Использование компьютерных технологий изменяет цели и содержание обучения: появляются новые методы и организационные формы обучения.

Мы рассмотрим следующие варианты использования средств ИКТ в образовательном процессе:

• урок с мультимедийной поддержкой – в классе стоит один компьютер, им пользуется не только учитель в качестве “электронной доски” (демонстрация рисунков, опытов, виртуальные экскурсии), но и ученики для защиты проектов;

• урок проходит с компьютерной поддержкой – несколько компьютеров (обычно, в компьютерном классе), за ними работают все ученики одновременно или по очереди выполняют лабораторные работы, тесты, тренировочные упражнения;

• урок, интегрированный с информатикой, проходит в компьютерном классе и преследует следующие задачи: во-первых, отработать учебный материал, используя ПК для создания кроссвордов, графиков, игр, таблиц и схем; во-вторых, изучить возможности различных компьютерных программ;

• работа с электронным учебником (возможно дистанционное) с помощью специальных обучающих систем, где традиционные уроки по предмету заменяются самостоятельной работой учащихся с электронными информационными ресурсами.

Для успешного проведения урока с применением компьютерных технологий учителю приходится решать следующие задачи:

дидактическую (подготовка учебного материала урока, конкретная компьютерная программа);

методическую (определить методы использования компьютера в преподавании темы, анализ результатов урока, постановка следующей учебной цели);

организационную(организовать работу, избегая перегрузки учащихся и нерациональной траты времени); учебную (выработать и закрепить у учащихся знания по рассматриваемой теме, умения и навыки работы с предложенной программой). 

Приведу в качестве примеров виды деятельности с использованием компьютера на различных этапах обучения. 
1. Этап актуализации субъектного опыта учащихся. . На этапе актуализации опыта учащихся возможно и желательно использовать компьютерные презентации содержащие игры, графические диктанты.

Приложение 1. Умножение многочлена на многочлен 1.

2. На этапе усвоения новых знаний возможно и желательно использовать компьютерные презентации как наглядное пособие и источник учебной информации. Визуальное представление определений, формул, теорем и их доказательств, качественных чертежей к геометрическим задачам, предъявление подвижных зрительных образов в качестве основы для осознанного овладения научными фактами обеспечивает эффективное усвоение учащимися новых знаний и умений. 

Приложение 1. Решение задач с помощью уравнений.

Приложение 2. Основное свойство дроби.

Приложение 3. ЛИНЕЙНАЯ ФУНКЦИЯ y=kx.

Приложение 4. Презентация к уроку - Электронные таблицы 9 класс

3. Этап проверки понимания и закрепления учащимися новых знаний и способов действий включает в себя: тесты, дидактические игры, диктанты. Все это также может быть представлено в виде презентаций. В реализации это один из самых простых этапов. И, что немаловажно, можно наблюдать почти сразу положительный педагогический эффект: быстрое получение результатов, отсутствие субъективного фактора. 

Приложение 1. Умножение многочлена на многочлен 2.

Приложение 2. Свойства степени с натуральным показателем 1.

Приложение 3. Свойства степени с натуральным показателем 2.

3.Проектная деятельность учащихся. Общество становится все более зависимым от информационных технологий, поэтому учащиеся могут применять возможности компьютера в исследовательской деятельности, использовать многогранные возможности Internet в образовательных целях. 

Применяя же ИКТ-технологии, учитель не только даёт знания, но еще и показывает их границы, обучает школьников приёмам обработки информации, разным видам деятельности; сталкивает ученика с проблемами, решения которых лежат за пределами изучаемого курса, что нацеливает их на поиски нестандартных решений, на самообразование; благодаря такой работе ученик сможет максимально раскрыться, показать все свои возможности и способности, проявить и развить свои таланты. А главное – найти себя, почувствовать свою значимость и осознать, что он – личность, способная мыслить, творить, создавать новое. И, следовательно, учитель выполнил своё предназначение: “нести огонь идеального!”

Использование

ИКТ-технологий

на

уроках математики

Виды уроков

урок с мультимедийной поддержкой;

урок проходит с компьютерной;

урок, интегрированный с информатикой;

работа с электронным учебником.

Умножение

многочлена

на

многочлен

Верно ли утверждение, определение, свойство?

• Одночленом называют сумму числовых и буквенных множителей. 

2. Буквенный множитель одночлена, записанного в стандартном виде,

называют коэффициентом одночлена.

3. Целое выражение, которое содержит произведение чисел и букв,

называют одночленом.

4. Сумма показателей степеней всех букв входящих в одночлен называют

степенью одночлена.

5. Одинаковые или отличающиеся друг от друга только коэффициентами

одночлены, называют подобными членами.

6. Алгебраическая сумма нескольких одночленов называется одночленом.

7. В результате умножения многочлена на одночлен получается одночлен.

8. В результате умножения одночлена на многочлен получается многочлен.

9. Многочлен в котором отсутствуют подобные члены и каждый из них

одночлен стандартного вида называется многочленом стандартного

вида.

10. Чтобы раскрыть скобки, перед которыми стоит знак "+”,

скобки надо опустить, сохранив знак каждого члена, который был

заключен в скобки.

  11. Когда раскрываем скобки, перед которыми стоит знак "-”, скобки

опускаем, и знаки членов, которые были заключены в скобки, меняют

на противоположные 

Проверка

--^^^--^^^^

Шкала оценок

«5»- ошибок нет;

«4» - две ошибки;

«3» - четыре ошибки;

«2» - больше четырех ошибок.

Решение задач

с помощью уравнений

мука

4x+1+2

5+5+5

=

x

x

x

x

мука

мука

мука

5кг

5кг

5кг

2кг

1кг

24

+9

-12

7

Было x пас.

I ост. cтало (x+9)

II ост. стало (x+9)-12

x

-12

=24

+9

7

5кг

Для детского сада купили 23 кг яблок. Несколько килограммов съели на полдник, ещё 5кг – на ужин. После этого осталось 7кг? Сколько килограммов яблок съели на полдник?

23кг

7кг

x

=7

23–x

5кг

– 5

Было 23 кг

Взяли x кг

Осталось 23-x

Взяли 5 кг

Осталось 23-x-5 = 7

23кг

7кг

на машине Весь путь 46 км на 7км на лодке пешком" width="640"

на14км

на машине

Весь путь 46 км

на 7км

на лодке

пешком

на машине x+7+14 Весь путь 46 км на 7км x x+7 на лодке пешком Пешком х км На лодке х + 7 На машине х + 7 + 14 46 км" width="640"

на14км

на машине

x+7+14

Весь путь 46 км

на 7км

x

x+7

на лодке

пешком

Пешком х км

На лодке х + 7

На машине х + 7 + 14

46 км

Основное

свойство

дроби

По рисунку объясните, почему равны дроби:

4

4

4

4

Если числитель и знаменатель дроби

умножить

на одно и то же натуральное число, то получится равная ей дробь.

Математика 6 класс. Н.Я.Виленкин. № 202.

или разделить

15

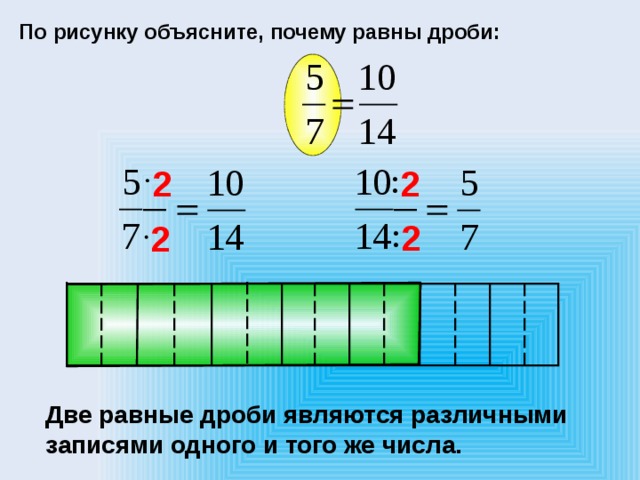
По рисунку объясните, почему равны дроби:

2

2

2

2

Математика 6 класс. Н.Я.Виленкин. №202

Две равные дроби являются различными записями одного и того же числа.

16

ЛИНЕЙНАЯ ФУНКЦИЯ y=kx И ЕЕ ГРАФИК.

На координатной плоскости построены графики линейных функций:

y=x,

y=0,5x;

y=-x;

y=-4x

y =-x

y=-4x

y

0

x

y=x

y=0,5x

1

1

-1

-1

Определите, что общего в данных графиках?

Чем отличаются графики данных линейных функций?

y =-x

y=-4x

y

0

x

y=x

y=0,5x

1

1

-1

-1

Все графики данных линейных функций проходят через начало координат (0;0)

y = - x

y= -4 x

y

0

x

1

1

-1

-1

Если коэффициент k , то линейная функция убывает и находится во второй и четвертой четвертях.

0 , то линейная функция возрастает и находится в первой и третьей четвертях." width="640"

y

0

x

y=x

y= 0,5 x

1

1

-1

-1

Если коэффициент k0 , то линейная функция возрастает и находится в первой и третьей четвертях.

Постройте график линейной функции: а) y=2x, б) y=-3x. На одной координатной плоскости. Что вы можете сказать про графики данных линейных функций?

Решение.

• Находим координаты точек для линейной функции y=2x:

y=2 · 0 = 0 ; О( 0 ; 0 )

y=2· 3 = 6 ; А( 3 ; 6 ).

Переносим точки на координатную плоскость.

• Строим график данной линейной функции и, обязательно , его подписываем.

X

0

y

3

0

6

y

А

0

x

y=2x

6

1

1

3

-1

-1

Решение.

• Находим координаты точек для линейной функции y=-3x:

y=-3 · 0 = 0 ; О( 0 ; 0 )

y=-3· (-3) = 9 ; В( -3 ; 9 ).

• Переносим точки на координатную плоскость. Строим график данной линейной функции и, обязательно , его подписываем.

X

0

y

-3

0

9

y

А

0

x

В

y=2x

9

6

1

1

-3

3

-1

-1

y=-3x

0; г) решение неравенства: -2≤x≤0" width="640"

Постройте график линейной функции y=0,4x.

Найдите по графику:

а) значение y, соответствующее значению x, равному 0;5;10;-5;

б) значение x, соответствующее значению y, равному 0;2;4;-2;

в) решение неравенства: 0,4x0;

г) решение неравенства: -2≤x≤0

Вопросы:

• Что вы можете сказать про график данной линейной функции: y=0,4x?
• Какую абсциссу лучше взять, чтобы координаты точек были целыми числами?
• Для чего, координаты точек должны являться целыми числами?
• Что значит: 0,4x0?

Решение:

1. Находим координаты точек для линейной функции y=0,4x:

y=0,4 · 0 = 0 ; О( 0 ; 0 )

y=0,4· 5 = 2 ; А( 5 ; 2 ).

• Переносим точки на координатную плоскость. Строим график данной линейной функции и, обязательно , его подписываем.

x

0

y

5

0

2

y

0

x

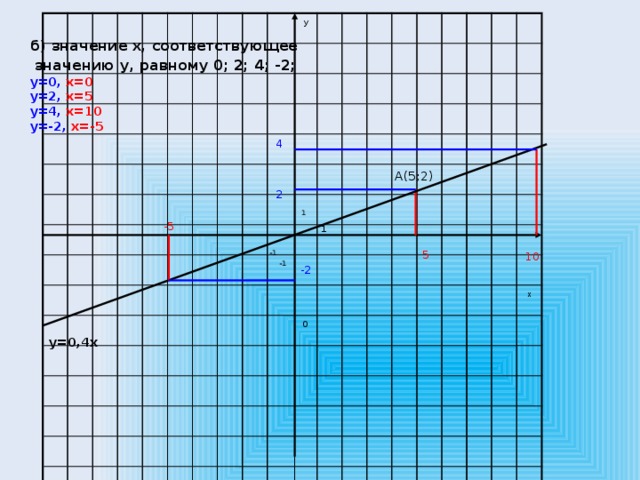
а) значение y, соответствующее

значению x, равному 0; 5; 10; -5:

x=0 , y=0

x=5 , y=2

x=10 , y=4

x=-5 , y=-2

y=0,4x

4

А(5;2)

2

1

-5

1

-10

5

-1

10

-1

-2

-4

y

0

x

б) значение x, соответствующее

значению y, равному 0; 2; 4; -2;

y=0, x=0

y=2, x=5

y=4, x=10

y=-2, x=-5

4

А(5;2)

2

1

-5

1

5

-1

10

-1

-2

y=0,4x

0. При каких значениях абсциссы x график данной линейной функции лежит выше оси ox ? Ответ: при x0. 1 1 -1 -1 y=0,4x" width="640"

y

0

x

в) решение неравенства: 0,4x0.

При каких значениях абсциссы x

график данной линейной функции лежит выше оси ox ?

Ответ: при x0.

1

1

-1

-1

y=0,4x

y

x

г) при каких значениях x,

график данной линейной функции

удовлетворяет неравенству: -2≤y≤0?

Ответ: при -5 ≤x ≤ 0.

4

А(5;2)

2

1

-5

0

1

-1

-1

-2

y=0,4x

Электронные таблицы

Программы создания ЭТ:

Microsoft Excel

OpenOffice.orgCalc

Для запуска программы

Microsoft Office Excel

Пуск 

Все программы 

Microsoft Office 

Microsoft Office Excel

Вид окна MS Excel

Кнопка «Office»

Кнопки управления окном

Строка Заголовка

Заголовок

Строка Меню

Панели инструментов

Строка состояния

Рабочая область

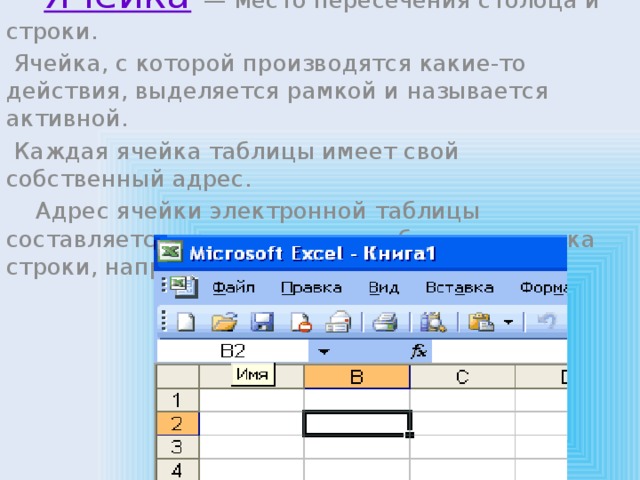
Ячейка — место пересечения столбца и строки.

Ячейка, с которой производятся какие-то действия, выделяется рамкой и называется активной.

Каждая ячейка таблицы имеет свой собственный адрес.

Адрес ячейки электронной таблицы составляется из заголовка столбца и заголовка строки, например: Al, B5, E7

Элементы ЭТ:

Столбец

Строка

Ячейка Е6

Активная ячейка С2

С2 и Е6 – адрес ячеек

Элементы ЭТ:

Книги

Рабочие

листы

Книги и Рабочие листы можно переименовывать

Основные операции над элементами ЭТ

Основные операции с элементами ЭТ

это удаление и вставка.

Эти команды находятся в меню Ячейки , которые

позволяют: Вставить ячейки, строку, столбец, лист ;

Удалить ячейки, строку, столбец, лист;

Основными информационными объектами, обрабатываемыми электронной таблицей, являются следующие типы данных:

Формула

Текст

Число

символы

Звук и рисунок в ячейку ввести нельзя

С числами в электронной таблице можно осуществлять различные математические действия (сложение, умножение, вычитание, деление, вычисление среднего арифметического, вычисление максимального/минимального значения и др.).

Текст – это совокупность символов, используемая для оформления таблицы (заголовки, пояснения и т.д.).

Формулой является выражение, задающее указание для математических вычислений.

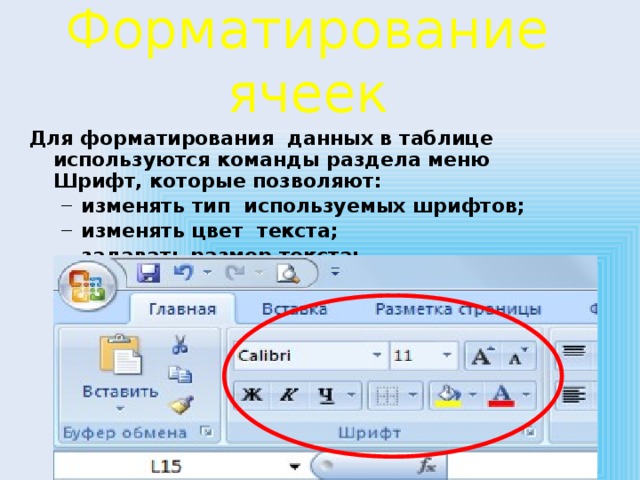
Форматирование ячеек

Для форматирования данных в таблице используются команды раздела меню Шрифт, которые позволяют:

• изменять тип используемых шрифтов; изменять цвет текста; задавать размер текста; заливать ячейки цветом.
• изменять тип используемых шрифтов;
• изменять цвет текста;
• задавать размер текста;
• заливать ячейки цветом.

Отличие ЭТ от таблиц на бумаге:

Изменилась цена,

поэтому изменились Стоимость и ИТОГО ( АВТОМАТИЧЕСКИ )

ВЫВОД : ЭТ может постоянно меняться.

Применение Э Т:

Математика:

Для построения графика функции сначала строится таблица значений.

x

y=x 3

-4

-64

y=2*x

-3

-2

-8

-27

-1

-8

-6

-4

-1

0

0

-2

1

1

2

0

2

8

3

27

4

4

64

6

8

География:

По статистическим данным строится диаграмма.

Физика:

Результаты лабораторной работы.

Умножение многочлена

на многочлен

Математический диктант

Проверьте соседа:

1 вариант

2 вариант

1 .

1 .

- х 2 +2х+8

2a 2 +8a+8

(х+2)(4-х)

(a+2)(2a+4)

2 .

Y 2 +2y-8

У 3 +5у-5у 2 -25

2 .

(у-5)(у 2 +5)

(у+4)(у-2)

3 .

3 .

(2а+8)(а 3 -2)

6 х 2 +17x-45

2а 4 -4а+8а 3 -16

(3x-5)(2x+9)

4 .

t 2 +2t-15

4в 2 -14в+12

4 .

(-4в+6)(2-в)

(t-3)(t+5)

5 .

25в 2- 4

5 .

(5в-2)(5в+2)

-c 2 -4c-3

(-c-3)(c+1)

6.

У 2 +3у-10

6.

(a-1)(a-2)

a 2- 3a+10

(у-2)(5+у)

4у 2 -у 3 -8у+32

7.

-x 2- 3x-2

7.

(у 2 +8)(4-у)

-(x+1)(x+2)

Тема урока: Свойства степени с натуральным показателем

ПРОВЕРКА ТЕОРЕТИЧЕСКОЙ ЧАСТИ

Если показатель четное число, то значение степени всегда ______________________________

Если показатель нечетное число, то значение степени совпадает

со знаком _____________________

Произведение степеней a n ·a k =a n+k При умножении степеней с ________________________ надо основание _____________________________, а показатели степеней ___________________________.

Частное степеней a n : a k =a n - k При делении степеней с ________________________ надо основание ______________________________, а из показателя делимого ____________________________.

Возведение степени в степень (a n ) к = a nk При возведении степени в степень надо основание _______________________________, а показатели степеней ___________________________.

Если показатель четное число, то значение степени всегда положительное.

Если показатель нечетное число, то значение степени совпадает

со знаком основания степени.

Произведение степеней a n ·a k =a n+k При умножении степеней с одинаковыми основаниями надо основание оставить тем же , а показатели степеней сложить.

Частное степеней a n : a k =a n - k При делении степеней с одинаковыми показателями надо основание оставить тем же, а из показателя делимого вычесть показатель делителя.

Возведение степени в степень (a n ) к = a nk При возведении степени в степень надо основание оставить прежним , а показатели степеней перемножить .

Тема урока: Свойства степени с натуральным показателем

А О В С Т Л К Р И Ч Г Н М О

1. С 4 ∙С 3 5. (С 2 ) 3 ∙ С 5

2. (С 5 ) 3 6. С 6 ∙ С 5 : С 10

3. С 11 : С 6   7. (С 4 ) 3 ∙С 2

4. С 5 ∙С 5 : С

______________________________________

Шифр: А- С 7 В- С 15 Г - С И - С 30

К - С 9 М – С 14 Н - С 13 О- С 12 Р- С 11

С- С 5 Т- С 8 Ч- С 3

ОТВЕТ: ОТЛИЧНО!