53
I.8. КОДИРОВАНИЕ ИНФОРМАЦИИ
ПОНЯТЬ
Информационный процесс кодирования информации встречается в нашей жизни на каждом шагу. Любое общение между людьми происходит именно благодаря тому, что они научились выражать свои образы, чувства и эмоции с помощью специально предназначенных для этого знаков - звуков, жестов, букв и пр.
Одну и ту же информацию мы можем выразить разными способами.
ПРИМЕР
Каким образом можно сообщить об опасности?
1. Если на Вас напали, вы можете просто крикнуть “Караул!!!” (англичанин крикнет “Help me!”);
2. Если прибор под высоким напряжением, то требуется оставить предупреждающий знак (рисунок “черепа” или молнии);
3. На оживленном перекрестке регулировщик помогает избежать аварии с помощью жестов;
4. В театре пантомимы вся информация передается зрителю исключительно с помощью мимики и жестов;
5. Если Ваш корабль тонет, то Вы передадите сигнал “SOS” (...---...), для этих целей на флоте могут использовать также семафорную и флажковую сигнализацию.
В каждом из этих примеров необходимо знать правило, по которому отображается информация. Такое правило назовем кодом.
Чаще всего кодирование - это процесс представления информации в виде дискретных знаков, поскольку дискретные сигналы воспринимать и обрабатывать проще, чем непрерывные.
Знак - это элемент конечного множества, отличных друг от друга элементов.
Знак вместе с его смыслом называют символом.
Набор знаков, в котором определен порядок знаков, называется алфавитом.
Существует множество алфавитов.
- алфавит кириллических букв { А, Б, В, Г, Д, Е, ...}
- алфавит латинских букв {A, B,C,D,E,F,...}
- алфавит десятичных цифр{0,1,2,3,4,5,6,7,8,9}
- алфавит знаков зодиака {,,,,,,,,,,, } и другие.
Существуют, однако, наборы знаков, для которых нет какого-то общепринятого порядка:
- набор знаков азбуки Брайля (для слепых);
- набор китайских идеограмм;
- математическая символика (, , , , и др.);
- набор знаков генетического кода (А, Ц, Г, Т).
Важнейшие технические коды для кодирования текстов на естественных языках возникли с появлением электрического телеграфа, например,
- азбука Морзе;
- набор знаков второго международного телеграфного кода (телекс).
При кодировании информации для технических устройств особенно важное значение имеют наборы, состоящие всего из двух знаков, которые могут обозначаться: {+, -}; {. , -}; {0, 1}; {да, нет}.
Алфавиты, состоящий из двух знаков называют двоичными, а каждый знак из этого алфавита называется двоичным знаком
Кодирование используется для представления информации в виде, удобном для хранения и передачи. Рассмотрим простейшие задачи кодирования и декодирования.
ПРИМЕР
Попробуем закодировать числа от нуля до ста, не используя арабских или римских цифр.
Прежде всего необходимо придумать алфавит или выбрать какой-либо из известных.
Можно ли использовать в качестве “букв” алфавита { *, +, !, #, & }?
А знаки {, , }?
А гласные буквы русского алфавита?
Да, можно выбрать любой набор отличающихся друг от друга знаков.
Каждому числу, которое нужно закодировать, поставим в соответствие одну “букву” выбранного нами алфавита. Например:
| Числа | 1 алф | 2 алф | 3 алф |
| 0 1 2 3 4 5 6 7 8 9 10 11 | * + ! # & | | а е ё и о у ы э ю я |
Во всех трех случаях мы не решили поставленной задачи. Мы не смогли закодировать числа от одного до ста, используя предложенные алфавиты. Получается, что наш алфавит “должен” состоять из ста одного знака? Но с помощью всего десяти арабских цифр Вы можете записать любое число. А римских цифр для кодирования первых ста одного числа требуется всего пять: I,V, X, L, C.
Нужен другой подход, другое правило.
Покажем, что используя всего три символа, например {, , }, можно закодировать (зашифровать, представить) любое число. Для этого каждое число будем представлять не одним, а несколькими символами из нашего алфавита.
В нашем правиле появляется понятие “длина кода”.
Длиной кода назовем то количество знаков, которое используется для представления кодируемого числа (или слова).
ЗАМЕЧАНИЕ
Количество символов в алфавите кодирования и длина кода - совершенно разные вещи. Например, в русском алфавите 33 буквы, а слова могут быть длиной в 1, 2, 3, ... буквы.
Посмотрим, сколько чисел мы можем закодировать, если длина кода не больше двух символов.
Воспользуемся правилом, схематично представленном на рис. ..
| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 | |
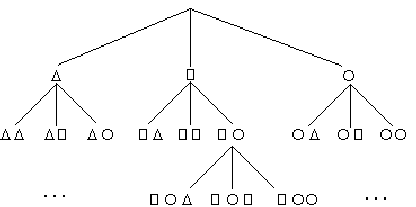
Если посмотреть на схему, то видно, что на первое место в каждом коде ставится код вершины предыдущего уровня, а к нему дописывается по очереди каждый знак алфавита. Такое правило кодирования позволяет “перебрать” все возможные коды и никогда не повториться.
Из примера видно, что при длине кода не более двух знаков всего можно закодировать 12 (3+9) разных “состояний”-чисел. Чтобы закодировать числа 12,13, ... следует увеличивать длину кода.
ПРИМЕР
Обратная задача. Есть закодированное число: .
Коды Вам известны. Определите исходное число.
Так как по нашему правилу длина кода может быть 1 или 2, то
могли быть закодированы три числа 1, 2, 0
могли быть закодированы два числа 1, 9
могли быть закодированы два числа 8, 0.
Все три решения справедливы. Как Вы думаете, почему? Есть ли способ, который приведет нас к однозначному решению поставленной задачи?
Коды непостоянной длины в технике встречается довольно редко. Исключением является лишь код Морзе.
ПРИМЕР
Взгляните на международную азбуку Морзе.
| A B C D E F G H I | . - - . . . - . - . - . . . . . - . - - . . . . . . . | J K L M N O P Q R | . - - - - . - . - . . - - - . - - - . - - . - - . - . - . | S T U V W X Y Z | . . . - . . - . . . - . - - - . . - - . - - - - . . |
Для отправителя приведенная таблица выглядит вполне логично, ибо буквы в ней расположены в алфавитном порядке. Но для человека, получающего сообщения, она мало пригодна.
В каком же порядке следует расположить символы так, чтобы получив сигнал, мы могли не теряя времени, определить, какой букве соответствует данный сигнал.
Представим азбуку Морзе в виде дерева.
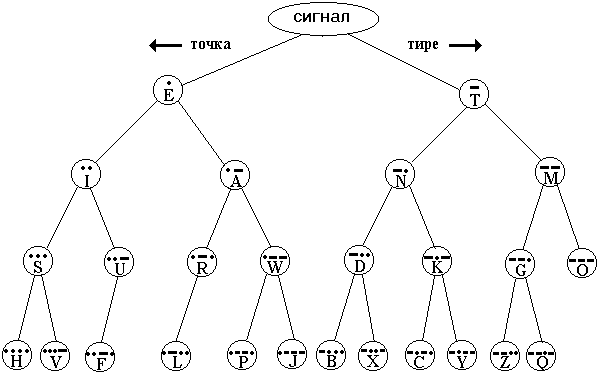
При получении сигнала - это либо точка, либо тире - формально “спускаемся” по дереву: если точка - влево от текущей вершины, если тире - вправо, если пауза - записываем букву текущей вершины, если длинная пауза - отмечаем конец слова.
По общепринятому правилу радистов, продолжительность точки равна продолжительности паузы, продолжительность тире равна продолжительности трех точек, продолжительность пропуска (между буквами) равна трем продолжительностям паузы.
Азбука Морзе - это пример троичного кода с набором знаков точка, тире, пауза. Необходимо использовать паузу в качестве разделителя между буквами и словами, так как длина кода непостоянна.
В кодах с постоянной длиной закодированные символы могут следовать друг за другом непосредственно, без всяких разделителей. Расположение этих символов устанавливается с помощью отсчета. И таким образом сообщение может быть раскодировано однозначно.
Применение кодов с постоянной длиной позволяет нам использовать для кодирования двоичный алфавит, как наиболее простой. Чем меньше букв в алфавите, тем проще должна быть устроена “машина” для распознавания (дешифровки) информационного сообщения. Однако, чем меньше букв в алфавите, тем большим их количеством (большей длиной кода) может быть записана одна и та же информация.
Вернемся к нашей задаче. Будем использовать для представления (кодирования) чисел от нуля до ста алфавит {, , } и код постоянной длины. Какова должна быть длина кода?
В случае, когда длина кода равняется n, алфавитом, состоящим из трех символов, можно закодировать 3n различных состояний (чисел, букв, комбинаций); двоичным алфавитом можно закодировать 2n различных состояний; алфавитом, состоящим из k знаков, можно закодировать kn различных состояний.
ИТАК, если алфавит состоит из k знаков и используется код с постоянной длиной n, то можно закодировать M = kn различных состояний.
Обратная задача: какой длины должен быть код, чтобы, используя разные алфавиты, закодировать 10, 33, 100, 200, 1000 различных символов. Проанализируйте таблицу.
| Кол-во символов в |
Длина кода | Максимум, сколько можно |
Минимальная длина кода для кодирования |
Решение задачи |
| алфавите |
| закодировать | 200 разных символов | кол. символов | длина кода |
| 2 | 1 2 3 ... n | 21 = 2 22 = 4 23 = 8 ... 2n |
27 = 128 - мало 28 = 256 - достаточно
ответ : 8 | 10 33 100 200 1000 | 4 6 7 8 10 |
| 3 | 1 2 3 4 ... n |
|
34 = 81 - мало 35 = 243 - достаточно
ответ : 5
| 10 33 100 200 1000 | 3 4 5 5 7
|
| 4 | 1 2 3 4 ... n |
|
43 = 64 - мало 44 = 256 - достаточно
ответ : 4 | 10 33 100 200 1000 | 2 3 4 4 5 |
| k | 1 2 3 ... n |
kn | Пусть k = 60
60 2 = 3600 - достаточно
ответ : 2 | 10 33 100 200 1000 | 1 1 2 2 2 |
ИТАК, чтобы закодировать M различных символов с помощью алфавита из k знаков с кодом постоянной длины, длина этого кода должна равняться (с учетом ого, что длина кода - это целое число)
n = [ logk M +1]
В вычислительной технике для кодирования информации используется двоичный алфавит {0,1}, а двоичный знак (англ. binary digit) называется бит.
Такой способ кодирования позволяет создавать достаточно простые устройства для представления и автоматического распознавания (дешифровки) программ и данных. Он позволяет максимально упростить конструкцию декодирующего устройства, ведь дешифратор должен уметь различать всего два состояния (например, 1 - есть ток в цепи, 0 - тока в цепи нет). По этой причине двоичная система и нашла такое широкое применение.
Передача сообщений всегда осуществляется во времени. Процесс кодирования также требует определенного количества времени, которым зачастую нельзя пренебрегать. При кодировании могут ставиться определенные цели и применяться различные методы. Наиболее распространенные цели кодирования:
- экономность (уменьшение избыточности сообщения, повышение скорости передачи или обработки);
- надежность (защита от случайных искажений);
- сохранность (защита от нежелательного доступа к информации);
- удобство физической реализации (двоичное кодирование информации в ЭВМ);
- удобство восприятия (схемы, таблицы).
Задачи, связанные с кодированием и декодированием сообщений, изучаются в теории кодирования - одном из разделов теории информации.
ЗНАТЬ
Знак - это элемент конечного множества, отличных друг от друга элементов.
Знак вместе с его смыслом называют символом.
Набор знаков, в котором определен порядок знаков, называется алфавитом.
Алфавит, состоящий из двух знаков, называется двоичным алфавитом.
Код (фр. code - кодекс, свод законов). Начиная с середины XIX века это слово, помимо основного значения, означало книгу, в которой словам естественного языка сопоставлены группы цифр или букв.
Кодом называется правило для преобразования одного набора знаков в другой набор знаков.
Кодированием называется процесс преобразования одного набора знаков в другой набор знаков.
Кодирование - способ хранения и передачи информации, форма представления ее на носителе.
Шифрование - это тоже кодирование сообщения отправителем, но такое, чтобы сообщение было непонятно несанкционированному пользователю.
Длиной кода назовем то количество знаков, которое используется при кодировании.
Код может быть постоянной и переменной длины.
Если длина кода равняется n, то алфавитом, состоящим из k знаков, можно закодировать М = kn различных состояний.
Чтобы закодировать М различных состояний с постоянной длиной кода, используя алфавит из k знаков, длина кода должна быть не менее n = [ logk M +1]
В вычислительной технике в настоящее время широко используется двоичное кодирование с алфавитом {0,1}. Наиболее распространенными кодами являются ASCII (American standart code for information interchange - американский стандартный код для обмена информацией), КОИ - 8 (код обмена информации длиной 8 бит), Win1251.
Одно и то же сообщение можно закодировать разными способами, то есть выразить на разном языках. В процессе развития человеческого общества люди выработали большое число языков кодирования. К ним относятся:
разговорные языки (русский, английский, хинди и др. всего более 2000);
язык мимики и жестов;
язык рисунков и чертежей;
языки науки (математические, химические, биологические и т.д. символы);
язык искусства (музыки, живописи, скульптуры);
специальные языки (эсперанто, морской семафор, азбука Морзе, азбука Брайля для слепых и т.д.)
В специальных языках особо выделим языки программирования.
Программирование - кодирование информации на языке, “понятном” компьютеру.
УМЕТЬ
ЗАДАНИЕ 1
Закодируйте сообщение “PASCAL 6.0” используя КОИ - 8
| 00100000 00100001 00100010 00100011 00100100 00100101 00100110 00100111 00101000 00101001 00101010 00101011 00101100 00101101 00101110 00101111 | пробел ! “ # $ % & ‘ ( ) * + , - . / | 00110000 00110001 00110010 00110011 00110100 00110101 00110110 00110111 00111000 00111001 00111010 00111011 00111100 00111101 00111110 00111111 | 0 1 2 3 4 5 6 7 8 9 : ; = ? | 01000000 01000001 01000010 01000011 01000100 01000101 01000110 01000111 01001000 01001001 01001010 01001011 01001100 01001101 01001110 01001111 | @ A B
C
D
E
F
G
H
I
J
K
L
M
N
O | 01010000 01010001 01010010 01010011 01010100 01010101 01010110 01010111 01011000 01011001 01011010 01011011 01011100 01011101 01011110 .... | P
Q
R
S
T
U
V
W
X
Y
Z
[ \ ]
|
ОТВЕТ: 01010000010000010101001101000011010000010100110000100000001101100010111000110000
ЗАДАНИЕ 2
Раскодируйте сообщение, переданное с помощью азбуки Морзе:
.. .-.. --- ...- . -.-- --- ..-
ЗАДАНИЕ 3
Сколько различных символов можно закодировать кодом длины 8 в алфавите
а) { 0, 1}
б) { #, $, %}
в) {A, Ц, Г, Т}
ЗАДАНИЕ 4.
Нужно закодировать в двоичном алфавите все символы, представленные на клавиатуре компьютера:
латинские буквы (26 строчных + 26 прописных);
русские буквы (33 строчных + 33 прописных);
цифры (10);
знаки препинания ( . , : ! ? - ; “ пробел);
скобки ( ( ) [ ] { } );
специальные символы (@ # $ % ^ & * );
псевдографические символы для создания таблиц
и некоторые другие.
Какая минимальная длина кода должна быть выбрана?
ЗАДАНИЕ 5
Закодируйте на различных известных вам языках кодирования информации теорему Пифагора о связи длины гипотенузы с длинами катетов.
ВОПРОС-ПРОБЛЕМА
Почему не используется кодирование в двоичном алфавите с кодом переменной длины?
ИНТЕРЕСНЫЙ ФАКТ
В 1977 году математики Р.Ривест, А.Шамил и Л.Эделман зашифровали фразу из нескольких слов, используя комбинацию из 129 цифр. Они утверждали, что на разгадку понадобятся триллионы лет. Однако ключ к самому сложному в мире шифру “РСА - 129” был найден за 17 лет. Над дешифрованием работали 600 ученых и добровольцев на пяти континентах при помощи 1600 компьютеров. Сложность шифра заключалась в том, что для его разгадки было необходимо определить две группы простых чисел, которые при умножении давали код “РСА - 129”. Зашифрованной оказалась бессмысленная фраза “волшебные слова -щепетильная скопа” (скопа - это хищная птица, живущая у водоемов и питающаяся рыбой). Эти слова были наугад выбраны из словаря в 1977 году. “Такие шифры необходимы, если Вы хотите сохранить в секрете рецепт приготовления “Кока - колы” или формулы создания ядерного оружия”, - сказал Р.Ривест на пресс - конференции в 1994 году. Разгадка шифра за такой относительно короткий срок имеет огромное значение для государственных организаций и предпринимателей, которые пользуются аналогичными длинными цифровыми кодами для защиты секретных сведений в своих компьютерных базах данных.



















