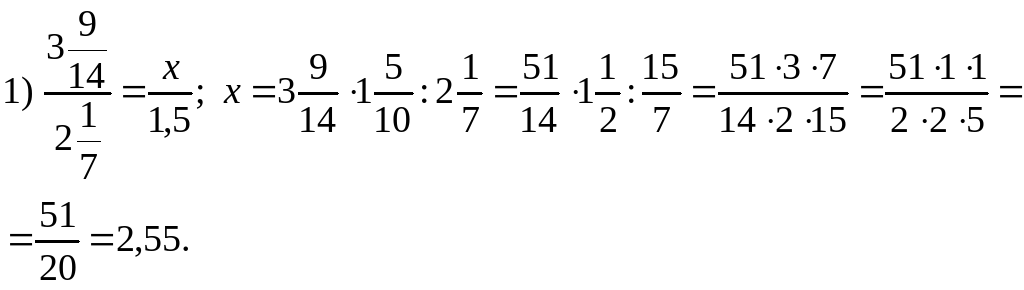Конспект урока по теме "Масштаб"

24 января 2017 г.

Тема урока: Анализ контрольной работы. Масштаб.

Цели:

• ввести понятие масштаба карты;

• показать решение задач с помощью пропорции при заданном масштабе;

• закрепить навык решения уравнений, записанных в виде пропорции.

Ход урока

1. Организационный момент.

2. Анализ контрольной работы.

Разобрать решение заданий контрольной работы № 7, которые вызвали наибольшее затруднение.

1. Устные упражнения.

1. Решить устно № 829 (а; в).

2. Решить № 831 (а; в), вызывая поочередно учащихся к доске для записи пропорций.

Решение.

а) 18 : 2 = 54 : 6; 18 : 54 = 2 : 6; 6 : 2 = 54 : 18; 6 : 54 = 2 : 18.

3. Решить задачу № 835 с помощью пропорции и без пропорции (по действиям).

Двое учащихся решают на доске, остальные на черновиках, затем проверяется решение.

I способ.

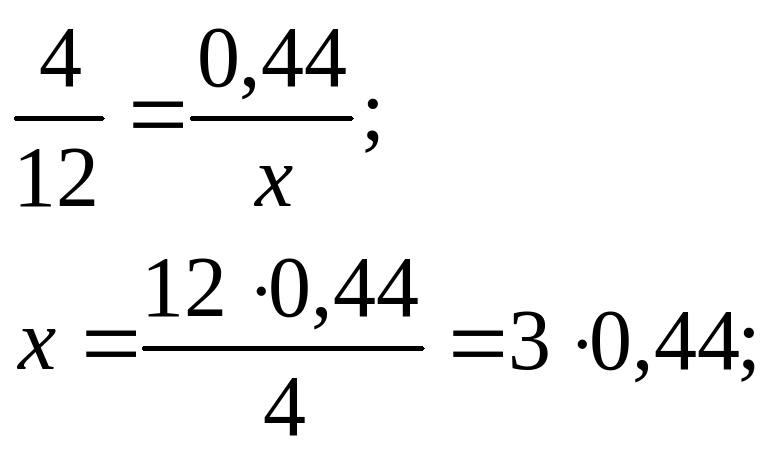
х = 1,32.

Ответ: 1,32 кг картофеля.

II способ.

1) 0,44 : 4 = 0,11 (кг) картофеля на одну порцию запеканки.

2) 0,11 · 12 = 1,32 (кг) потребуется картофеля для 12 порций запеканки.

Ответ: 1,32 кг картофеля.

1. Объяснение нового материала.

1. Участки земной поверхности изображают на бумаге в уменьшенном виде (рис. 35 учебника на с. 134).

2. Определение масштаба карты:

М 1 : 1 00 000 = 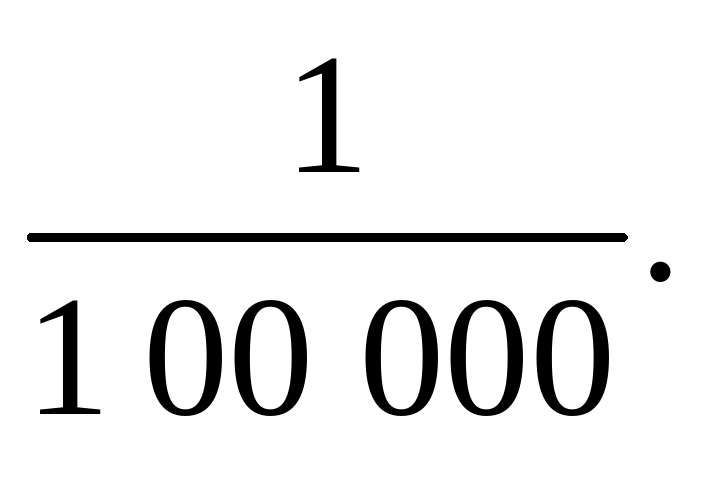Говорят, что карта сделана в масштабе одна стотысячная. Это означает, что 1 см на карте соответствует 1 00 000 см = 1000 м = 1 км на местности.

3. Рассмотреть решение задачи 1.

Длина отрезка на карте 3 см. Масштаб карты М 1 : 1 000 000. Найти длину на местности.

Решение.

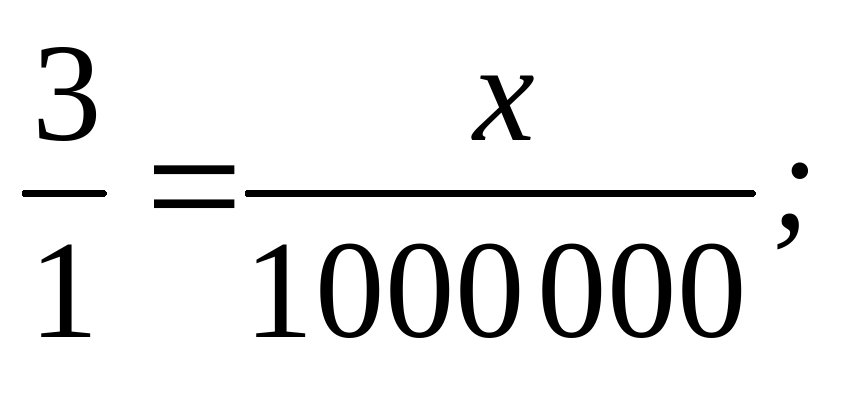
х = 3 · 1 000 000 = 3 000 000 см = 30 000 м = 30 км на местности.

Ответ: 30 км.

4. Рассмотреть решение задачи 2.

Длина отрезка на местности 4,5 км.

М 1 : 100 000. Найти длину отрезка на карте.

Решение.

Обозначим длину (в километрах) отрезка на карте буквой х и составим пропорцию:

х : 4,5 = 1 : 100 000.

х = 4,5 · 1 : 100000 = 0,000045.

Но 0,000045 км = 0,045 м = 4,5 см длина отрезка на карте.

Ответ: 4,5 см.

1. Закрепление изученного материала.

1. Решить задачу № 820, используя рисунок 36 учебника.

2. Решить задачу № 825 на доске и в тетрадях.

Решение.

.

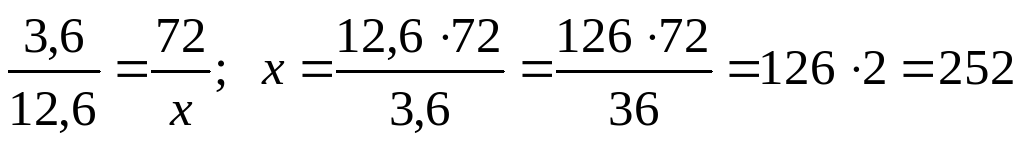Ответ: 252 км.

3. Решить задачу № 821 самостоятельно с проверкой.

4. Решить уравнение № 839 (1) на доске и в тетрадях.

Решение.

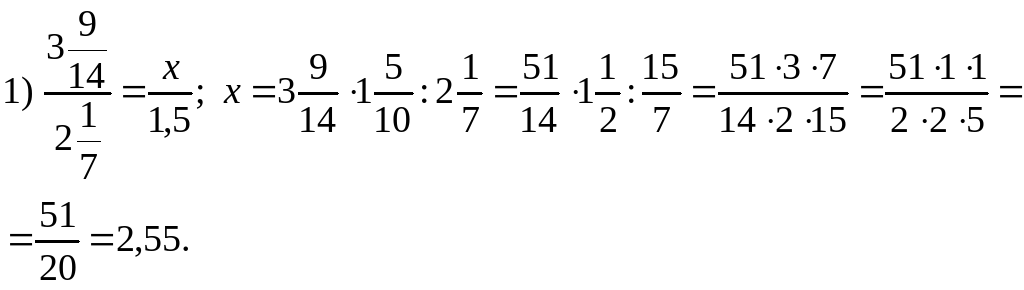
Ответ х = 2,55.

5. Решить задачу № 792 (повторение ранее изученного материала).

Решение.

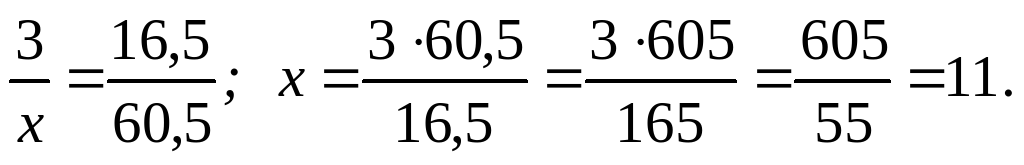
Ответ: 11 дней.

1. Итог урока.

2. Домашнее задание: п. 23; № 840, 843, 846 (б). Принести циркуль.

25 января 2017 г.

Тема урока: Выполнение упражнений по теме Масштаб.

Цели:

• способствовать выработке навыков и умений решения задач, связанных с масштабом;

• развивать логическое мышление учащихся.

Ход урока

1. Организационный момент.

2. Проверка домашнего задания.

3. Повторение изученного материала.

1. Что называют масштабом карты?

2. Чему равен масштаб чертежа, если на нем детали увеличены в 5 раз? уменьшены в 50 раз?

3. Измерить длину и ширину классной комнаты и начертить на доске план этой комнаты в масштабе 1 : 10.

1. Решение задач и уравнений.

1. Решить задачу № 824 по рисунку 37 учебника.

2. Решить задачу № 823.

Решение.

М 1 : 10 000 000; на местности 10 000 000 см = 100 000 м = 100 км; значит, расстояние от Бреста до Владивостока будет соответствовать 100 см на карте, то есть 1 м, поэтому на одной странице тетради это расстояние не уместится.

3. Решить задачу № 827 на доске и в тетрадях с помощью пропорции.

Решение.

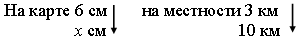
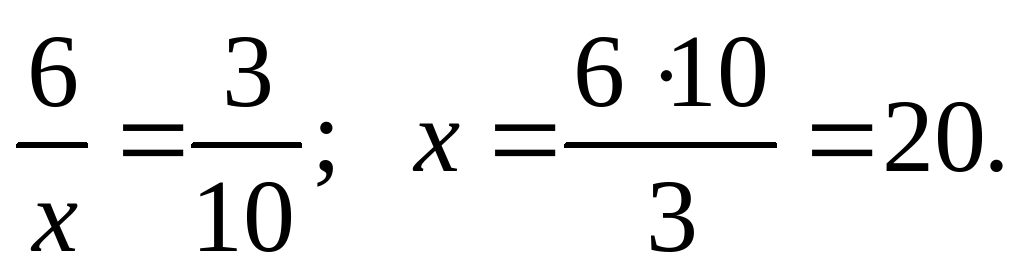
Ответ: 20 см.

4. Решить задачу № 828 (на доске решают два ученика, остальные в тетрадях).

5. Решить задачу № 826 (б) самостоятельно.

Решение.

М 1 : 2 000 000. Это означает, что 1 см на карте соответствует

2 000 000 см = 20 км на местности.

1) 3140 : 20 = 157 (см) на карте.

Ответ: 157 см.

6. Повторение ранее изученного материала.

а) Решить уравнение 7,8 : 2,6 = 4,5 : х.

б) Решить задачу:

На изготовление 14 деталей расходуется 16,8 кг металла. Сколько потребуется металла на изготовление 27 таких деталей?

Решение.

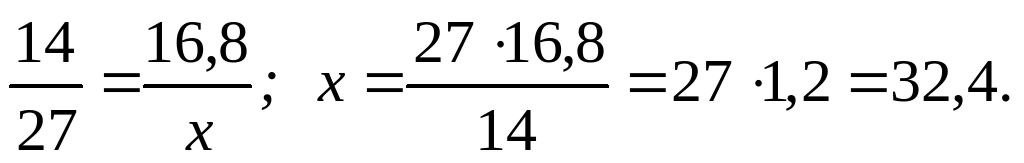
Ответ: 32,4 кг.

в) Решить задачу (самостоятельно с проверкой):

24 человека за 6 дней пропололи участок клубники. За сколько дней выполнят ту же работу 36 человек, если будут работать с такой же производительностью?

Решение.

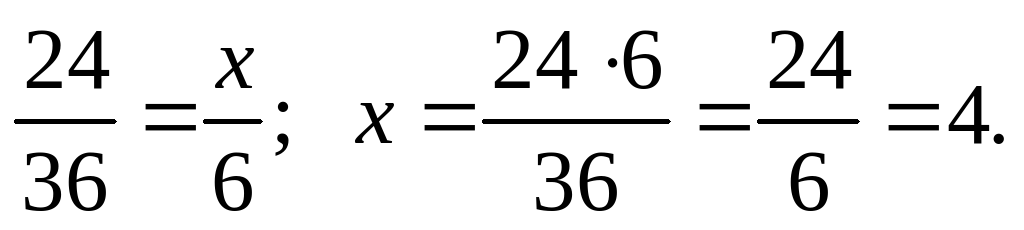
Ответ: 4 дня.

1. Итог урока. Как найти расстояние на местности с помощью карты?

2. Домашнее задание: п. 20–23; решить № 841, 864 (1), 873 (в; г).

25 января 2017 г.

Тема урока: Длина окружности.

Цели:

• ввести понятие окружности и диаметра окружности;

• изучить формулу длины окружности и научить применять ее при решении задач.

Ход урока

1. Организационный момент.

II. Изучение нового материала.

1. Если острие ножки циркуля установить неподвижно в точке О, а другую ножку с грифелем вращать на плоскости листа (или доски), то грифель опишет замкнутую кривую линию, все точки которой будут равноудалены от одной точки О. Эта кривая линия называется окружностью. Точка О называется центром окружности. Отрезок, соединяющий любую точку окружности с ее центром, называется радиусом окружности. Обозначают радиус r. Все радиусы окружности равны между собой.

2. Отрезок, проходящий через центр окружности и соединяющий две ее точки, называется диаметром окружности (d).

Диаметр вдвое больше радиуса (d = 2r). Концы диаметра делят окружность на две равные части.

3. Возьмем круглый стакан, поставим на лист бумаги и обведем его карандашом. На бумаге получится окружность. Если «опоясать» стакан ниткой, а потом распрямить ее, то длина нитки будет приближенно равна длине нарисованной на листе окружности.

4. Длина окружности тем больше, чем больше ее диаметр. Длина окружности прямо пропорциональна длине ее диаметра. Поэтому для всех окружностей отношение длины окружности к длине ее диаметра является одним и тем же числом.

Это отношение обозначают греческой буквой π (читают: «Пи»).

5. Если длину окружности обозначить буквой c, а диаметр – буквой d, то с : d = π, или с = π·d .

Так как d = 2r, то с = π d = 2 π r формула длины окружности.

6. В практических расчетах часто пользуются приближенным значением числа π с точностью до сотых:

π 3,14 (или π ).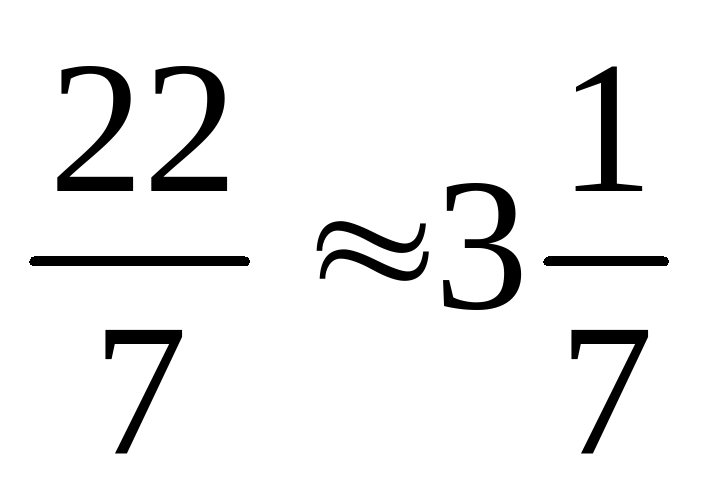

7. (Устно). Вычислить длину окружности, радиус которой 1 см; 10 см; 100 см; 1000 см; 1 м; 2 дм.

III. Закрепление изученного материала.

1. Решить № 849 на доске и в тетрадях.

Решение.

d = 50 см; π 3,1; с = πd  50 · 3,1  135 (см).

Ответ: 135 см.

2. Решить № 847 (три человека решают на доске, остальные самостоятельно в тетрадях, потом проверяется решение).

3. Решить № 850 (выполнить необходимые измерения – измерить диаметр окружности).

Решение.

d = 2,8 см; r = 1,4 см; длина половины окружности равна

π r = 1,4 · 3,14  4,396  4,4 (см).

Ответ: 4,4 см.

4. Решить задачу:

Чтобы определить диаметр ствола дерева, лесник измерил длину окружности ствола дерева. Она равна 3,3 м. Каков диаметр ствола дерева?

Решение.

с = (м).

Ответ: 1,05 м.

5. Повторение ранее изученного материала:

1) решить задачу № 862.

Решение.

1 км = 100 000 см; 10: 100 000 = 1 : 10 000.

Ответ: М 1 : 10 000.

2) Самостоятельно решить № 859 (а; б).

IV. Итог урока.

V. Домашнее задание: п. 24; № 867, 868, 869, 863.