Конспект урока по теме «Наибольшее и наименьшее значение функции»

УРОК ПО АЛГЕБРЕ И НАЧАЛАМ АНАЛИЗА В 11 А КЛАССЕ

ТЕМА «Наибольшее и наименьшее значение функции»

 Тип урока: урок изучения нового материала с использованием ИКТ.

Учитель: Якимова В. А.

Дата проведения: 16.11.2022 г.

Урок по теме «Наибольшее и наименьшее значение функции» продолжает раздел «Применение производной к исследованию функций».

Цель урока: познакомить учащихся с приемами нахождения наибольшего и наименьшего значения функции на интервале и на отрезке, алгоритм нахождения наименьшего и наибольшего значений функции, научить применять алгоритм при решении заданий на отыскание наибольших и наименьших значений функции. Акцентировать внимание учащихся на задачах данной темы, выносимых на экзамен по математике. Создать условия для формирования УУД:

1. Предметные: вспомнить необходимые и достаточные условия существования точек экстремума, понятия: стационарная и критическая точки; вывести алгоритм нахождения наименьшего и наибольшего значений функции, формировать умения решать задачи на отыскание наибольших и наименьших значений функции.

2. Личностные: формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики, развивать интерес у обучающихся к предмету математика. Воспитывать аккуратность, внимательность, умение работать в паре, оценивать работу друг друга.

3. Метапредметные: формировать умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации.

Планируемые результаты: учащийся научится оперировать понятиями «наибольшее значение функции» и «наименьшее значение функции» на интервале и на отрезке, применять алгоритм при решении заданий на отыскание наибольших и наименьших значений функции на отрезке.

Основные понятия: наибольшее (наименьшее) значения функции, стационарная и критическая точки, точки экстремума, алгоритм нахождения наибольшего и наименьшего значений функций.

Технология проведения: фронтальная, индивидуальная работа в сочетании с разными видами самостоятельной деятельности,

дифференцированно - групповая.

Структурные компоненты урока:

1. Организационный этап

2. Постановка формируемых результатов и задач урока. Мотивация учебной деятельности учащихся

3. Проверка домашнего задания

4. Актуализация знаний

5. Изучение нового материала

6. Первичное закрепление нового материала

7. Контроль усвоения

8. Рефлексия учебной деятельности на уроке

9. Информация о домашнем задании

Ход урока

«В мире не происходит ничего,

в чем бы ни был виден смысл

какого-нибудь максимума или минимума!»

Леонард Эйлер

1. Организационный этап

Приветствие. Эпиграф к уроку (слайд 1).

2. Постановка формируемых результатов и задач урока. Мотивация учебной деятельности учащихся

На прошлых уроках мы познакомились с правилами вычисления производных, научились находить производные функций школьной программы и производные сложных функций. Назовите функции, производные которых вы умеете вычислять.

Умеем ли мы находить нахождения наибольшего и наименьшего значения функции на интервале или на отрезке? Значит, тема нашего сегодня урока … (слайд 2).

Нахождение наибольшего и наименьшего значений функции широко применяется при решении многих практических задач, так называемые, задачи на оптимизацию. С некоторыми из таких задач мы познакомимся на следующих уроках. Для этого нам необходимо уметь находить наибольшее и наименьшее значения заданных функций на заданном промежутке.

Постановка обучающимися целей урока (слайд 3).

 3. Проверка домашнего задания

№ 957, № 958, № 959, № 961 (1). Самопроверка. Ребята сравнивают свое решение с решением учителя, причем учитывают аккуратность и логичность решения. Учитель выводит свои решения через veb-камеру на интерактивную доску.

Учащиеся по очереди называют допущенные ошибки и совместно с учителем оценивается домашняя работа.

4. Актуализация знаний

Повторение материала, изученного на предыдущих уроках. Фронтальный опрос (слайд 4). Блиц опрос проводится одновременно с работой учащихся по индивидуальным карточкам у доски (правила дифференцирования, вычисление производной сложных функций).

Блиц опрос:

1) Что называют критической точкой функции?

2) Что обозначает слово «экстремум»?

3) Дайте понятие точки экстремума.

4) Что такое экстремум функции?

5) Какие два понятия объединяет термин «экстремум»?

6) Сформулируйте необходимый признак экстремума.

7) Верно ли утверждение: критическая точка всегда является точкой экстремума?

 8) Когда не является? Приведите пример.

Коллективное решение задачи (слайд 5). Учитель обращает внимание обучающихся на существенное различие понятий максимума (минимума) функций и наибольшего (наименьшего) значений.

1. Найти наибольшее значение функции на отрезке [-1; 3].

2. Найти наименьшее значение функции на отрезке [-1; 3].

Ответ:

Наибольшее значение = 1.

Наименьшее значение = -3.

5. Изучение нового материала

Запишите в тетрадях тему урока «Наибольшее и наименьшее значение функции».

Давайте рассмотрим различные варианты поведения непрерывной на отрезке функции, и попытаемся определить, в каких точках она достигает своего наибольшего и наименьшего значений. (Обсуждение в группах по предложенному плану. Обмен мнениями. Фиксация выводов.)

План обсуждения слайдов:

• Что можно сказать о монотонности функции на отрезке [a; b]?

Ответ: функция возрастает (убывает) на отрезке (слайд 6).

• В какой точке функция достигает своего наибольшего значения?

Ответ: функция имеет на отрезке [a;b] единственную точку экстремума (слайд 7).

• В какой точке функция достигает своего наименьшего значения?

Ответ: …

• Чем можно сказать о данных точках отрезка [a; b]?

Ответ: функция имеет несколько точек экстремума на отрезке [a; b] (слайд 8).

• Какой вывод можно сделать?

Ответ: анализ всех рассмотренных случаев, установление закономерности нахождения наибольшего и наименьшего значения функции на отрезке.

Беседа по слайду 8:

• Где функция может достигать своего максимума на отрезке?

• Какой общий подход к нахождению наибольшего и наименьшего значений функции на отрезке можно применить?

Выводы (слайд 9):

1. Если функция у = f (х) на отрезке [а; b] имеет лишь одну точку, и она является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение.

2. Если функция у = f (х) на отрезке [а; b] не имеет критических точек, то это означает, что на нем функция монотонно возрастает или убывает. Следовательно, свое наибольшее значение функция принимает на одном конце отрезка, а наименьшее – на другом.

3. Если на отрезке [а; b] функция имеет несколько критических точек, то своего наибольшего (наименьшего) значения она достигает либо на концах этого отрезка, либо в критических точках, лежащих на данном отрезке.

Составление алгоритма нахождения наибольшего и наименьшего значений функции на интервале или на отрезке (слайд 10):

1. Найти область определения функции D (f).

2. Найти производную f‘ (x).

3. Найти стационарные и критические точки функции, принадлежащие интервалу (a; b).

4. Найти f (a), f (b) и значения функции в стационарных точках, принадлежащих интервалу (а; b).

5. Среди полученных значений выбрать наибольшее и наименьшее.

6. Первичное закрепление нового материала

Работа по учебнику № 936 (б, в), № 937 (2), № 938 (2, 3).

7. Контроль усвоения

Сегодня мы уже говорили, где применятся задачи по данной теме. Традиционно, задачи, связанные с нахождением наибольшего и наименьшего значения функции на отрезке, включаются в ЕГЭ (11 задание из профильной математики). Давайте попробуем применить полученные знания при решении задач. Индивидуальная работа учащихся с последующей проверкой.

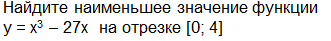1.

2.

3. Найти наибольшее значение функции на отрезке [3; 10]

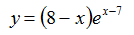
4 . Найти наибольшее значение функции

5. Найти наименьшее значение функции

6. Найти наибольшее значение функции

Проверка решений через veb-камеру с выводом на интерактивную доску (слайды 11 - 16).

8. Рефлексия учебной деятельности на уроке

Ответьте на вопросы:

1. Выполнение каких заданий не вызвало затруднений?

2. При выполнении каких заданий вы ошиблись? Почему?

3. Каковы причины успехов (неудач) вашей деятельности на уроке?

9. Информация о домашнем задании

& 52 стр. 277 - 278, № 936 (а, г), № 938 (1), № 939 (1), № 944.