Ростовская область Родионово-Несветайский район х. Выдел
Муниципальное бюджетное общеобразовательное учреждение
Родионово-Несветайского района
«Выделянская средняя общеобразовательная школа»
Контрольные работы
по алгебре и началам анализа
среднее общее образование 11 класс
Учитель: Лященко Людмила Егоровна
2018-2019 учебный год
Контрольная работа № 1 по теме: « Тригонометрические функции»(А-11)
Вариант 1.
Найти область определения функции: у = 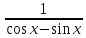
Найти множество значений функции: у = 1 – 4 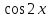 .
.
Найти все корни уравнения 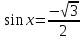 , принадлежащие отрезку
, принадлежащие отрезку 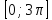 .
.
Найти все решения неравенства 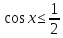 , принадлежащие отрезку
, принадлежащие отрезку 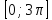 .
.
Найти область определения функции: у= 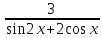 .
.
Контрольная работа № 1 по теме: « Тригонометрические функции»(А-11)
Вариант 1.
Найти область определения функции: у = 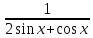 .
.
Найти множество значений функции: у = 1 – 3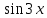 .
.
Найти все корни уравнения 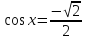 , принадлежащие отрезку
, принадлежащие отрезку 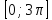
Найти все решения неравенства 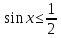 , принадлежащие отрезку
, принадлежащие отрезку 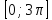 .
.
Найти область определения функции: у= 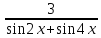 .
.
Контрольная работа № 2
по теме: « Производная и её геометрический смысл».
Вариант 1.
1.Найти производную функции:
а) 0,5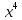 -
- 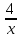 -3
-3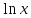 ; б) 3
; б) 3 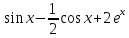 -3;
-3;
в)  +4
+4 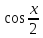 ; г) 3х * (
; г) 3х * ( 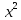 + 4 ); д)
+ 4 ); д) 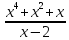 .
.
2.Решить уравнение у (х ) =0, если у (х) = - 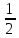 х +
х + 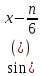 .
.
3.Найти уравнение касательной к графику функции у = (х) в точке с абсциссой 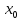 , если (х) =
, если (х) = 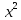 - 3х ,
- 3х , 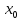 =3.
=3.
4. Решить неравенство: , где у(х) = 2 + 6.
+ 6.
Контрольная работа № 2
по теме: « Производная и её геометрический смысл».
Вариант 2.
1.Найти производную функции:
а) 0,5 -
-  -4
-4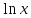 ; б)
; б) 
 -3;
-3;
в)  +2
+2  ; г) 4х * (
; г) 4х * (  + 3 ); д)
+ 3 ); д)  .
.
2.Решить уравнение у (х ) =0, если у (х) = - 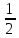 х + .
х + .
3.Найти уравнение касательной к графику функции у = (х) в точке с абсциссой 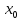 , если (х) = х -3
, если (х) = х -3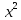 ,
, 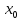 =2.
=2.
4. Решить неравенство: , где у(х) = 
 -
- 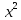 - 3х.
- 3х.
Контрольная работа №3
по теме « Применение производной к исследованию функций».
Вариант 1.
1. Найти точки экстремума функции:
У = 2  + 9
+ 9 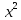 - 24х .
- 24х .
2. Найти наибольшее и наименьшее значения функции:
а) У =  - 3х на отрезке
- 3х на отрезке  .
.
б) у = 2 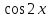 -
-  на отрезке
на отрезке  .
.
3. Исследовать функцию с помощью производной и построить её график:
У =  - 4
- 4 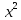 + 3 .
+ 3 .
Контрольная работа №3
по теме « Применение производной к исследованию функций».
Вариант 2.
1. Найти точки экстремума функции:
У = - 3  + 6
+ 6 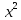 – 5 х .
– 5 х .
2. Найти наибольшее и наименьшее значения функции:
а) У = -  + 9
+ 9 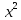 на отрезке
на отрезке  .
.
б) у = 2  -
- 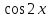 на отрезке
на отрезке  .
.
3. Исследовать функцию с помощью производной и построить её график:
У = -  + 3
+ 3 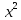 + 5 .
+ 5 .
Контрольная работа № 4 по теме « Интеграл».
Вариант 1.
1. Для функции у (х) найти первообразную, график которой проходит через
точку М:
у (х) = - 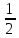
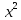 - 3, М
- 3, М  .
.
2. Вычислить интеграл:
а)  - х – 2 ) ∂х ; б)
- х – 2 ) ∂х ; б)  ∂х .
∂х .
3. Вычислить площадь фигуры, ограниченной линиями:
У = 2 - 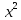 и у = х + 2.
и у = х + 2.
Контрольная работа № 4 по теме « Интеграл».
Вариант 2.
1. Для функции у (х) найти первообразную, график которой проходит через
точку М:
у (х) = 2 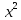 - х , М
- х , М  .
.
2. Вычислить интеграл:
а)  - 3
- 3 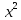 + 2 ) ∂х ; б)
+ 2 ) ∂х ; б)  ∂х .
∂х .
3. Вычислить площадь фигуры, ограниченной линиями:
У =  и у = х + 3 .
и у = х + 3 .
Итоговая контрольная работа.
Вариант 1.
1. Решить уравнение:
 +
+  – 50 = 0 .
– 50 = 0 .
2. Решить уравнение:
 - 1 =
- 1 =  +
+  .
.
3. Решить уравнение:
2  - 2
- 2  + 1=0 .
+ 1=0 .
4. Решить неравенство:
2 +  ≤
≤  .
.
5. Вычислить площадь фигуры, ограниченной линиями:
у = 9 - 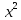 и у =
и у =  - 6х .
- 6х .
Итоговая контрольная работа.
Вариант 2.
1. Решить уравнение:
 -
-  + 35 = 0
+ 35 = 0
2. Решить уравнение:
 - 1 =
- 1 =  +
+  .
.
3. Решить уравнение:
6  - 5
- 5  + 2= 0 .
+ 2= 0 .
4. Решить неравенство:
- 1+  ≥
≥  .
.
5. Вычислить площадь фигуры, ограниченной линиями:
у = 4 - 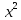 и у =
и у =  + 2х .
+ 2х .







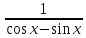
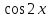 .
.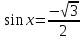 , принадлежащие отрезку
, принадлежащие отрезку 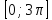 .
.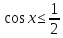 , принадлежащие отрезку
, принадлежащие отрезку 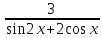 .
.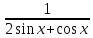 .
.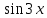 .
.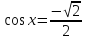 , принадлежащие отрезку
, принадлежащие отрезку 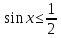 , принадлежащие отрезку
, принадлежащие отрезку 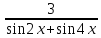 .
.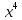 -
- 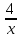 -3
-3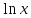 ; б) 3
; б) 3 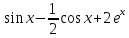 -3;
-3; +4
+4 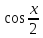 ; г) 3х * (
; г) 3х * ( 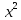 + 4 ); д)
+ 4 ); д) 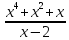 .
.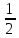 х +
х + 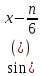 .
.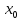 , если (х) =
, если (х) = 









