Презентация к уроку "Два в одном"

Два в одном

«Так много в

математике физики,

как много в физике

математики, и я уже

перестаю находить

разницу между этими

науками.»

А. Эйнштейн

исследование

1

Математические формулы

у = кx + в

2

Физические формулы

1

у = кx

3

y = k/x

V x = V ox + a x t

2

4

3

F x = ma x

у =

5

T = t/N

4

у = ах 2 + вх + с

6

5

у = аsin(кх +в)

x = x 0 + V ox t + a x t 2 /2

6

i = I m sin(wt + α o)

РАЗМИНКА Задача №1

• 1. Материальная точка движется прямолинейно по закону   (где  x  — расстояние от точки отсчета в метрах,  t  — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени  t  = 9 с.

Решение задачи №1. (способ 1)

• Найдем закон изменения скорости:

• При  t  = 9 c имеем:

• Ответ: 60 м/с.

Решение задачи №1. (способ 2)

• Запишем зависимость координаты от времени:

x = x 0 +v 0x . t + a x . t 2 /2

Сравним её с данным законом:

x= 6t 2 - 48t+17

Получим:

v 0x = - 48 м/с ; a x = 12 м/с 2

• Запишем зависимость скорости от времени: v x = v 0x + a x . t При t=9 c имеем:

v x = - 48 м/с +12 м/с 2 . 9c=60 м/с

Ответ: 60 м/с .

Задача №2

• . Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы:  , где  t -  время в минутах, К,    К/мин,    К/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.

Решение задачи №2

• Решение.

Найдем, в какой момент времени после начала работы температура станет равной  1760 К. Задача сводится к

решению уравнения    при заданных значениях параметров  a  и  b :

Через 2 минуты после включения прибор нагреется до 1760 К и при дальнейшем нагревании может испортиться. Таким образом, прибор нужно выключить через 2 минуты.

• Ответ: 2.

Задача №3

• В ходе распада радиоактивного изотопа его масса уменьшается по закону  , где – начальная масса изотопа,   – время, прошедшее от начального момента ,   – период полураспада. В начальный момент времени масса изотопа 40 мг. Период его полураспада составляет 10 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг.

Решение задачи №3. (способ 1)

• Задача сводится к решению неравенства   при заданных значениях параметров    мг и    мин:

• Ответ: 30 мин. 

Решение задачи №3. (способ 2)

Запишем закон радиоактивного распада:

m = m 0 . 2 -t/T Откуда: m/m 0 = 1/2 t/T

5 мг/40 мг= 1/2 t/T

1/8 = 1/2 t/T

1/2 3 = 1/2 t/T

3 = t/T

t = 3 . T = 3 . 10 мин = 30 мин

• Ответ: t = 30 мин.

Задача №4

На рисунке изображены графики зависимости модуля скорости движения четырёх автомобилей от времени. Один из автомобилей за первые 15 с движения проехал наибольший путь. Найдите этот путь. Ответ выразите в метрах.

Решение задачи №4.

Для того чтобы по графику модуля скорости найти путь, пройденный автомобилем за некоторый интервал времени, необходимо вычислить площадь под частью графика, соответствующей этому интервалу времени (в единицах произведения величин, отложенных по осям координат). Из приведенного рисунка видно, что максимальная площадь под графиком за первые 15 с, а значит, и максимальный путь на этом интервале времени, у автомобиля 3.

Найдём его путь, используя формулу для площади трапеции:

Ответ: 187,5 м

Задача №5

Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в кДж.)

Решение задачи №5. (способ 1)

На диаграмме  p-V  работе, совершаемой газом при переходе из начального состояния в конечное, соответствует площадь под линией, изобра-жающей процесс перехода. Для процесса  1-2-3  эта площадь показана на рисунке штриховкой. Таким образом, при переходе из состояния 1 в состояние 3 газ совершает работу

Решение задачи №5. (способ 2)

• При переходе из состояния 1 в состояние 3 газ совершает работу : A / = A / 12 + A / 23
• При изобарном расширении газ совершает работу A / 12 = p . (V 2 - V 1 )= 4 . 10 5 Па . (0,04 м 3 - 0,02 м 3 ) = 8 . 10 3 Дж = 8 кДж
• В изохорном процессе (V = const ) газ работы не совершает: A / 23 = 0
• Следовательно : A / = A / 12 = 8 кДж
• Ответ: 8 кДж.

Основной блок задач

Задача №1

Снаряд массой 4 кг, летящий со скоростью 400 м/с, разрывается на две равные части, одна из которых летит в направлении движения снаряда, а другая - в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличилась на величину ∆E. Скорость осколка, летящего по направлению движения снаряда, равна 900 м/с. Найдите ∆E.

Решение задачи №1

Введем обозначения:  2m — масса снаряда до взрыва; V₀ — модуль скорости снаряда до взрыва; V₁ — модуль скорости осколка, летящего вперед;  V₂— модуль скорости осколка, летящего назад.

Система уравнений для решения задачи:

Выразим  V₂  из первого уравнения:  V₂ = V₁ - 2V₀ и подставим во второе уравнение. Получим:

Отсюда следует:

Ответ: ∆E = 0,5 МДж

Задача №2

В однородном магнитном поле с индукцией  B , направленной вертикально вниз, равномерно вращается в горизонтальной плоскости против часовой стрелки положительно заряженный шарик массой  m , подвешенный на нити длиной  l  (конический маятник). Угол отклонения нити от вертикали равен α, скорость движения шарика равна  v . Найдите заряд шарика  q .

Решение задачи №2

1) На чертеже указаны силы, действующие на шарик.

2) II закон Ньютона в проекциях на оси:

3) Так как   , то выражение для заряда: 

Ответ:  

Задача №3

Камень бросили вертикально вверх с начальной скоростью 15 м/с. Через какое минимальное время после броска потенциальная энергия камня, отсчитанная от уровня точки бросания, будет в 8 раз больше кинетической энергии камня? Сопротивление воздуха пренебрежимо мало.

Решение задачи №3

Запишем уравнения для скорости камня после броска:

Запишем закон сохранения энергии:

Решение данного уравнения:   c

Ответ: 1c

Задача №4

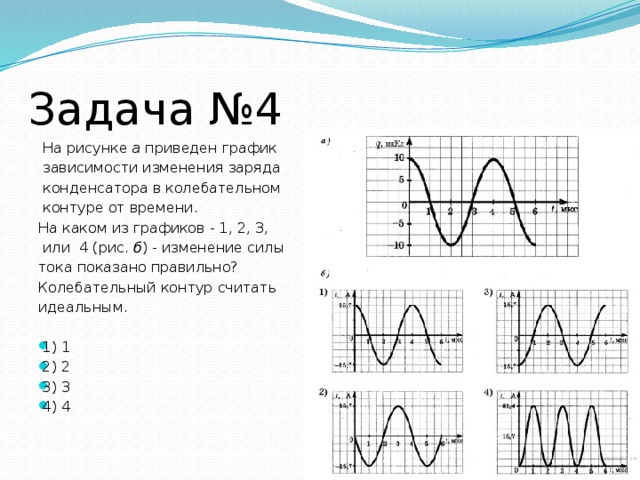
На рисунке  a  приведен график

зависимости изменения заряда

конденсатора в колебательном

контуре от времени.

На каком из графиков - 1, 2, 3,

или 4 (рис.  б ) - изменение силы

тока показано правильно?

Колебательный контур считать

идеальным.

• 1) 1
• 2) 2
• 3) 3
• 4) 4

Решение задачи №4

Из графика на рисунке  a  видно, что амплитуда изменения заряда на конденсаторе равна   , а период колебаний – T = 4мкс. Следовательно, циклическая частота колебаний равна  .

Поскольку в начальный момент времени заряд на конденсаторе максимален и положителен, для закона изменения заряда имеем:  .

Отсюда для закона изменения тока со временем получаем:

Этому закону соответствует график 2.

• Правильный ответ: 2

Задача №5

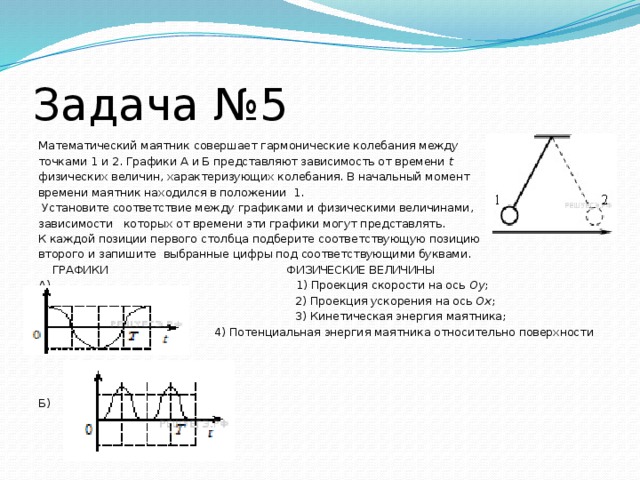
Математический маятник совершает гармонические колебания между

точками 1 и 2. Графики А и Б представляют зависимость от времени  t  

физических величин, характеризующих колебания. В начальный момент

времени маятник находился в положении 1.

Установите соответствие между графиками и физическими величинами,

зависимости которых от времени эти графики могут представлять.

К каждой позиции первого столбца подберите соответствующую позицию

второго и запишите выбранные цифры под соответствующими буквами.

ГРАФИКИ ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) 1) Проекция скорости на ось  Оy ;

2) Проекция ускорения на ось  Ох ;

3) Кинетическая энергия маятника;

4) Потенциальная энергия маятника относительно поверхности земли

Б)

Решение задачи №5

Считая колебания математического маятника малыми, с учётом того, что они начинаются из положения 1, для зависимости координаты маятника от времени имеем

Следовательно, для проекции ускорения получаем:

График А отображает именно такую зависимость от времени. Таким образом, график А соответствует проекции ускорения на ось  Ox  (А - 2). Нули графика соответствуют положению равновесия, а максимумы и минимумы - положениям 1 и 2. Легко видеть, что график Б представляет кинетическую энергию маятника (Б - 3). Действительно,

Максимумы кинетической энергии соответствуют положению равновесия, в котором скорость маятника максимальна, а минимумы - крайним положениям 1 и 2, в которых скорость обращается в ноль.

Практическая задача.

• Собран экспериментальный материал по движению автомобилей. Построить график зависимости расхода топлива от скорости движения. Вывести уравнение этой зависимости и найти оптимальную скорость, при которой наблюдается наименьший расход топлива.

Объекты исследования

1)Hyundai santa fe

3)Nissan almera

3)

2)Hyundai getz

• 4)Nissan murano

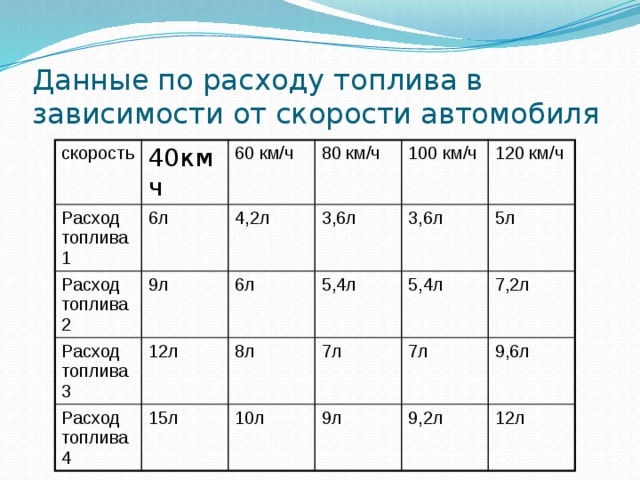
Данные по расходу топлива в зависимости от скорости автомобиля

скорость

40кмч

Расход топлива 1

6л

60 км/ч

Расход топлива 2

9л

80 км/ч

4,2л

Расход топлива 3

12л

3,6л

Расход топлива 4

6л

100 км/ч

5,4л

3,6л

120 км/ч

8л

15л

5л

7л

5,4л

10л

7,2л

7л

9л

9,6л

9,2л

12л

Решение. Данные по расходу топлива в зависимости от скорости автомобиля в координатах

Х

У 1

6

60

У2

9

4,2

У3

80

3,6

12

У 4

100

6

8

15

5,4

3,6

120

5

7

5,4

10

7,2

7

9

9,6

9,2

12

40

График зависимости расхода топлива от скорости автомобиля

Вывод уравнения кривых

1)Hyundai santa fe

-

Квадратичная функция

Ответ.

Определена зависимость между расходом топлива и скоростью автомобиля – квадратичная функция, оптимальная скорость движения при наименьшем расходе топлива 90 км/ч – информация для тех кто ценит свое время и заботится о своем кошельке.