Россия, Омск
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 01.09.2025 12:59
Ноженко Ольга Владимировна
учитель математики
7 лет
3 536
16 717 
Местоположение
Специализация
Медианы, биссектрисы и высоты треугольника
Категория:
Геометрия
20.11.2018 17:48
Просмотр содержимого документа
«Медианы, биссектрисы и высоты треугольника»
Медианы, биссектрисы и высоты треугольника
Нарисуем прямую а и А а. Через точку А проведем в а.
Часть прямой в, а именно отрезок АН называют перпендикуляром проведенным из т А на прямую а.
Точку Н называют основанием перпендикуляра
в
А
а
Н
Теорема: Из точки не лежащей на прямой можно провести к этой прямой перпендикуляр, и притом только один.
(Самостоятельно прочитать док-во из книги)
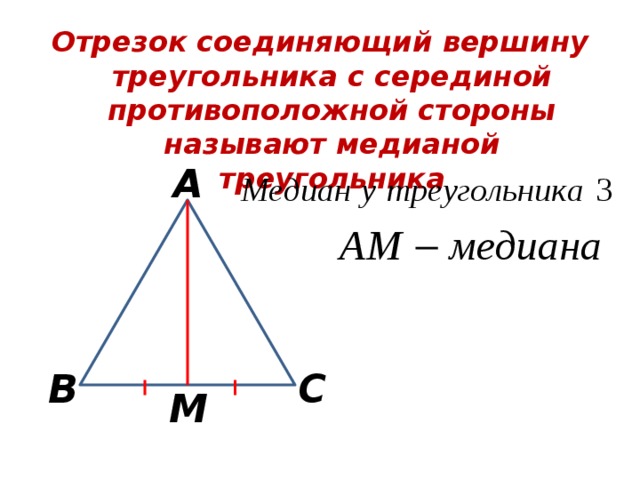
Отрезок соединяющий вершину треугольника с серединой противоположной стороны называют медианой треугольника
А
В
С
М
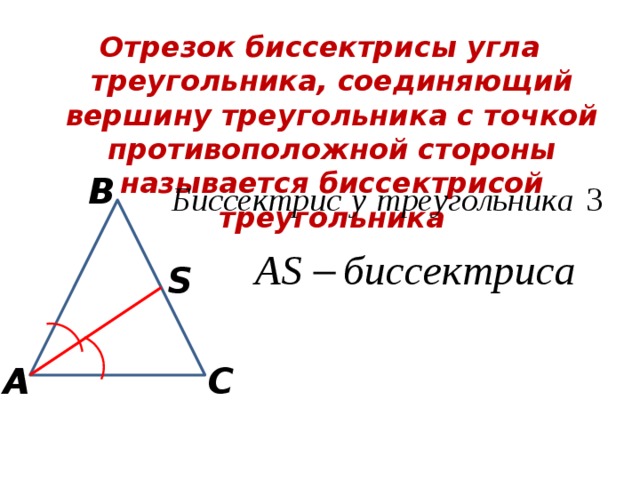
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны называется биссектрисой треугольника
В
S
А
С
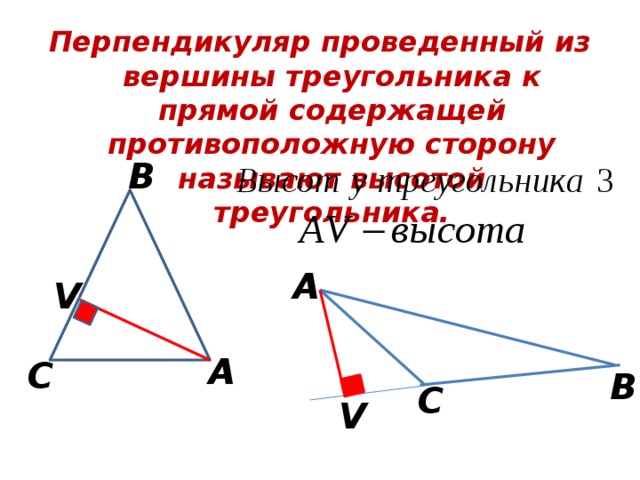
Перпендикуляр проведенный из вершины треугольника к прямой содержащей противоположную сторону называют высотой треугольника.
В
А
V
А
С
В
С
V
Виды треугольников.
В
А
С
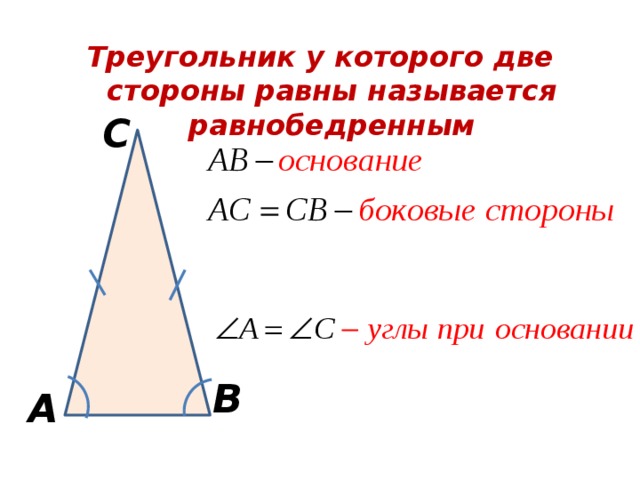
Треугольник у которого две стороны равны называется равнобедренным
С
В
А
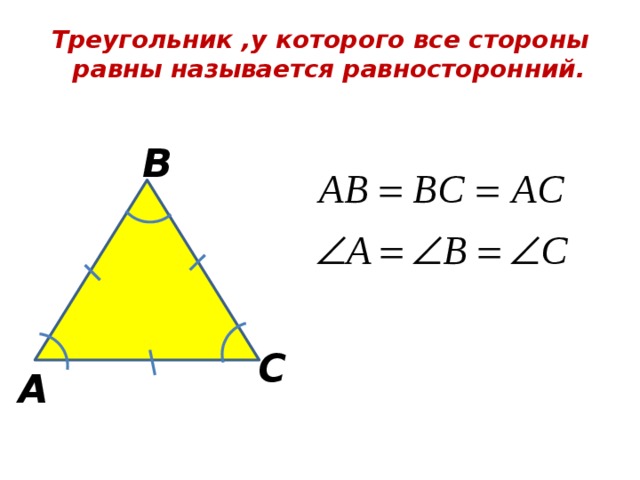
Треугольник ,у которого все стороны равны называется равносторонний.
В
С
А
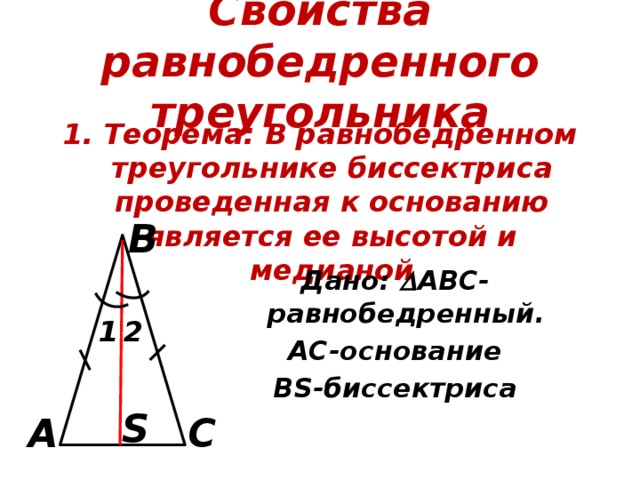
Свойства равнобедренного треугольника
1. Теорема: В равнобедренном треугольнике биссектриса проведенная к основанию является ее высотой и медианой
В
Дано: АВС-равнобедренный.
АС-основание
ВS-биссектриса
1
2
S
А
С
В
Доказать:ВS-медиана, высота
Доказательство:
АВS= SВС по двум сторонам и углу между ними
АВ=ВС, 1= 2(усл) BS-общая.
Из равенства треугольников следует равенство их элементов.
1
2
А
С
S
В
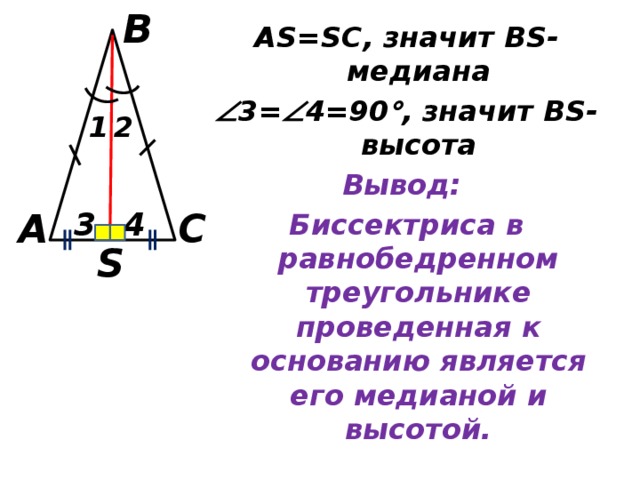
АS=SC, значит BS-медиана
3= 4=90 , значит BS-высота
Вывод:
Биссектриса в равнобедренном треугольнике проведенная к основанию является его медианой и высотой.
1
2
А
4
3
С
S
2. Теорема: В равнобедренном треугольнике углы при основании равны
В
Дано: АВС равнобедренный.
АС основание
Доказать, что А = С
Доказательство:
Проведем ВS-биссектрису, медиану и высоту треугольника.
АВS= SВС по двум сторонам и углу между ними.
2
1
С
А
S
В
Из равенства треугольников следует равенство их элементов.
А= С.
Вывод: Углы при основании равнобедренного треугольника равны
2
1
А
С
S
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
