Просмотр содержимого документа
«Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке»

„ Чтобы стать крылатым, нужно стремление к полёту“
Юрий Алексеевич Гагарин

Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке 12.04.21

Цель урока:
Научить решать задания на нахождение наибольшего и наименьшего значений непрерывной функции на промежутке;
- развивать навыки применения знаний, полученные на уроках математики при решении заданий ЕГЭ;
- повышение познавательной активности у учащихся, развитие логического мышления, математической речи, умения объяснять, анализировать, обобщать и делать выводы;
- контроль навыков решения тестовых заданий в формате ЕГЭ.

Проверка теоретического материала
- Найдите производные функций
1) y=5х 6 ;
1) y=5х 6 ;
2) y=cosx;
2) y=cosx;
А) –sinx
Г)
3) y=
3) y=
4) f(X)=3x 4 -6x+8x 2 ;
4) f(X)=3x 4 -6x+8x 2 ;
Р)
Г)
5) f(X)=(X-6)(x+3)
5) f(X)=(X-6)(x+3)
И)
6) f(X)=sin3x+2cos2x;
6) f(X)=sin3x+2cos2x;
А)
7) f(X)=
7) f(X)=
Н)
![Проверка теоретического материала Найдите по данным таблицы промежутки возрастания и убывания функции, а также точки максимума и точки минимума. x (-∞; -1] f’(x) f(x) -1 + [-1; 0) 0 0 - (0; 2] 0 2 - [2; +∞) 0 +](https://fsd.multiurok.ru/html/2023/02/25/s_63fa679e6f9ef/img4.jpg)
Проверка теоретического материала
Найдите по данным таблицы промежутки возрастания и убывания функции, а также точки максимума и точки минимума.
x
(-∞; -1]
f’(x)
f(x)
-1
+
[-1; 0)
0
0
-
(0; 2]
0
2
-
[2; +∞)
0
+
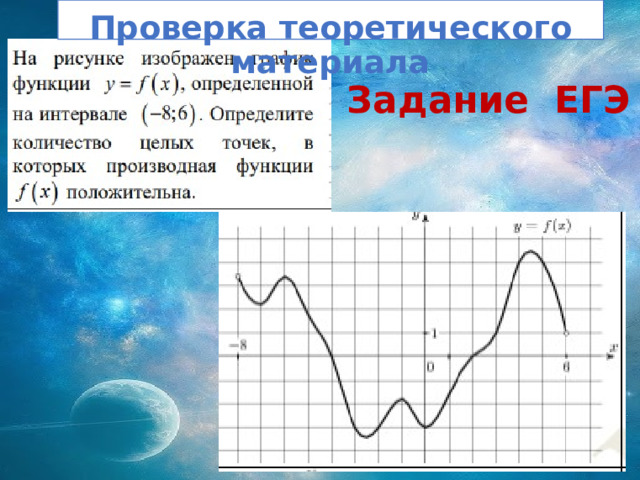
Проверка теоретического материала
Задание ЕГЭ
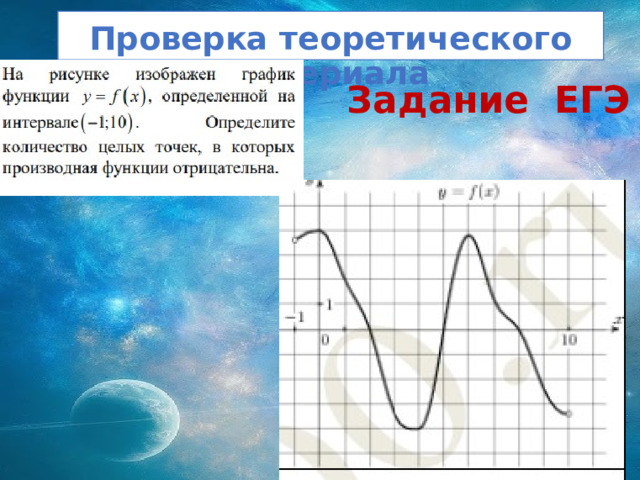
Проверка теоретического материала
Задание ЕГЭ
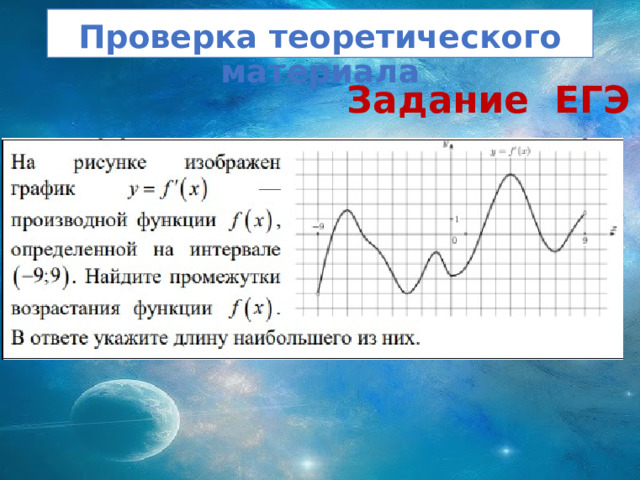
Проверка теоретического материала
Задание ЕГЭ
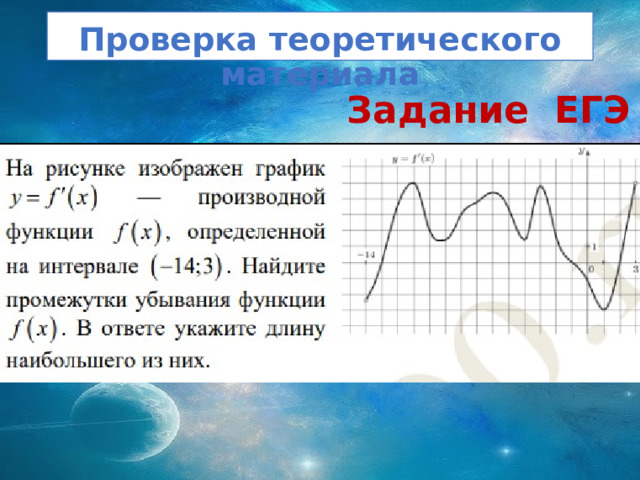
Проверка теоретического материала
Задание ЕГЭ

Проверка теоретического материала
Задание ЕГЭ
- Найдите min и max функции



Задание ЕГЭ
![14 Экспериментальный тур Найти наибольшее значение функции по её графику на [ -7;6] и [ -5;5] у 5 4 2 1 х 6 -5 1 -7 0](https://fsd.multiurok.ru/html/2023/02/25/s_63fa679e6f9ef/img13.jpg)
14
Экспериментальный тур
Найти наибольшее значение функции по её графику
на [ -7;6] и [ -5;5]
у
5
4
2
1
х
6
-5
1
-7
0
![Экспериментальный тур 15 Найти наименьшее значение функции по её графику на [ -7;4] и [-7; 6] у 5 4 2 1 х 1 -5 6 -7 0 3 5](https://fsd.multiurok.ru/html/2023/02/25/s_63fa679e6f9ef/img14.jpg)
Экспериментальный тур
15
Найти наименьшее значение функции по её графику
на [ -7;4] и [-7; 6]
у
5
4
2
1
х
1
-5
6
-7
0
3
5

Экспериментальный тур
парная работа
1) Если функция непрерывна на отрезке, то она достигает на нем и своего наибольшего и своего наименьшего значения.
2) Наименьшего и наибольшего значений непрерывная функция может достигать, как на концах отрезка , так и внутри него.
3) Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.
 0 на (а; b) f(x) – возрастает на [a;b], поэтому наибольшее значение на отрезке функция принимает в правом конце промежутка, а наименьшее в левом конце промежутка. б) если f´(x) левом конце промежутка , а наименьшее в правом конце промежутка . " width="640"
0 на (а; b) f(x) – возрастает на [a;b], поэтому наибольшее значение на отрезке функция принимает в правом конце промежутка, а наименьшее в левом конце промежутка. б) если f´(x) левом конце промежутка , а наименьшее в правом конце промежутка . " width="640"
Если функция y=f(x) не имеет на отрезке[a;b] критических и стационарных точек, тогда
а) если f´(x)0 на (а; b) f(x) – возрастает на [a;b], поэтому наибольшее значение на отрезке функция принимает в правом конце промежутка, а наименьшее в левом конце промежутка.
б) если f´(x) левом конце промежутка , а наименьшее в правом конце промежутка .
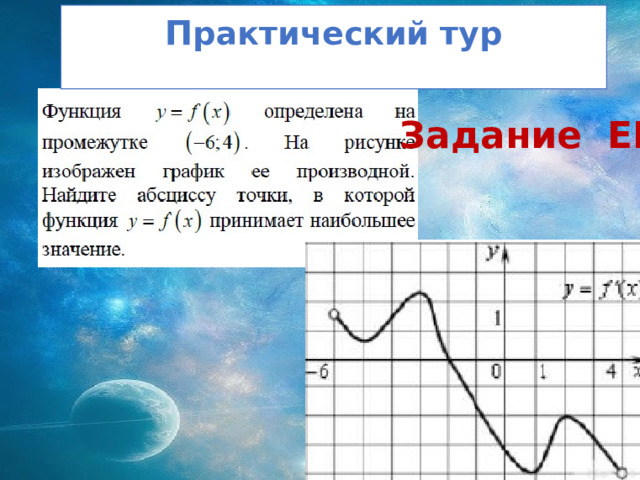
П рактический тур
Задание ЕГЭ
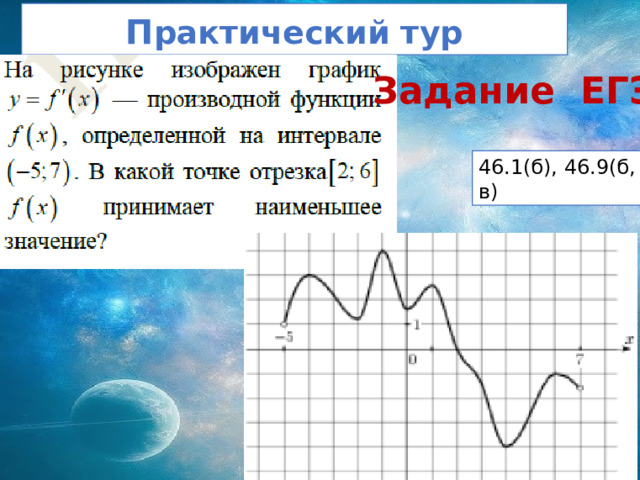
П рактический тур
Задание ЕГЭ
46.1(б), 46.9(б, в)
![Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции на промежутке Найти производную f´(x) Найти стационарные и критические точки функции. Выбрать те, которые лежат внутри отрезка [a;b] Вычислить значения функции y=f(x), в отобранных на третьем шаге и на концах отрезка Выбрать среди этих значений наименьшее (это будет у наим ) и наибольшее (это у наиб )](https://fsd.multiurok.ru/html/2023/02/25/s_63fa679e6f9ef/img19.jpg)
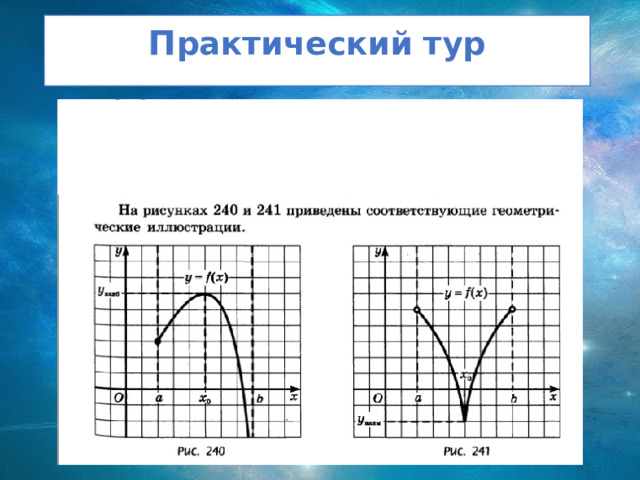
Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции на промежутке
- Найти производную f´(x)
- Найти стационарные и критические точки функции.
- Выбрать те, которые лежат внутри отрезка [a;b]
- Вычислить значения функции y=f(x), в отобранных на третьем шаге и на концах отрезка
- Выбрать среди этих значений наименьшее (это будет у наим ) и наибольшее (это у наиб )
П рактический тур

Домашнее задание
П.46 стр. 369-374 читать), №46.11, 46,14











![Проверка теоретического материала Найдите по данным таблицы промежутки возрастания и убывания функции, а также точки максимума и точки минимума. x (-∞; -1] f’(x) f(x) -1 + [-1; 0) 0 0 - (0; 2] 0 2 - [2; +∞) 0 +](https://fsd.multiurok.ru/html/2023/02/25/s_63fa679e6f9ef/img4.jpg)








![14 Экспериментальный тур Найти наибольшее значение функции по её графику на [ -7;6] и [ -5;5] у 5 4 2 1 х 6 -5 1 -7 0](https://fsd.multiurok.ru/html/2023/02/25/s_63fa679e6f9ef/img13.jpg)
![Экспериментальный тур 15 Найти наименьшее значение функции по её графику на [ -7;4] и [-7; 6] у 5 4 2 1 х 1 -5 6 -7 0 3 5](https://fsd.multiurok.ru/html/2023/02/25/s_63fa679e6f9ef/img14.jpg)

 0 на (а; b) f(x) – возрастает на [a;b], поэтому наибольшее значение на отрезке функция принимает в правом конце промежутка, а наименьшее в левом конце промежутка. б) если f´(x) левом конце промежутка , а наименьшее в правом конце промежутка . " width="640"
0 на (а; b) f(x) – возрастает на [a;b], поэтому наибольшее значение на отрезке функция принимает в правом конце промежутка, а наименьшее в левом конце промежутка. б) если f´(x) левом конце промежутка , а наименьшее в правом конце промежутка . " width="640"


![Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции на промежутке Найти производную f´(x) Найти стационарные и критические точки функции. Выбрать те, которые лежат внутри отрезка [a;b] Вычислить значения функции y=f(x), в отобранных на третьем шаге и на концах отрезка Выбрать среди этих значений наименьшее (это будет у наим ) и наибольшее (это у наиб )](https://fsd.multiurok.ru/html/2023/02/25/s_63fa679e6f9ef/img19.jpg)












