Объем цилиндра.

Определение

Призма — многогранник, составленный из двух равных n -угольников, лежащих в параллельных плоскостях и

n параллелограммов

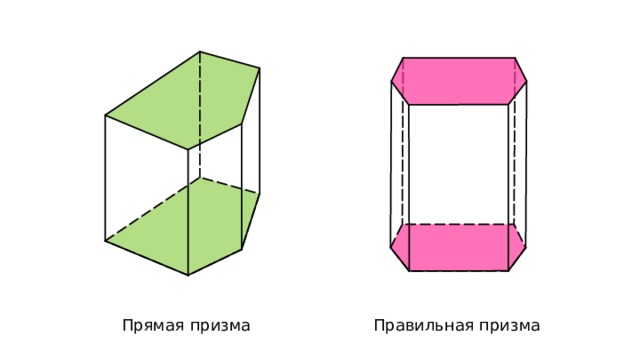
Прямая призма

Правильная призма

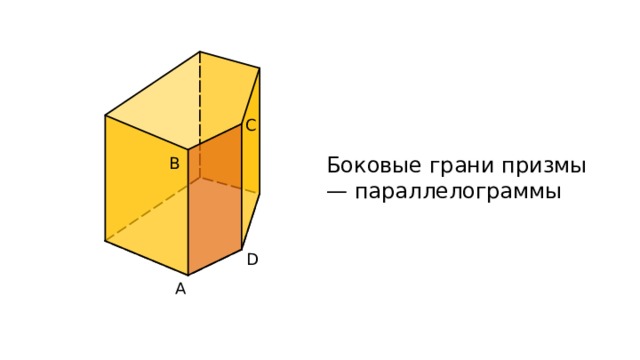
C

Боковые грани призмы — параллелограммы

B

D

А

Теорема

Объём прямой призмы равен произведению площади основания на высоту

V = S осн. · h

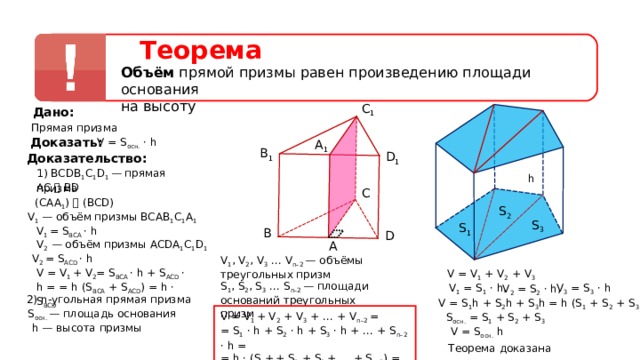
Теорема

Объём прямой призмы равен произведению площади основания

на высоту

C 1

Дано:

Прямая призма

Доказать:

V = S осн. · h

A 1

B 1

D 1

Доказательство:

1) ВС D В 1 С 1 D 1 — прямая призма

h

AC ⏊ BD

С

( CAA 1 ) ⏊ ( BCD )

S 2

V 1 — объём призмы BCAB 1 C 1 A 1

S 3

S 1

V 1 = S BCA · h

B

D

V 2 — объём призмы ACDA 1 C 1 D 1

A

V 2 = S ACD · h  

V 1 , V 2 , V 3 … V n–2 — объёмы треугольных призм

V = V 1 + V 2 = S BCA · h + S ACD · h = = h (S BCA + S ACD ) = h · S BCD

V = V 1 + V 2 + V 3

S 1 , S 2 , S 3 … S n–2 — площади оснований треугольных призм

V 1 = S 1 · h,

V 3 = S 3 · h

V 2 = S 2 · h,

2) n -угольная прямая призма

V = S 1 h + S 2 h + S 3 h = h (S 1 + S 2 + S 3 )

S осн. — площадь основания

V = V 1 + V 2 + V 3 + … + V n–2 =

= S 1 · h + S 2 · h + S 3 · h + … + S n–2 · h =

= h · (S 1 + + S 2 + S 3 + … + S n–2 ) = S осн. · h

S осн. = S 1 + S 2 + S 3

h — высота призмы

V = S oc н. h

Теорема доказана

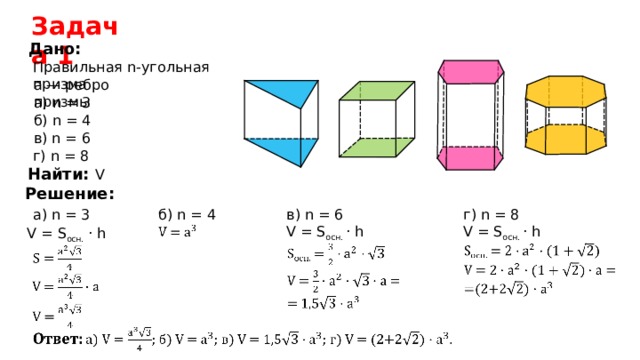
Задача 1

Дано:

Правильная n- угольная призма

а — ребро призмы

а ) n = 3

б) n = 4

в) n = 6

г) n = 8

Найти: V

Решение:

в ) n = 6

г ) n = 8

a) n = 3

б ) n = 4

V = S осн. · h

V = S осн. · h

V = S осн. · h

Задача 2

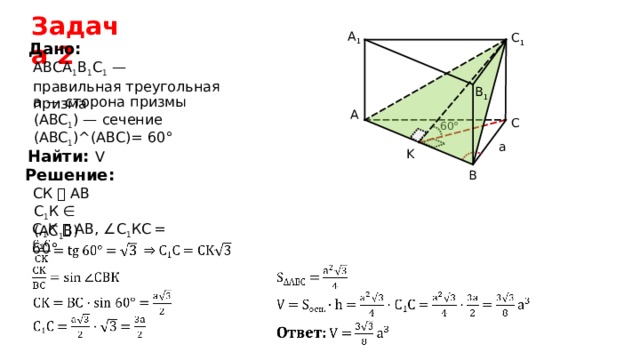
A 1

C 1

Дано:

АВСА 1 В 1 С 1 —

правильная треугольная призма

B 1

а — сторона призмы

A

(ABC 1 ) — сечение

C

60°

(ABC 1 )^( АВС ) = 60°

a

K

Найти: V

Решение:

B

СК ⏊ АВ

С 1 К ∈ (AC 1 B)

С 1 К ⏊ АВ, ∠С 1 КС = 60°