
Учитель математики МБОУ СОШ № 49,г. Новокузнецка
Сухова Людмила Васильевна
Тема урока: «Однородные тригонометрические уравнения» 10класс.
Тип урока: сознательное усвоение нового материала.
Ход урока
I.Организационный момент.
Учитель сообщает цели урока, проводит вводную беседу. ( В течение 5 уроков мы с вами решали тригонометрические уравнения, используя различные методы их решения). Выяснили, что правильно выбранный метод позволяет упростить решение. Сегодня мы познакомимся с еще одним видом тригонометрических уравнений, а пока перед вами стоит задача – показать свои знания и умения в решении тригонометрических уравнений.
II. Воспроизведение и коррекция опорных знаний.
Устная работа.
А) Какое уравнение мы называем тригонометрическим?
Б) Назовите алгоритм решения уравнения cost = а?
1. Проверить условие | a | ≤ 1
2. Отметить точку, а на оси абсцисс.
3. Построить перпендикуляр в этой точке.
4. Отметить точки пересечения перпендикуляра с окружностью
5. Полученные точки – решение уравнения cost = a.
6. Записать общее решение уравнения:
t =  arccosa +2
arccosa +2 ,
, k
k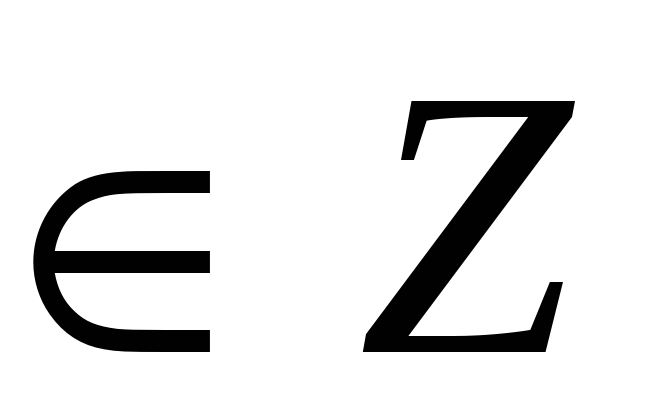 .
.
7. Какие особые случаи решения уравнения вы знаете?
а) cost=1, t= 2 , б) cost= -1, t=
, б) cost= -1, t=  + 2
+ 2 cost = 0, t =
cost = 0, t =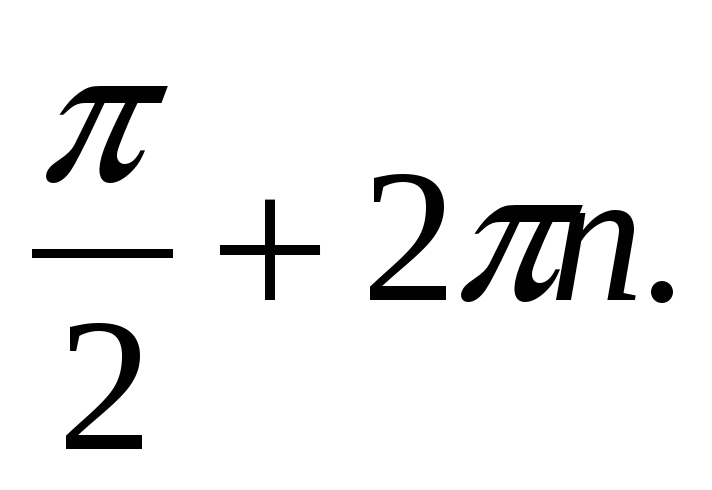
8. Если, а отрицательное число, как записать решение этого уравнения?
t =  (
(  - arccosa) +2
- arccosa) +2 ,
, k
k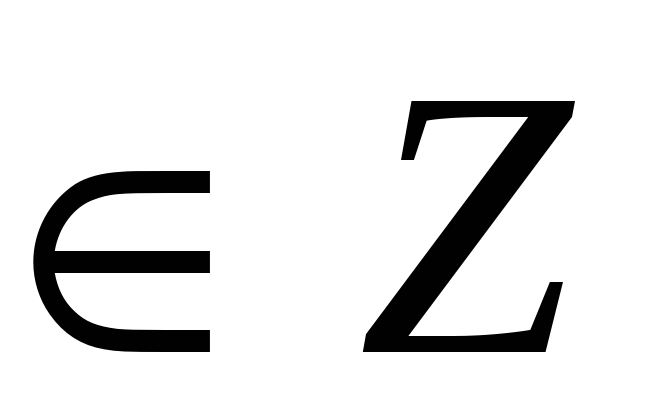 .
.
В. Назовите алгоритм решения уравнения sin t = а?
1. Проверить условие | a | ≤ 1
2. Отметить точку, а на оси ординат.
3. Построить перпендикуляр в этой точке.
4. Отметить точки пересечения перпендикуляра с окружностью
5. Полученные точки – решение уравнения . sint = a.
6. Записать общее решение уравнения.
t1 = arcsina +2 ,
, k
k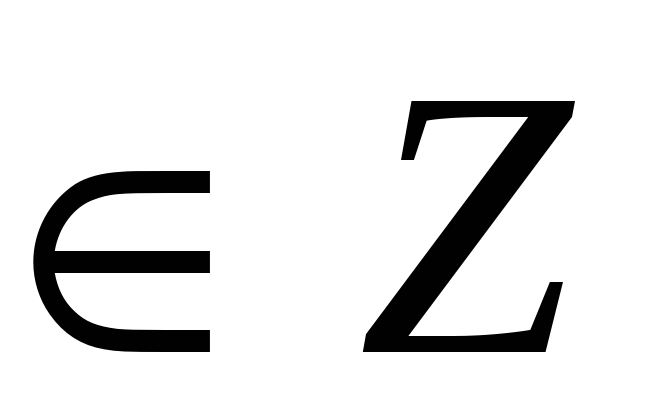 .
.
t2 =  - arcsina +2
- arcsina +2 ,объединяя эти решения имеем:
,объединяя эти решения имеем:
t = (-1)k arcsina + ,
,
7. Какие особые случаи решения уравнения вы знаете?
а) sint=1 t= 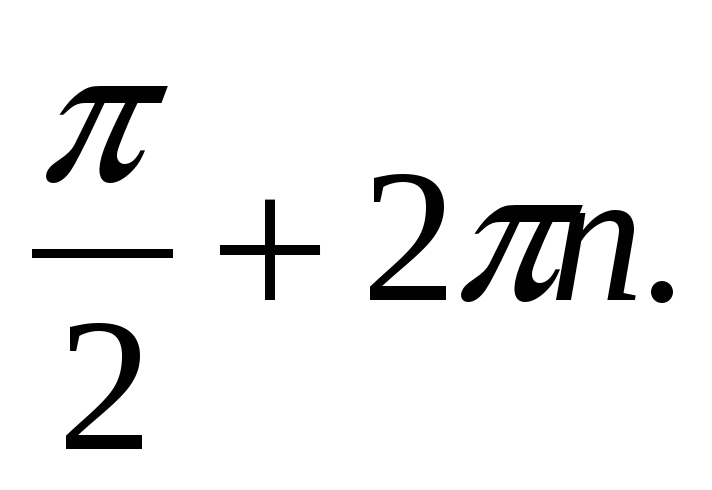 б) sint = -1, t= -
б) sint = -1, t= -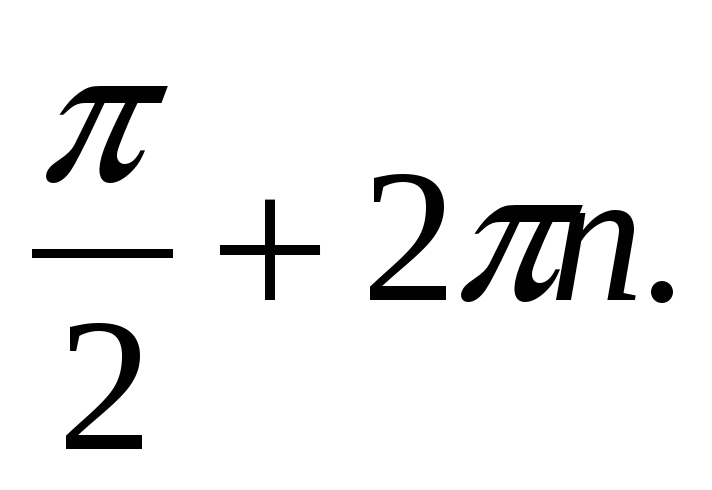 в) sint=0 t=
в) sint=0 t= n
n
8. Если а отрицательное число, как записать решение этого уравнения?
t = (-1)k+1 arcsina + ,
, k
k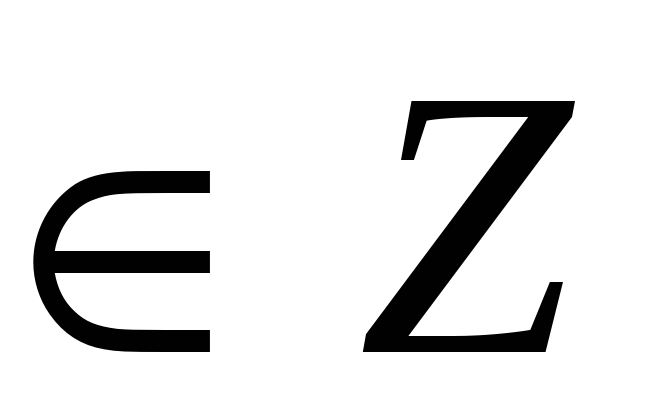 .
.
III.Устно:
Решить уравнения:
а)sin x =; б)2sin x =2; в)sin 2x =0; г)3cosx = -3; д) tgx =1; е) cosx= 2,5.
Вычислить: arccos; : arcos(-); : arccos; : arccos1 ; arcsin;
arcsin(-); arctg1; arctg(-).
Имеют ли смысл выражения:
а) arccos 5; arccos ; arctg3; arcsin(-2); arcсtg(-7).?
IV. Этап подготовки учащихся к активному и сознательному усвоению нового материала.
Расскажите способ решения уравнения:
а). 2 sin2 x +5 sin x -3 =0 (Замена на sin x =а, где  IaI 1)
IaI 1)
б). 3tgx +5ctgx -8=0 (ctgx заменяем на tgx и сводим к квадратному)
в). 2sin 2x +5cosx +1=0 (sin 2x заменяем через 1- cos2 x, и сводим к квадратному)
г).(tgx-)(cosx-1)=0 (разложением на множители)
д). cos2 x os2x -3 cosx =0. (разложением на множители).
е). 5 sin x + 2cosx =0
Какое уравнение вызывает трудность?(е)
Сегодня мы познакомимся с еще одним видом тригонометрических уравнений, которые получили специальное название.
V. Этап усвоения новых знаний:
Открыли тетради, записали число и тему урока: «Однородные тригонометрические уравнения»
Уравнение: 5 sin x + 2cosx =0 получило специальное название.
Рассмотрим решение данного уравнения.
Разделим почленно обе части уравнения на cosx0, имеем
5tgx +2 =0; tgx = 0,4; х = -arctg0,4 + k, kz
k, kz
VI. Закрепление нового материала :
Рассмотреть у доски решение уравнений:
а) sin x + cosx =0 б) sin2 x - cos2x =0
VII. Этап проверки понимания учащимися нового материала:
Как вы думаете, будет ли однородным уравнение :
sin 2x +cos2x =0
sin x + cosx = 2
sin2 x - 3sin x cosx +2cos2x =0( да будет, т.к. каждый член этого уравнения имеет вторую степень) Как будем решать данное уравнение?( Делением на cos2x 0)
sin2 x - 3sin x cosx +2cos2x =0
tg2 x - 3tgx +2 =0 , а1 =2 и а2 =1, tgx=2; х = arctg2 +z
tgx =1, х = arctg1 +z; x =,.
Решить у доски еще одно уравнение: 3sin2 2x +sin 2x cos2x – 2cos2 2x =0
3tg22x +tg2x -2 =0 , а1 = и а2 =-1, tg2x=; 2х = arctg +z ,
х = arctg +, tgx =-1, x =-,.
VIII. Этап всесторонней проверки знаний:
Самостоятельная работа в форме тестированного контроля.
Дифференцированные задания по двум вариантам. ( учащимся предлагается выбрать правильный ответ). Подведение итогов на экране.
Самостоятельная работа
| - вариант | А | Б | В |
| 1). sin x + 2cosx =0 | x = -arctg2+ k, k k, k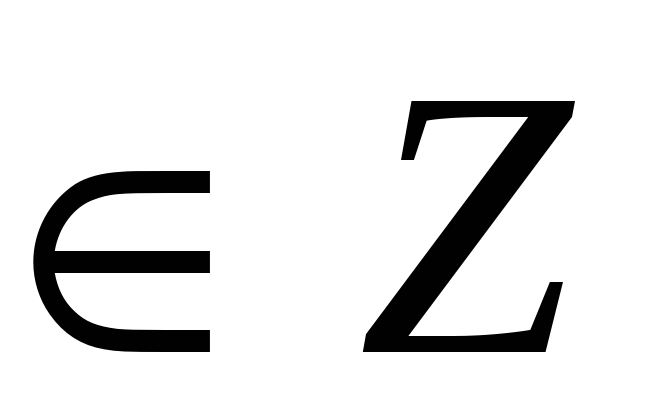 . . | x = arctg2+ k, k k, k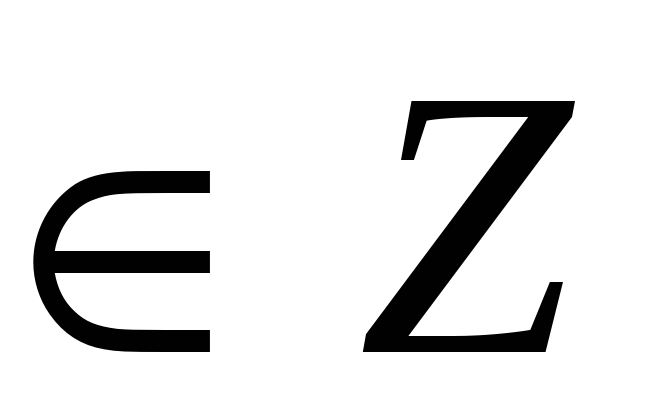 . . | Корней нет |
| 2).sin2 x+2sin x cosx -3cos2x =0 | x = -+ x = -arctg3+ k k k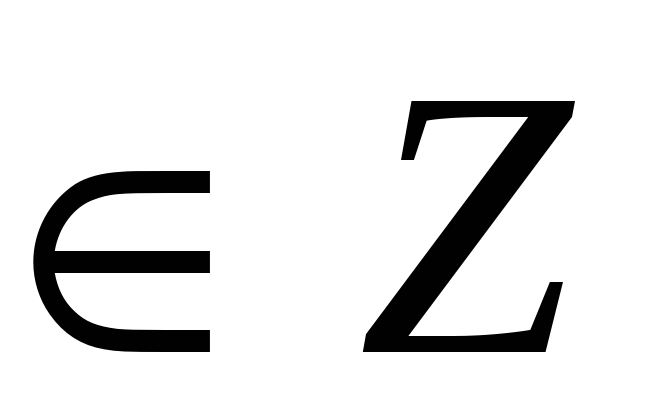 | x = + x = arctg3+ k k k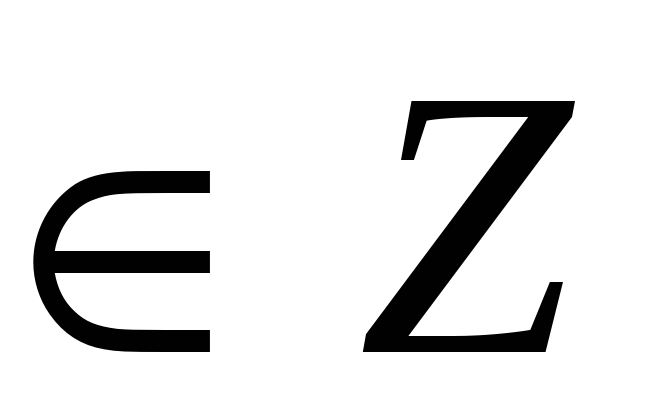 | x = + x = -arctg3+ k k k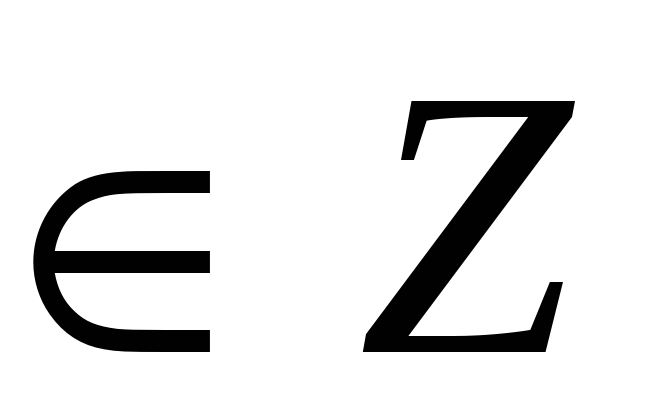
|
| -вариант |
| 1). sin x - 4cosx =0 | x = arctg+ k k k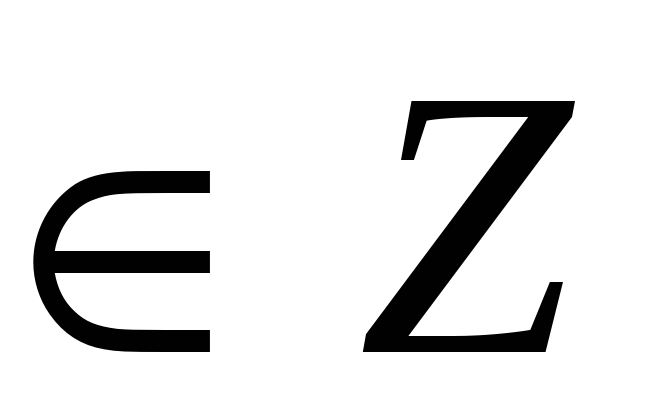 | Корней нет | x = arctg4+ k k k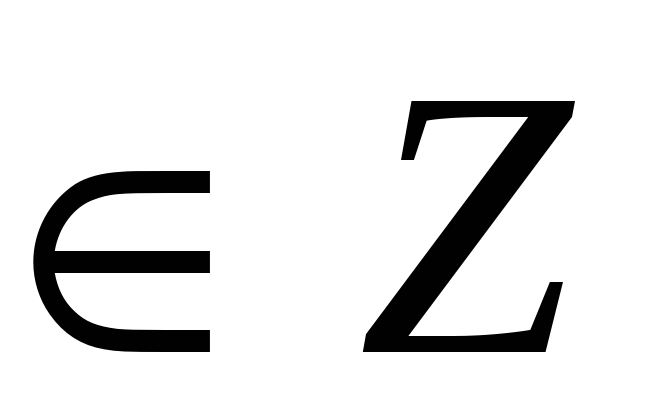 |
| 2).sin2 x-4sin x cosx +3cos2x =0 | x = + x = arctg3+ k k k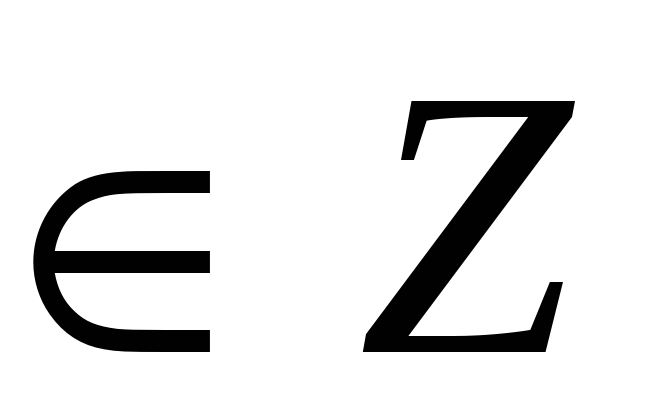 | x = -+ x = arctg3+ k k k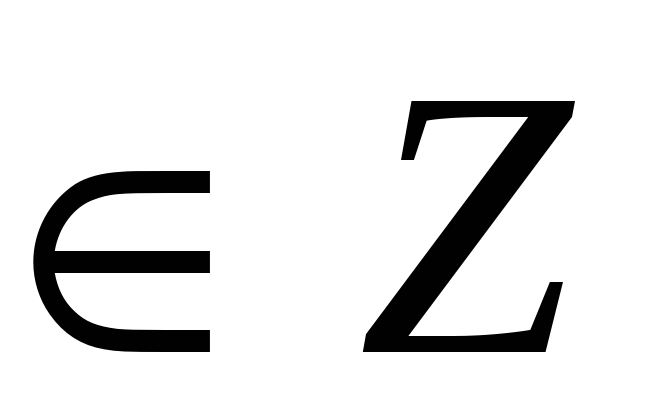 | x = + x = -arctg3+ k k k |
Разобрать решение уравнения:
5sin2 x -14 sin x cosx – 3cos2x =2 (представим 2(sin2 x + cos2x) в виде суммы квадрата тригонометрических функций)
5sin2x -14 sin x cosx – 3cos2x =2
5sin2x -14 sin x cosx – 3cos2x =2 (sin2 x + cos2x)
3sin2 x - 14sin x cosx -5cos2x =0/ cos2x
3tg2 x - 14tgx -5 =0; а1 =5 и а2 =-, tgx =5; х = arctg5 +z
tgx =-, х = -arctg +z;
Ответы к самостоятельной работе:
IX. Подведение итогов, выставление оценок.
1. C каким видом уравнения мы познакомились на этом уроке?
2. Какие уравнения мы называем однородными?
3.Расскажите, как решаются однородные уравнения?
4. Как вы думаете, почему мы так много решаем тригонометрических уравнений?

















