На рисунке изображен план сельской местности.
Таня на летних каникулах приезжает в гости к дедушке в деревню Антоновка (на плане обозначена цифрой 1). В конце каникул дедушка на машине собирается отвезти Таню на автобусную станцию, которая находится в деревне Богданово. Из Антоновки в Богданово можно проехать по проселочной дороге мимо реки. Есть другой путь — по шоссе до деревни Ванютино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Богданово. Третий маршрут проходит по проселочной дороге мимо пруда до деревни Горюново, где можно свернуть на шоссе до Богданово. Четвертый маршрут пролегает по шоссе до деревни Доломино, от Доломино до Горюново по проселочной дороге мимо конюшни и от Горюново до Богданово по шоссе. Еще один маршрут проходит по шоссе до деревни Егорка, по проселочной дороге мимо конюшни от Егорки до Жилино и по шоссе от Жилино до Богданово.
Шоссе и проселочные дороги образуют прямоугольные треугольники.
По шоссе Таня с дедушкой едут со скоростью 50 км/ч, а по проселочным дорогам — со скоростью 30 км/ч. Расстояние от Антоновки до Доломино равно 12 км, от Доломино до Егорки — 4 км, от Егорки до Ванютино — 12 км, от Горюново до Ванютино — 15 км, от Ванютино до Жилино — 9 км, а от Жилино до Богданово — 12 км.
Пользуясь описанием, определите, какими цифрами на плане обозначены деревни. В ответ запишите последовательность четырех цифр без пробелов, запятых и других дополнительных символов.
| Деревни | Ванютино | Горюново | Егорка | Жилино |
| Цифры |
|
|
|
|
2. Тип 2 № 408366 
Найдите расстояние от Антоновки до Егорки по шоссе. Ответ дайте в километрах.
3. Тип 3 № 408370 
Найдите расстояние от Егорки до Жилино по прямой. Ответ дайте в километрах.
4. Тип 4 № 408374 
Сколько минут затратят на дорогу Таня с дедушкой из Антоновки в Богданово, если поедут мимо пруда через Горюново?
5. Тип 5 № 408378 
За какое наименьшее количество минут Таня с дедушкой могут добраться из Егорки в Жилино?
6. Тип 6 № 340581 
Найдите значение выражения
7. Тип 7 № 317179 
На координатной прямой отмечены числа x и y. Какое из следующих утверждений об этих числах верно?
В ответе укажите номер правильного варианта.
1) и
2) и
3) и
4) и
8. Тип 8 № 383598 
Найдите значение выражения
9. Тип 9 № 316225 
Решите уравнение:
10. Тип 10 № 311767 
Стас, Денис, Костя, Маша, Дима бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должна будет девочка.
11. Тип 11 № 193089 
Найдите значение a по графику функции изображенному на рисунке.
12. Тип 12 № 311920 
Центростремительное ускорение при движении по окружности (в м/c2 ) можно вычислить по формуле где — угловая скорость (в с−1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 3 с−1, а центростремительное ускорение равно 45 м/c2.
13. Тип 13 № 338499 
Решите неравенство
В ответе укажите номер правильного варианта.
1) (− ∞; +∞)
2) (− ∞; −6)∪(6; +∞)
3) (− 6; 6)
4) нет решений
14. Тип 14 № 394400 
Кругами одинакового радиуса заполнили правильный треугольник (см. рис.), а потом тем же количеством кругов — прямоугольник. Найдите количество кругов, если известно, что и на стороне треугольника, и на большей стороне прямоугольника располагается на два круга больше, чем на меньшей стороне прямоугольника.
15. Тип 15 № 339406 
Площадь прямоугольного треугольника равна Один из острых углов равен 30°. Найдите длину катета, прилежащего к этому углу.
16. Тип 16 № 311479 
Прямоугольный треугольник с катетами 5 см и 12 см вписан в окружность. Чему равен радиус этой окружности?
17. Тип 17 № 324017 
Сторона ромба равна 9, а расстояние от центра ромба до нее равно 1. Найдите площадь ромба.
18. Тип 18 № 323750 
Площадь одной клетки равна 1. Найдите площадь фигуры, изображенной на рисунке.
19. Тип 19 № 341676 
Какие из следующих утверждений верны?
1) Треугольника со сторонами 1, 2, 4 не существует.
2) Смежные углы равны.
3) Все диаметры окружности равны между собой.
Если утверждений несколько, запишите их номера в порядке возрастания.
20. Тип 20 № 311591 
Решите уравнение:
21. Тип 21 № 311659 
Пристани и расположены на реке, скорость течения которой на этом участке равна 3 км/ч. Лодка проходит туда и обратно без остановок со средней скоростью 8 км/ч. Найдите собственную скорость лодки.
22. Тип 22 № 338295 
Постройте график функции и определите, при каких значениях m прямая имеет с графиком ровно одну общую точку.
23. Тип 23 № 182 
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 2. Найдите площадь трапеции.
24. Тип 24 № 349626 
Окружности с центрами в точках P и не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении a:b. Докажите, что диаметры этих окружностей относятся как a:b.
25. Тип 25 № 311926 
В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь ч
В течение года абонент пользовался тарифом «Стандартный», абонентская плата по которому составляла 350 рублей в месяц. При условии нахождения абонента на территории РФ в абонентскую плату тарифа «Стандартный» входит:
• пакет минут, включающий 300 минут исходящих вызовов на номера, зарегистрированные на территории РФ;
• пакет интернета, включающий 3 гигабайта мобильного интернета;
• пакет СМС, включающий 120 СМС в месяц;
• безлимитные бесплатные входящие вызовы.
Стоимость минут, интернета и СМС сверх пакета тарифа указана в таблице.
| Исходящие вызовы | 3 руб./мин. |
| Мобильный интернет (пакет) | 90 руб. за 0,5 Гб |
| СМС | 2 руб./шт. |
Абонент не пользовался услугами связи в роуминге. За весь год абонент отправил 110 СМС.
Определите, какие месяцы соответствуют указанному в таблице трафику мобильного интернета.
Заполните таблицу, в бланк ответов перенесите числа, соответствующие номерам месяцев, без пробелов, запятых и других дополнительных символов (например, для месяцев май, январь, ноябрь, август в ответе нужно записать число 51118).
| Мобильный интернет | 2,5 Гб | 3 Гб | 3,25 Гб | 1 Гб |
| Номер месяца |
|
|
|
|
2. Тип 2 № 406564 
Сколько рублей потратил абонент на услуги связи в июне?
3. Тип 3 № 406675 
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику израсходованных минут и гигабайтов.
| ПЕРИОДЫ | | ХАРАКТЕРИСТИКИ |
| А) январь−февраль Б) февраль−март В) август–сентябрь Г) ноябрь–декабрь | | 1) Расход минут увеличился, а расход гигабайтов уменьшился. 2) Расход гигабайтов увеличился, а расход минут уменьшился. 3) Расход минут увеличился, и расход гигабайтов увеличился. 4) Расход минут уменьшился, и расход гигабайтов уменьшился. |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
4. Тип 4 № 406565 
Какое наименьшее количество минут исходящих вызовов за месяц было в 2019 году?
5. Тип 5 № 406659 
Абонент хочет приобрести новый смартфон. В трех салонах сотовой связи этот смартфон продается в кредит (сначала делается первоначальный взнос, а потом ежемесячно в течение всего срока кредита вносятся платежи) на разных условиях. Условия приведены в таблице.
| Салон | Стоимость смартфона (руб.) | Первоначальный взнос (в % от стоимости) | Срок кредита (мес.) | Ежемесячный платеж (руб.) |
| А | 18 000 | 20 | 6 | 2650 |
| Б | 17 500 | 30 | 12 | 1200 |
| В | 17 600 | 25 | 12 | 1300 |
Определите, в каком из салонов покупка обойдется дешевле всего (с учетом переплаты). В ответ запишите эту сумму в рублях.
6. Тип 6 № 333006 
Найдите значение выражения
7. Тип 7 № 205774 
О числах a, b, c и d известно, что . Сравнитe числа d и a.
В ответе укажите номер правильного варианта.
1)
2)
3)
4) Сравнить невозможно
8. Тип 8 № 316344 
Сократите дробь
9. Тип 9 № 338202 
Квадратный трехчлен разложен на множители: Найдите
10. Тип 10 № 132744 
Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 15 с машинами и 10 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Толе достанется пазл с машиной.
11. Тип 11 № 311676 
Установите соответствие между графиками функций и формулами, которые их задают.
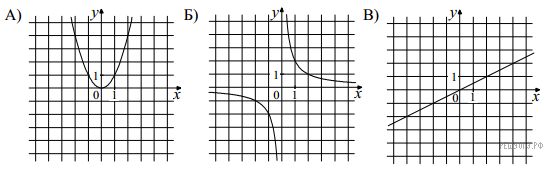
1)
2)
3)
4)
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
12. Тип 12 № 311530 
Площадь трапеции можно вычислить по формуле где — основания трапеции, h — высота (в метрах). Пользуясь этой формулой, найдите высоту h, если основания трапеции равны и а ее площадь
13. Тип 13 № 338497 
На каком из рисунков изображено решение неравенства
В ответе укажите номер правильного варианта.
1) 1
2) 2
3) 3
4) 4
14. Тип 14 № 394420 
Каждый день больной заражает четырех человек, каждый из которых, начиная со следующего дня, каждый день также заражает новых четырех и так далее. Болезнь длится 14 дней. В первый день месяца в город N приехал заболевший гражданин К, и в это же день он заразил четырех человек. В какой день станет 3125 заболевших? (В ответе укажите только число.)
15. Тип 15 № 193 
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.
16. Тип 16 № 339429 
Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC = 15° и ∠OAB = 8°. Найдите угол BCO. Ответ дайте в градусах.
17. Тип 17 № 169862 
Сторона квадрата равна 10. Найдите его площадь.
18. Тип 18 № 40 
Найдите тангенс угла AOB, изображенного на рисунке.
19. Тип 19 № 401818 
Какие из следующих утверждений верны?
1) Все высоты равностороннего треугольника равны.
2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
3) В любой ромб можно вписать окружность.
Если утверждений несколько, запишите их номера в порядке возрастания.
20. Тип 20 № 311589 
Решите уравнение:
21. Тип 21 № 311617 
Чтобы накачать в бак 117 л воды, требуется на 5 минут больше времени, чем на то, чтобы выкачать из него 96 л воды. За одну минуту можно выкачать на 3 л воды больше, чем накачать. Сколько литров воды накачивается в бак за минуту?
22. Тип 22 № 311613 
Первая прямая проходит через точки и Вторая прямая проходит через точки и Найдите координаты общей точки этих двух прямых.
23. Тип 23 № 311548 
Найдите величину угла AOE, если OE — биссектриса угла AOC, OD — биссектриса угла COB.
24. Тип 24 № 51 
В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм — прямоугольник.
25. Тип 25 № 311708 
В прямоугольном треугольнике ABC с прямым углом B, проведена биссектриса угла A. Известно, что она пересекает серединный перпендикуляр, проведенный к стороне BC в точке K. Найдите угол BCK, если известно, что угол ACB равен 40°.






























