Параллельность плоскостей

Повторим стереометрию

Аксиомы стереометрии:

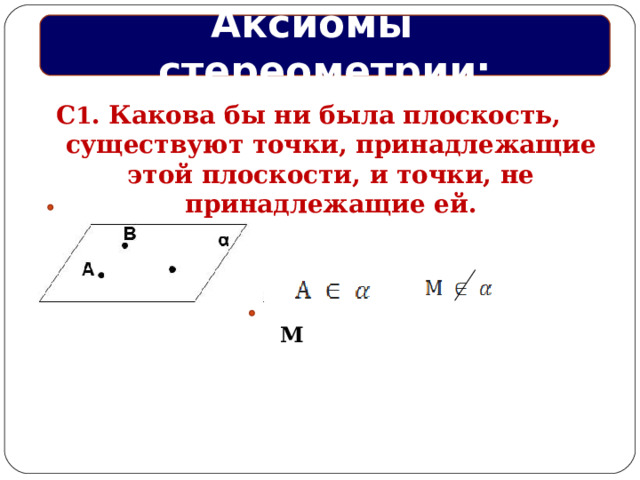
С 1 . Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.

М

Аксиомы стереометрии:

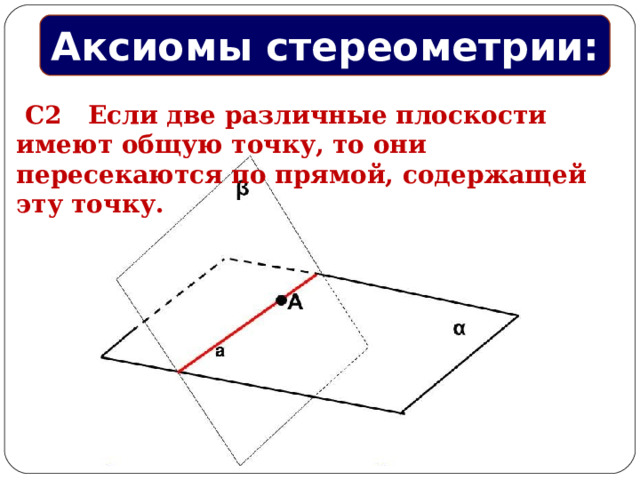
С2 Если две различные плоскости имеют общую точку, то они пересекаются по прямой, содержащей эту точку.

Аксиомы стереометрии:

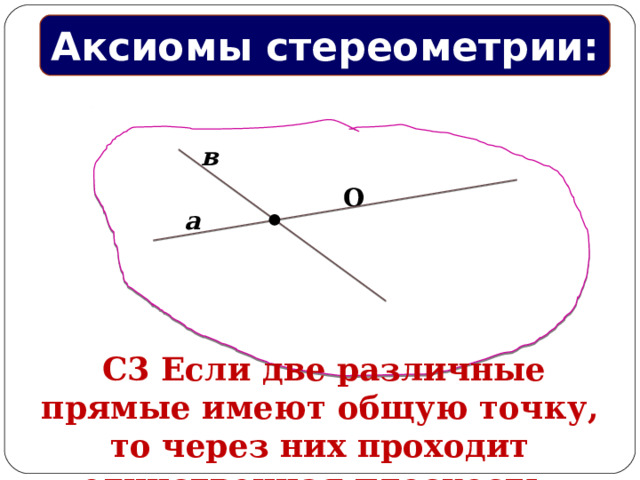
в

а

О

С3 Если две различные прямые имеют общую точку, то через них проходит единственная плоскость.

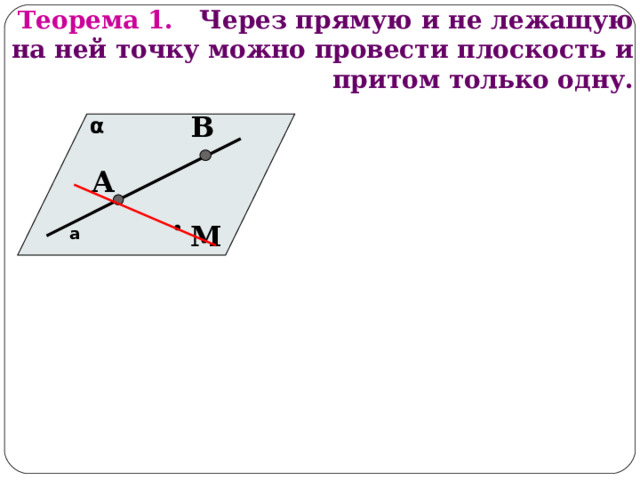
Теорема 1. Через прямую и не лежащую на ней точку можно провести плоскость и притом только одну.

В

α

А

М

а

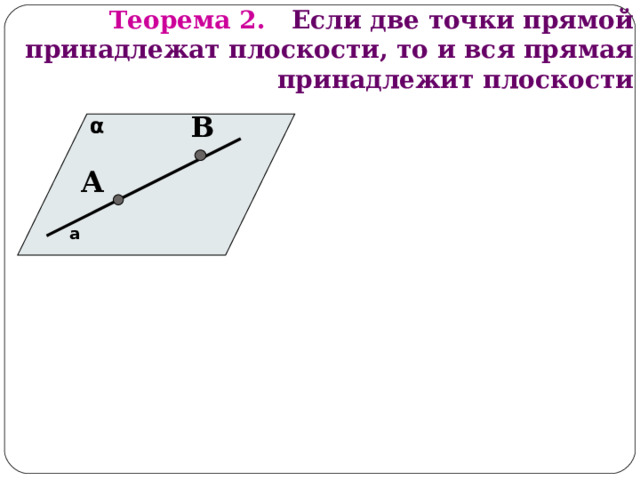
Теорема 2. Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости

В

α

А

а

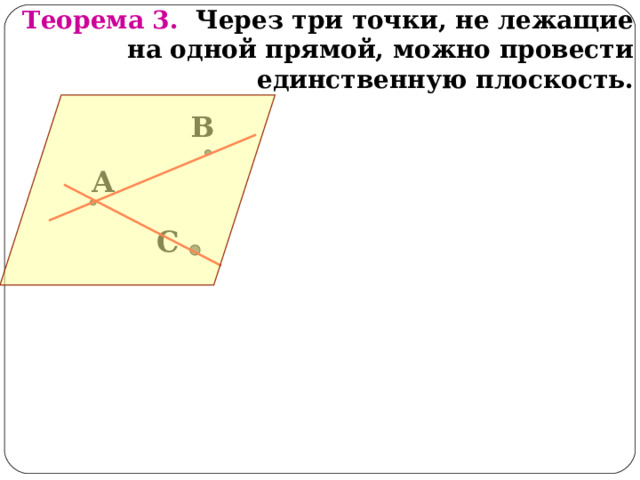
Теорема 3. Через три точки, не лежащие на одной прямой, можно провести единственную плоскость.

В

А

С

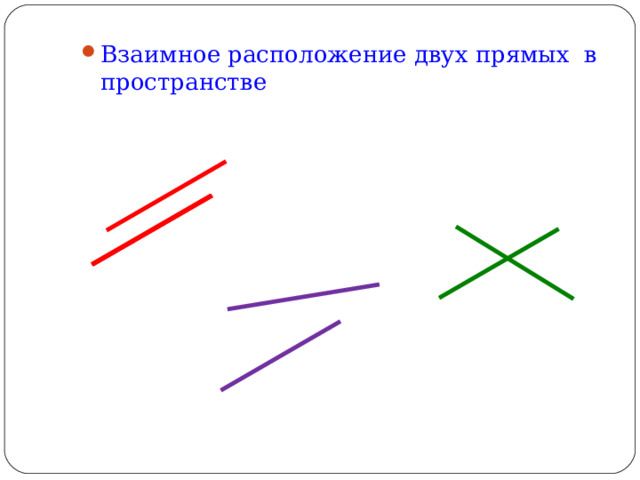
• Взаимное расположение двух прямых в пространстве

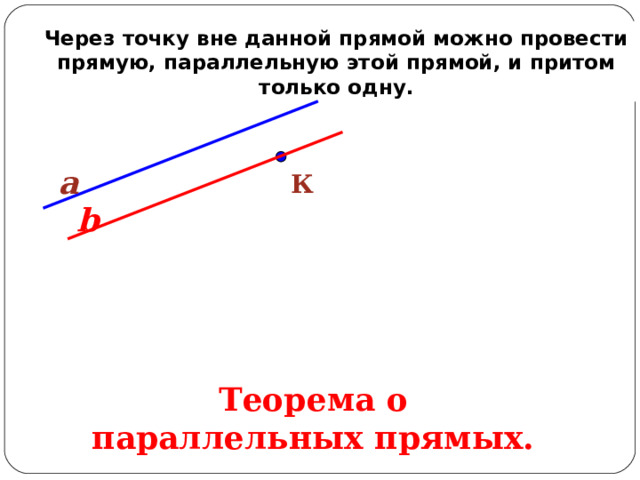
Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну.

a

К

b

Теорема о параллельных прямых.

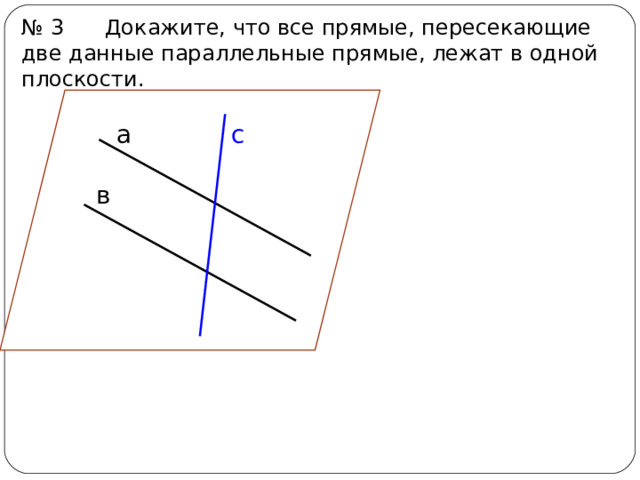
№ 3 Докажите, что все прямые, пересекающие две данные параллельные прямые, лежат в одной плоскости.

а

с

в

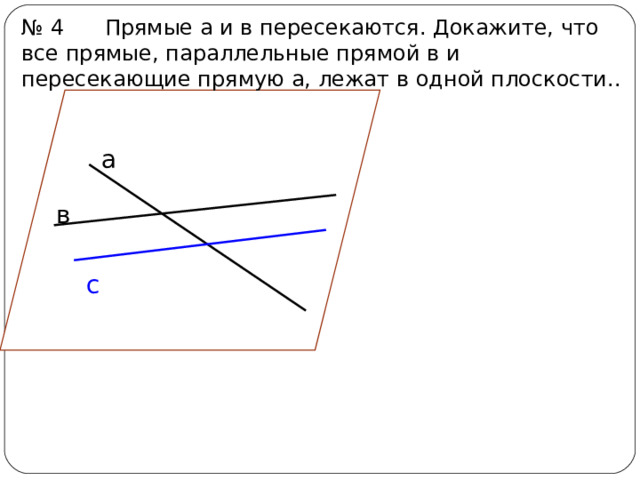
№ 4 Прямые а и в пересекаются. Докажите, что все прямые, параллельные прямой в и пересекающие прямую а, лежат в одной плоскости..

а

в

с

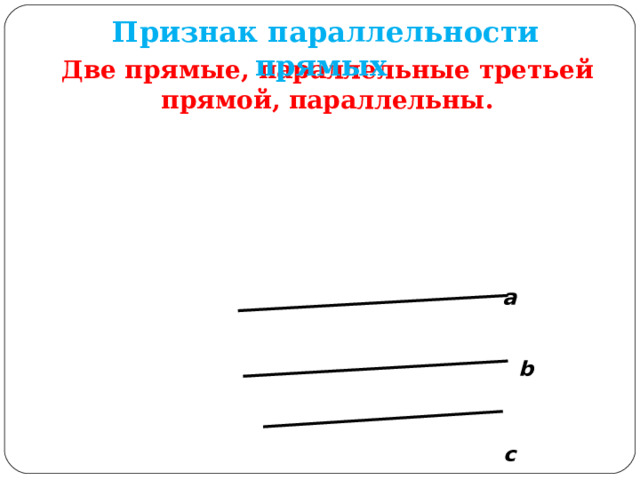
Признак параллельности прямых

Две прямые, параллельные третьей прямой, параллельны.

a

b

c

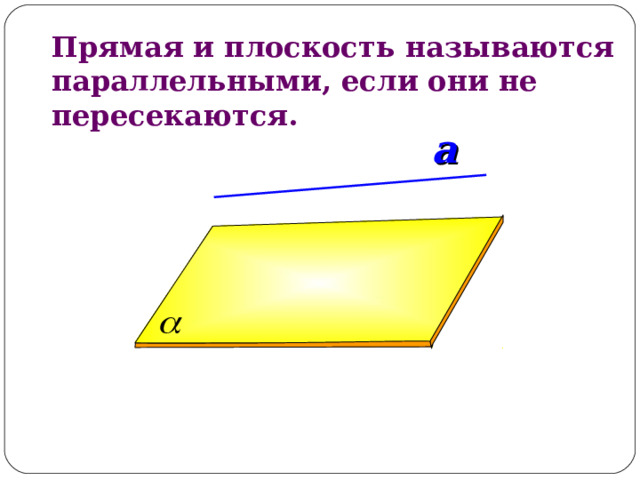
Прямая и плоскость называются параллельными, если они не пересекаются.

a

13

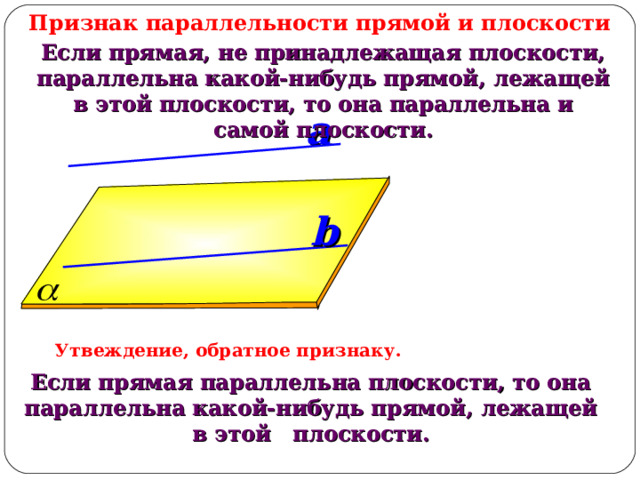
Признак параллельности прямой и плоскости

Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна и самой плоскости.

a

b

Утвеждение, обратное признаку.

Если прямая параллельна плоскости, то она параллельна какой-нибудь прямой, лежащей в этой плоскости.

13

Взаимное расположение плоскостей

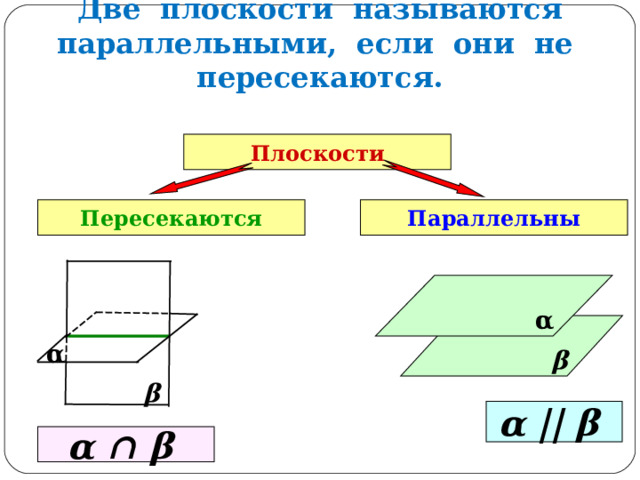
Две плоскости называются параллельными, если они не пересекаются.

Плоскости

Пересекаются

Параллельны

α

α

β

β

α || β

α ∩ β

Параллельность плоскостей

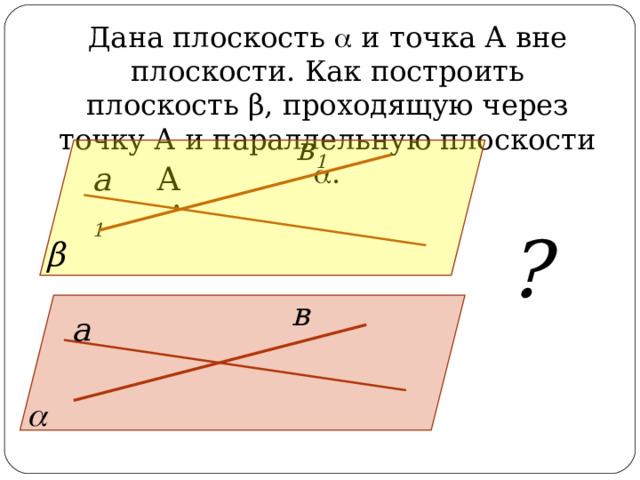
Дана плоскость  и точка А вне плоскости. Как построить плоскость β , проходящую через точку А и параллельную плоскости  .

в 1

А

а 1

?

β

в

а



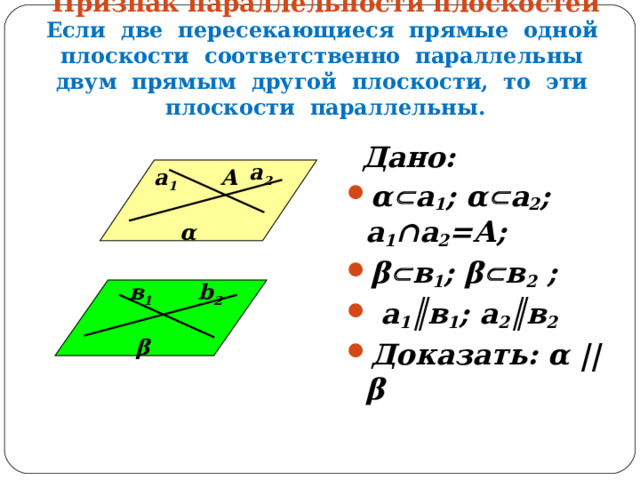
Признак параллельности плоскостей Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Дано:

• α  а 1 ; α  а 2 ; а 1 ∩а 2 =А;
• β  в 1 ; β  в 2 ;
• а 1 ║в 1 ; а 2 ║в 2
• Доказать: α || β

а 2

а 1

А

α

b 2

в 1

β

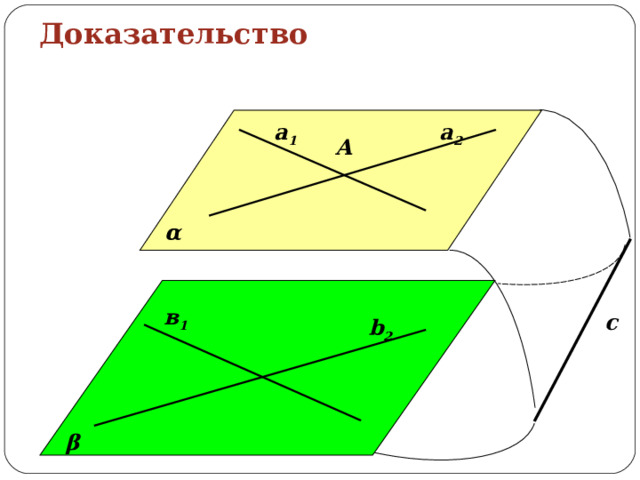
Доказательство

а 1

а 2

А

α

в 1

с

b 2

β

Доказательство от противного

а 2

а 1

Предположим α ∩ β = с

А

α

а 1 ║в 1  а 1 ║β  а 1 ∩ β

с

b 2

b 1

а 2 ║в 2  а 2 ║β  а 2 ∩ β

β

 а 1 ∩с, а 2 ∩с(с∈ β )

 а 1 ║ с, а 2 ║ с

 В плоскости  через точку А проходят две прямые а 1 и а 2 , параллельные прямой с,

что противоречит аксиоме параллельных.

Предположение α ∩ β = с - неверно  α || β

Доказать, что через две скрещивающиеся прямые можно провести параллельные плоскости.

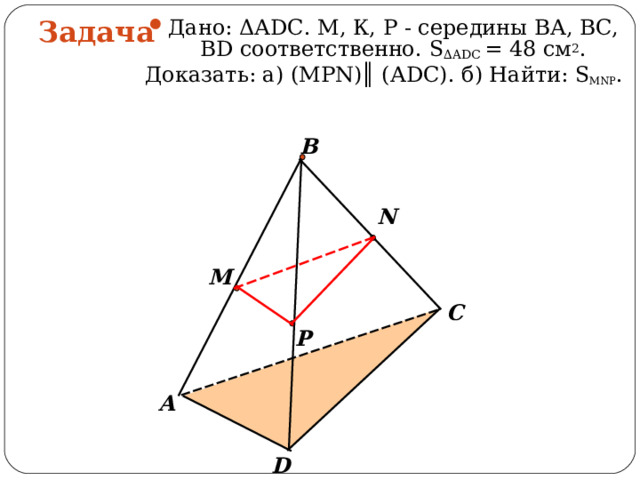
• Дано: ΔА D С. М, К, Р - середины ВА, ВС, В D соответственно. S ∆ADC = 48 см 2 .

Доказать: а) (МР N )║ (А D С). б) Найти: S MNP .

Задача

В

N

М

C

Р

А

D

Домашнее задание

• Признак параллельности плоскостей наизусть, № 19