Конспект урока.
Предмет: геометрия
Класс: 10а
УМК: Геометрия. 10-11 классы: учеб. для учащихся общеобразоват. учреждений : базовый и профил. уровни / [Л. С. Атанасян, В. Ф.Бутузов, С.Б. Кадомцев и др.]. – 22-е изд.,стер. – М. : Просвещение, 2013. – 255 с. : ил. – (МГУ – школе).
Тема урока: Параллельные прямые в пространстве. Параллельность трёх прямых
Цели урока:
-
Рассмотреть взаимное расположение прямых в пространстве. Ввести понятие параллельных прямых.
-
Доказать теоремы о параллельности прямых и параллельности 3-х прямых в пространстве.
-
Закрепить данные понятия.
Тип урока: изучение нового материала
План урока:
-
Организационный момент
-
Актуализация опорных знаний
-
Изучение нового материала
-
Первичное закрепление.
-
Домашнее задание.
-
Итог. Рефлексия.
Необходимое оборудование: тестовые задания, карточки для рефлексии.
Ход урока
1. Организационный момент.
Проверка д/з. Сообщение темы и цели урока (учитель объявляет тему урока, ставлю цель урока, отмечаю отсутствующих, учащиеся записывают в тетрадь число и тему урока).
Сообщение из истории параллельных прямых и их применения (учитель говорит вступительное слово к теме урока).
Геометрия, которую мы изучаем, называется евклидовой, по имени древнегреческого ученого Евклида (3 век до нашей эры), создавшего замечательное руководство по математике под названием «Начала». В этой книге есть раздел о параллельных прямых. В советском энциклопедическом словаре слово « параллельность» переводится с греческого языка как «идущий рядом».
В средние века параллельность обозначалась знаком «=». В 1557 году Р. Рекордом для обозначения равенства был введен знак «=», которым мы пользуемся сейчас, а параллельность стали обозначать «║».
В книге «Начала» определение параллельных прямых звучало так «прямые, лежащие в одной плоскости и будучи бесконечно продолжены в обе стороны, ни с той, ни с другой стороны не пересекаются». Это определение почти не отличается от современного.
В области параллельных прямых работало очень много учёных: Н.И. Лобаческий (18-19 век); Аббас ал-Джаухари (работал в Багдаде в 9веке); Фадл ал-Найризи (Богдад 10 век); Герард (Италия 12 век); Иоганн Генрих Ламберт (Берлин) и многие другие.
2. Актуализация опорных знаний.
Учащимся задаются вопросы.
1) Определение параллельных прямых (две прямые на плоскости называются параллельными, если они не пересекаются);
2) Взаимное расположение 2-х прямых на плоскости (2 прямые на плоскости либо пересекаются, либо параллельны);
3) Как через точку А, заданную вне данной прямой а, провести прямую, параллельную а?
4) Сколько таких параллельных (к прямой а через точку А) можно провести? Почему? (только одну, по аксиоме о параллельных прямых);
5) Аксиома параллельных (через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной).
3. Изучение нового материала
1) Каково расположение 2-х прямых на плоскости (рис. 1 а, б, в) (учащиеся работают устно: 2 прямые могут совпадать, пересекаться или быть параллельны).
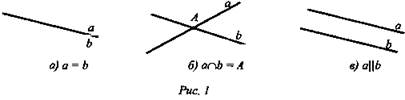
2) Перейдем к взаимному расположению 2-х прямых в пространстве. Как и в планиметрии, две различные прямые в пространстве либо пересекаются в одной точке, либо не пересекаются (не имеют общих точек). Однако второй случай допускает две возможности: прямые лежат в одной плоскости или прямые не лежат в одной плоскости. Сегодня мы рассмотрим прямые, которые лежат в одной плоскости, их называют параллельными прямыми.
Определение: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются (учащиеся записывают определение в тетрадь)
3) Докажем теорему о параллельных прямых (учащиеся читают теорему, учитель спрашивает, что дано и что будем доказывать; учитель работает с доской, изображает рисунок и записывает доказательство; учащиеся фиксируют в тетради формулировку теоремы, рисунок и доказательство теоремы)
Теорема: Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
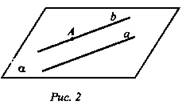
 Дано:, А, А ∈ а.
Дано:, А, А ∈ а.
Доказать: а || b, b – единственная.
Доказательство:
Откроем учебники на странице 10 и обратимся к рисунку 12. В дальнейшем нам понадобятся такие понятия: два отрезка называются параллельными, если они лежат на параллельных прямых (CD || EF), аналогично определяются параллельность отрезка и прямой (AB||a, параллельность двух лучей (CD || EF).
Докажем лемму о пересечении плоскости параллельными прямыми, которой будем пользоваться в дальнейшем (учащиеся читают лемму, учитель спрашивает, что дано и что будем доказывать; учитель работает с доской, изображает рисунок и записывает доказательство; учащиеся фиксируют в тетради формулировку леммы, рисунок и доказательство леммы).
Лемма: Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
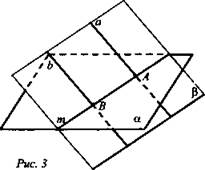 Дано: а || b, α, а ∩ α = А.
Дано: а || b, α, а ∩ α = А.
Доказать: b ∩ α.
Доказательство:
4) Из планиметрии известно: Если две прямые параллельны третьей прямой, то они параллельны. Аналогичное утверждение имеет место и для 3-х прямых в пространстве.
Теорема: Если 2 прямые параллельны третьей прямой, то они параллельны.
Дано: а || с; b || с (рис. 4).
Доказать, что а || b, то есть 1) лежат в одной плоскости; 2) не пересекаются.
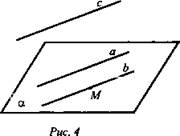
Доказательство:
4. Первичное закрепление.
Посмотрим, насколько вы усвоили новый материал. Открываем учебник на странице 31, читаем вопросы №1,№2,№3(учащиеся читают вопросы, учитель спрашивает кого-нибудь из учащихся).
№1. Верно ли утверждение: если 2 прямые не имеют общих точек, то они параллельны?(да, верно)
№2. Точка М не лежит на прямой а. Сколько прямых, не пересекающих прямую а, проходит через точку М? (одна, как на плоскости, так и в пространстве) Сколько из этих прямых параллельны а? (одна)
№3. Прямые а и с параллельны, а прямые a и b пересекаются. Могут ли прямые b и c параллельными? (нет, по Т2 : 2 прямые параллельны третьей прямой, параллельны)
5. Домашнее задание
Записываем домашнее задание. Пункт 4, 5, теоремы, задача №16 стр.13 (учитель диктует домашнее задание, учащиеся записывают в дневник).
Задача № 16
Дано: 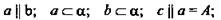
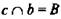 (рис. 6).
(рис. 6).
Доказать: с ⊂ α.
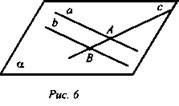
Доказательство: По условию а ∩ с = А; b ∩ с = В, значит А ∈ α и В ∈ α, так как а ⊂ α иb ⊂ α, по А2 с ⊂ α, что и требовалось доказать.









 Дано:, А, А ∈ а.
Дано:, А, А ∈ а.  Дано: а || b, α, а ∩ α = А.
Дано: а || b, α, а ∩ α = А.



















