Инструкционная карта №
Тақырыбы/ Тема: «Первообразная».
Мақсаты/ Цель:
1.Обеспечить усвоение учащимися умения применять формулы первообразных, три правила вычисления первообразной и основное свойство первообразных при решении упражнений и заданий.
2. При решении упражнений, развивать у учащихся умения выделять главное, существенное в изучаемом материале, обучить умению рационально находить правильное решение изучаемого вопроса.
3. Создать условие для развития коммутативно-творческих умений: не шаблонно подходить решению разнообразных задач.
Теоретический материал:
Таблица первообразной.
|
Функция ƒ | k (посто-янная) | xn (n Z, Z, n -1) -1) | 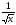
|
sin x |
cos x | 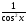
| 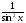
|
| Общий вид первообраз- ных для ƒ |
kx+C | 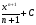
|
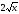 +C +C
|
-cos x+C |
sin x+C |
tg x+C |
-ctg x+C |
Основное свойство первообразных: Любая первообразная для функции ƒ на промежутке I может быть записана в виде F(x)+C , где F(x)- одна из первообразных для функции ƒ(x) на промежутке I, а C-произвольная постоянная.
Пример: Найти общий вид первообразных для функции ƒ(x)=-x3 на R. F(x)=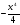 +C.
+C.
Правило 1. Если F есть первообразная ƒ, а G- первообразная для g, то F+G есть первообразная для ƒ+g (первообразная двух функций равна сумме их первообразных).
Приём нахождения первообразных суммы двух функций
Представьте заданную функцию как сумму двух функций.
Найдите первообразную первой функции.
Найдите первообразную второй функции.
Запишите сумму найденных первообразных.
Пример: Найти общий вид первообразных для функции ƒ:
ƒ(x)=sin x+cos x F(x)=-cos x+sin x+C
Правило 2.Если F есть первообразная для функции ƒ, а k-постоянная, то kF есть первообразная для функции kƒ.
Приём нахождения первообразной функции kƒ
Представьте заданную функцию в виде произведения двух множителей, один из них которых- число, другой- не которая функция.
Запишите первообразную найденной функции.
Умножьте полученную на выделенный числовой множитель.
Пример: Найти общий вид первообразных для функции ƒ:
ƒ(x)=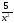 -5x+7 F(x)=-
-5x+7 F(x)=-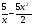 +7x+C
+7x+C
Правило 3.Если F(x) есть первообразная для функции ƒ(x), а k и b- постоянные, причем k 0, то
0, то 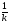 F(kx+b) есть первообразная для функции ƒ(kx+b).
F(kx+b) есть первообразная для функции ƒ(kx+b).
Приём нахождения первообразной функции ƒ(kx+b)
Представьте заданную сложную функцию как композицию двух функций, где «внутренняя» функция - линейная.
Запишите формулу, заданную «внешнюю» функцию.
Найдите первообразную «внешней» функции.
Запишите формулу, заданную первообразную сложной функции, составьте произведения числа 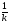 и первообразной «внешней» функции с аргументом kx+b.
и первообразной «внешней» функции с аргументом kx+b.
Пример: Найти общий вид первообразных для функции ƒ:
1) ƒ(x)= , F(x)=
, F(x)=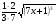 +C=
+C=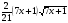 +C
+C
2) ƒ(x)=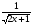 -sin
-sin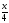 , F(x)=
, F(x)=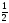 ∙2
∙2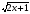 +4sin
+4sin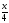 +C=
+C=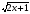 +4sin
+4sin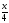 +C
+C
Практическая часть:
| 1 вариант Найдите первообразную функции: | 2 вариант Найдите первообразную функции: | 3 вариант Найдите первообразную функции: | 4 вариант Найдите первообразную функции: |
| ƒ(x)=4x2+13x4; | ƒ(x)=-2x2-12x3; | ƒ(x)=x4+2,5x2; | ƒ(x)=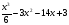 ; ; |
| ƒ(x)=3x-sinx; | ƒ(x)=cosx-1; | ƒ(x) =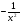 +sinx; +sinx; | ƒ(x)=6x-sinх; |
| ƒ(x)=cosx+4; | ƒ(x)=3sinx-x; | ƒ(x) = ; ; | ƒ(x)=cos2x-sin2x; |
| Найдите общий вид первообразных F(x) для функции: |
| ƒ(x) = на промежутке (0,5; ∞); на промежутке (0,5; ∞); | ƒ(x) = ; ; | ƒ(x)= ; ; | ƒ(x)= ; ; |
| ƒ(x) = - sin2x; - sin2x; | ƒ(x) = - cos3x; - cos3x; | ƒ(x)= на промежутке (-0,5; ∞); на промежутке (-0,5; ∞); | ƒ(x)= ; ; |
| ƒ(x)=sin(1,5x-1)+ ; ; | ƒ (x)= ; ; | g(x)= ; ; | ƒ(x)= + +  |
| Для функции ƒ(x)=sin x+1 найдите первообразную, график которой проходит через точку М (0; -3). | Для функции ƒ(x)=3x2+2x найдите первообразную, принимающую значение, равное 81 при x=1. | Для функции ƒ(x)=sin x найдите первообразную F(x), график которой проходит через точку А . . | Для функции ƒ(x)=-x+1 найдите первообразную, график которой проходит через точку М (-2; -3). |
Контрольные вопросы:
Что называется первообразной для данной функции?
Какая форма связи имеется между понятиями производная и первообразная?
Сформулируйте три правила вычисления первообразной.







 Z,
Z, -1)
-1)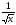
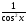
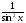
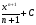
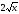 +C
+C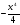 +C.
+C. 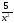 -5x+7 F(x)=-
-5x+7 F(x)=-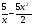 +7x+C
+7x+C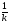 F(kx+b) есть первообразная для функции ƒ(kx+b).
F(kx+b) есть первообразная для функции ƒ(kx+b). , F(x)=
, F(x)=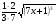 +C=
+C=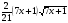 +C
+C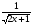 -sin
-sin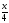 , F(x)=
, F(x)=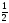 ∙2
∙2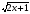 +4sin
+4sin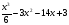 ;
; 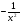 +sinx;
+sinx; 


















