Конспект урока
Учебник: Мордкович. 11 класс. В 2 ч. Ч 1. Учебник для учащихся общеобразовательных учреждений/ А. Г. Мордкович, П. В. Семенов. – 12-е изд., стер. – М. : Мнемозина, 2010 – 224 с. Глава 3. §11.
Тема урока: Показательная функция, её свойства и график.
Тип урока: урок освоения теории
Учебная задача урока: провести усвоение теоретического материала по теме «Показательная функция её свойства и график»
Диагностируемые цели урока:
Знает:
Определение степени с действительным показателем
Определение предела
понятие показательной функции, её свойства и вид графика;
2.Умеет:
Находить значения выражений, используя свойства степеней
строить график показательной функции;
перечислять свойства показательной функции;
решать простейшие показательные уравнения и неравенства;
3.Понимает:
что степени с любыми действительными показателями обладают всем привычными свойствами степеней
что вид графика показательной функции зависит от её основания;
что решение простейших показательных уравнений и неравенств основано на теоремах о показательных равенствах и неравенствах
Планируемые результаты (УУД):
Личностные: умение учащегося устанавливать связи между целью учебной деятельности и ее мотивом, т.е. между результатом учения, и тем, что побуждает деятельность, ради чего она осуществляется, таким образом должна осуществляться осмысленная организация собственной деятельности ученика.
Регулятивные: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что еще неизвестно, планирование – определение последовательности промежуточных целей с учетом конечного результата, оценка – выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками, т.е. определение цели сотрудничества, функций учеников, способов взаимодействия, умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка, умение доказывать собственное мнение.
Познавательные: анализ объектов с целью выделения признаков (существенных, несущественных); выдвижение гипотез и их обоснование; построение логической цепи рассуждений, доказательство; подведение под понятие; выведение следствий; установление причинно-следственных связей.
Методы обучения: репродуктивный, частично-поисковые, УДЕ.
Форма работы: фронтальная, индивидуальная.
Средства обучения: традиционные, презентация, карточки с заданиями для самостоятельной работы.
Структура урока:
1) Мотивационно–ориентировочная часть (10 минут).
2) Операционно-познавательная часть (20 минут).
3) Рефлексивно-оценочная часть (15 минут).
Предваряющее домашнее задание:
Построить график функции и перечислить её свойства: а) 𝑦=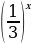 б) 𝑦=
б) 𝑦=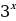
Ход урока
Мотивационно–ориентировочная часть.
Актуализация
Задание 1. Какие из представленных функций являются показательными?
А) 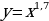
Б) 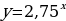
В) 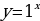
Г) 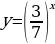
Ответ: Б, Г
-Сформулируйте определение показательной функции.
-Функцию вида y=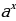 , где
, где 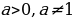 называют показательной функцией
называют показательной функцией
Проверка домашнего задания
Построить график функции и перечислить её свойства: а) 𝑦=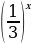 б) 𝑦=
б) 𝑦=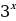
Решение:
а) 𝑦=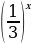

Свойства:
D(f)=(-∞; +∞);
Не является ни четной и ни нечетной;
Убывает;
Не ограничена сверху, ограничена снизу;
Не имеет ни наибольшего, ни наименьшего значений;
Непрерывна;
E(f)=(0; +∞);
Выпукла вниз.
б) 𝑦=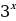

Свойства:
D(f)=(-∞; +∞);
Не является ни четной и ни нечетной;
Возрастает;
Не ограничена сверху, ограничена снизу;
Не имеет ни наибольшего, ни наименьшего значений;
Непрерывна;
E(f)=(0; +∞);
Выпукла вниз.
Мотивация
На прошлом уроке вы изучили понятие иррациональной и действительной степени и ее свойства, определение показательной функции, её свойства и вид графика, теоремы о показательных равенствах и неравенствах . В конце данного урока будет проведена самостоятельная работа по проверке изученной вами материала.
Постановка учебной задачи:
Провести усвоение теоретического материал по теме «Показательная функция, ее свойства и график»
Операционно-познавательная часть
Найдите значение выражения:
А) 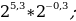
Б) 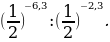
в) 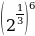
Г) 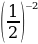
Д) 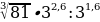
Решение:
А) 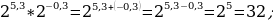
Б) 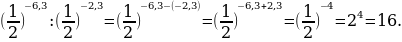
в) 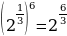 =
=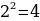
Г) 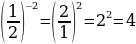
Д) 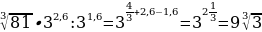
Схематично изобразите график функции:
а) 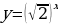
б) 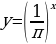
Решение:
а)

б)

Постройте график функции 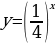 и найдите:
и найдите:
а) её значение при х= 0,5; х=3,5;
б) при каком х у= 2; у= 0,4.
Решение:

а)
1. при х= 0,5, 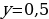
2. при х=2, 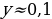
б)
1) при 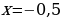 у= 2,
у= 2,
2) при 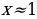 y=0,4.
y=0,4.
Постройте график функции 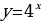 и найдите:
и найдите:
а) её значение при х= 0,5; х=-0,6;
б) при каком х у= 0,5; у= 3.
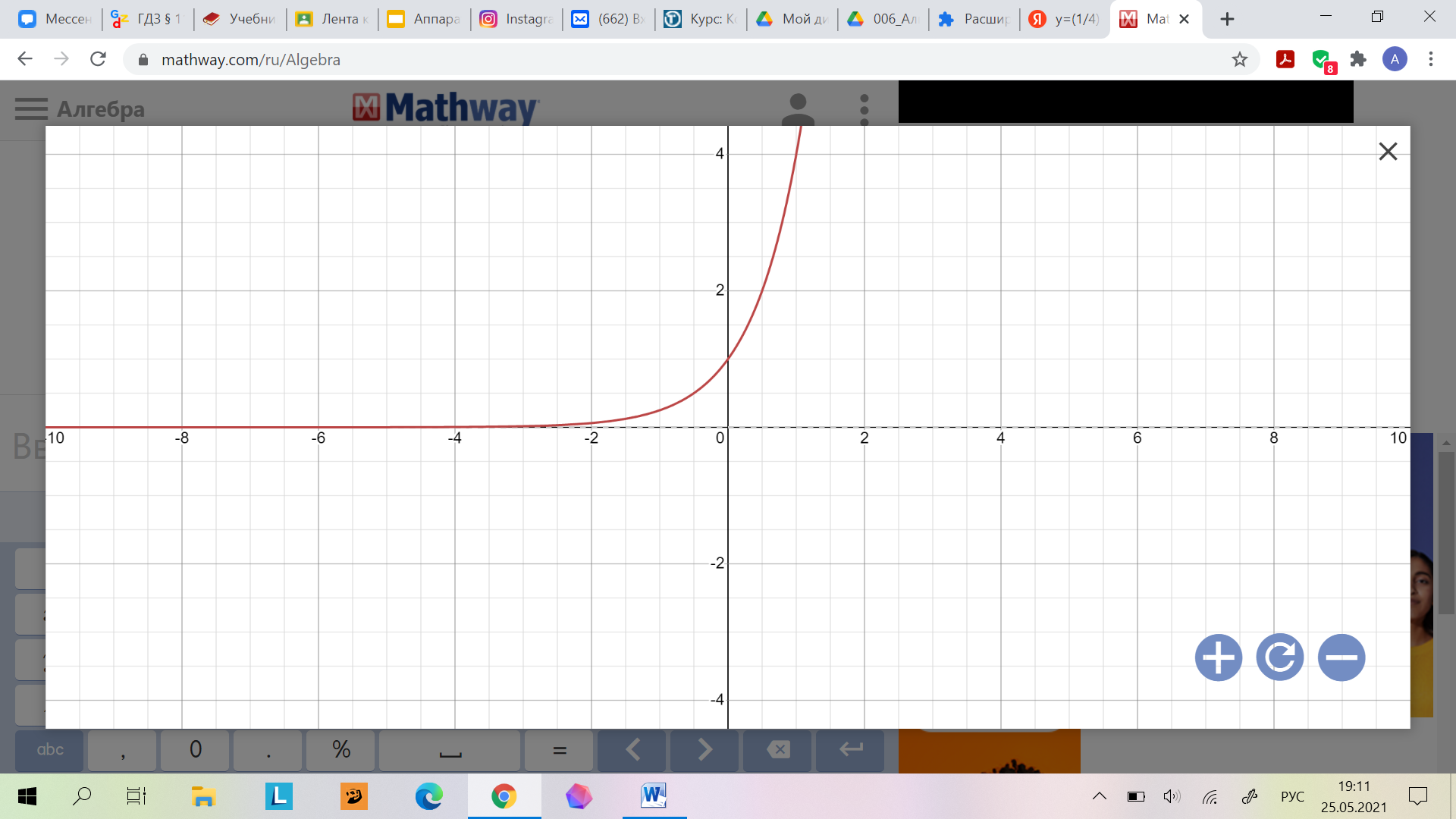
Решение:
а)
1) при х= 0,5 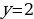
2) при х=1, y=4
б)
1) при 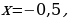 у= 0,5
у= 0,5
2) при 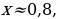 у= 3
у= 3
5. Сравните значения 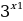 и
и 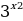 , если:
, если:
а) 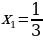 ,
, 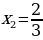
б) 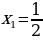 ,
, 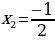
Решение:
а) Т.к. 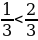 и 31, функция
и 31, функция 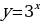 возрастает, то
возрастает, то 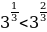
б) Т.к. 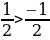 и 31, функция
и 31, функция 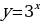 возрастает, то
возрастает, то 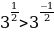
6. Сравните значения 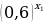 и
и 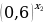 , если:
, если:
а) х1=0,2 , х2= 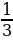 ;
;
б) x1=-4,1; х2=-5.
Решение:
а) Т.к. 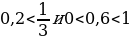 , функция
, функция 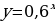 убывает, то
убывает, то 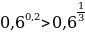
б) Т.к. 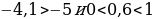 , функция
, функция 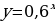 убывает, то
убывает, то 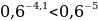
7. Найдите наибольшее и наименьшее значения заданной функции на заданном промежутке:
А) 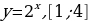 ;
;
Б) 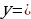 .
.
Решение:
А) 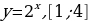 ;
;
Т.к. 21, то функция 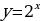 возрастает на всей области определения
возрастает на всей области определения
yнаим=y(2)=21=2; yнаиб=y(4)=24=16.
Б) 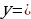
Т.к. 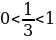 , то функция
, то функция 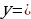 убывает на всей области определения
убывает на всей области определения
yнаим=y(-2)=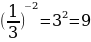 ; yнаиб= y(-4)=
; yнаиб= y(-4)=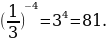
9.Решите уравнение (неравенство):
А)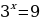 ;
;
Б) 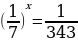
В)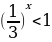 ;
;
Г)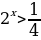 .
.
Решение:
А) 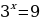 ;
;
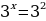 ;
;
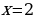 ;
;
Ответ: 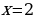 .
.
Б) 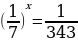 ;
;
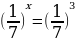 ;
;
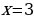 .
.
Ответ: 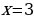 .
.
В)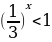 ;
;
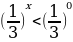 ;
;
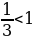
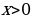 .
.
Ответ: 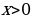 .
.
Г)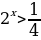 ;
;
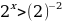 ;
;
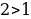
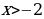
Ответ: 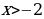
Рефлексивно-оценочная часть
| Какова была цель урока? | Провести усвоение теоретического материал по теме «Показательная функция, ее свойства и график»
|
| Достигли ли мы ее? | Нет, т.к. не написана самостоятельная работа. |
| Как достигли? | Решали задачи на свойства степеней, чтение графика функции, нахождение наибольшего и наименьшего значений функций, решение простейших уравнений и неравенств, сравнение чисел с действительными и иррациональными показателями. |
Домашнее задание:
№11.2 (а, б), №11.3 (в, б), №11.5 (а, б), №11.13 (в, г), №11.20 (б, г), №11.23 (а), №11.33 (в, г), №11.59 (б, в), №11.67(б, в)
Решение домашнего задания.
№11.2 (а, б)
А) 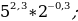
Б) 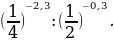
Решение:
А) 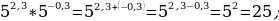
Б) 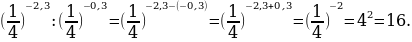
№11.3 (в, б)
в) 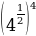
Г) 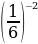
Решение:
в) 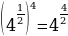 =
=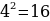
Г) 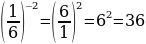
№11.5 (а, б)
А)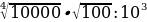
Б)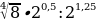
Решение:
А) 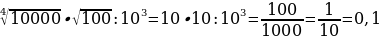
Б) 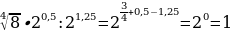
№11.13 (в, г). Схематично изобразите график показательной функции:
В) 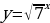 ;
;

Г) 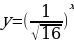

№11.20. Сравните значения 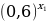 и
и 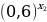 , если:
, если:
б)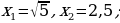
г) 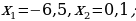
Решение:
б) Т.к. 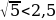 и
и 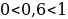 , функция
, функция 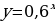 убывает, то
убывает, то 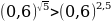
г) Т.к.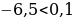 и
и 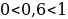 , функция
, функция 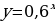 убывает, то
убывает, то 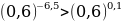
№11.23. Расположите числа в порядке возрастания:
А) 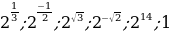 .
.
Решение:
А)Т.к. 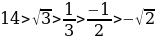 , 21, функция
, 21, функция 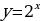 - возрастает, то
- возрастает, то 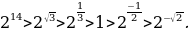
Ответ: 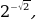
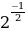 , 1,
, 1, 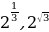 ,
, 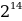
№11.33 (в, г). Найдите наибольшее и наименьшее значения заданной функции на заданном промежутке:
в) 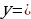
Т.к. 0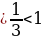 , то функция
, то функция 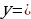 убывает на всей области определения
убывает на всей области определения
yнаим=y(4)=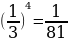 ; yнаиб= y(0)=
; yнаиб= y(0)=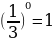 .
.
г) 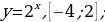
Т.к.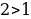 , то функция
, то функция 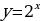 возрастает на всех области определения
возрастает на всех области определения
yнаим=y(-4)=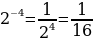 ; yнаиб= y(2)=
; yнаиб= y(2)=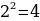 .
.
№11.59(б, г)
Б) 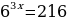 ;
;
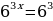 ;
;
3х = 3
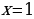 ;
;
Ответ: 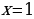 .
.
В) 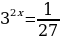 ;
;
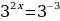 ;
;
2х = -3
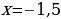 .
.
Ответ: 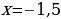 .
.
№11.67(б,в)
Б)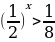 ;
;
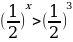 ;
;
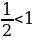
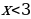 .
.
Ответ: 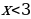 .
.
В)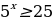 ;
;
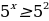 ;
;
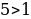
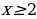
Ответ: 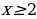
Самостоятельная работа
| 1 Вариант Перечислите свойства функции 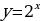 Сформулируйте теоремы №3 и № 4 В одной системе координат схематично изобразите графики функций 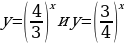 | 2 Вариант Перечислите свойства функции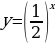  Сформулируйте теоремы №1 и №2 В одной системе координат схематично изобразите графики функций 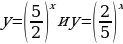 |
Решения:
Вариант
№ 1. 1.D(f): x (-∞;+∞). 2. Е(f): (0;+∞). 3. Не является ни четной, ни нечетной 4. Возрастает 5. Ограничена снизу, не ограничена сверху. 6. Не имеет ни наибольшего, ни наименьшего значений. 7. Непрерывна 8. Выпукла вниз
№ 2 Теорема 3. Если 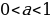 , то равенство , то равенство 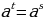 справедливо тогда и только тогда, когда справедливо тогда и только тогда, когда 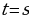 . .
Теорема 4. Если 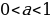 , то неравенство , то неравенство 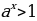 справедливо тогда и только тогда, когда справедливо тогда и только тогда, когда 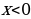 , неравенство , неравенство 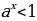 справедливо тогда и только тогда, когда справедливо тогда и только тогда, когда 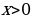 . . № 3   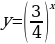
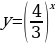
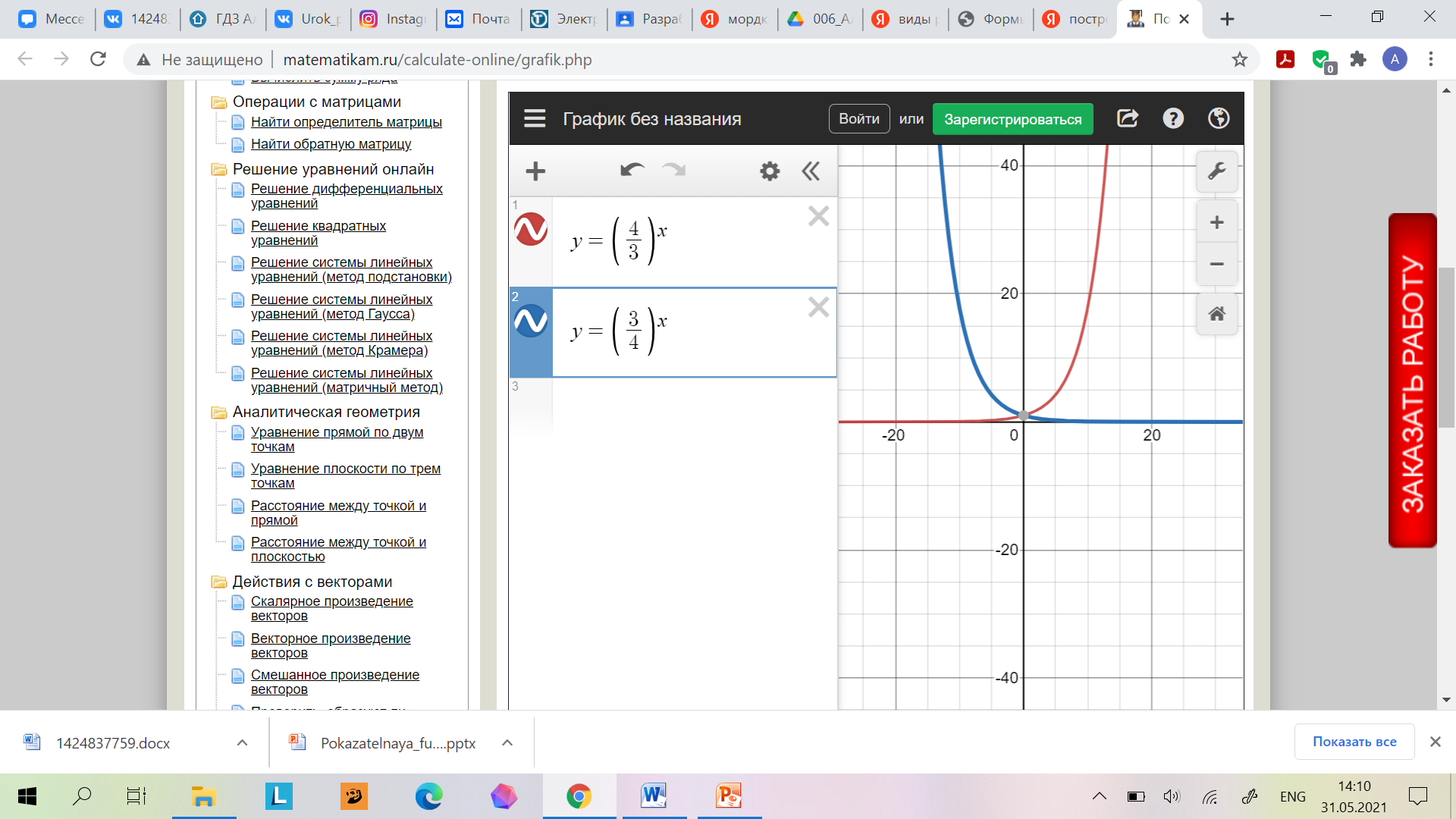 | Вариант
№ 1. 1.D(f): x (-∞;+∞). 2. Е(f): (0;+∞). 3. Не является ни четной, ни нечетной 4. Убывает 5. Ограничена снизу, не ограничена сверху. 6. Не имеет ни наибольшего, ни наименьшего значений. 7. Непрерывна 8. Выпукла вниз
№ 2 Теорема 1. Если 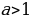 , то равенство , то равенство 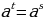 справедливо тогда и только тогда, когда справедливо тогда и только тогда, когда 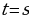 . .
Теорема 2. Если 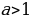 , то неравенство , то неравенство 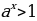 справедливо тогда и только тогда, когда справедливо тогда и только тогда, когда 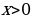 , неравенство , неравенство 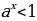 справедливо тогда и только тогда, когда справедливо тогда и только тогда, когда 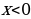 . . № 3  
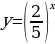
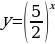
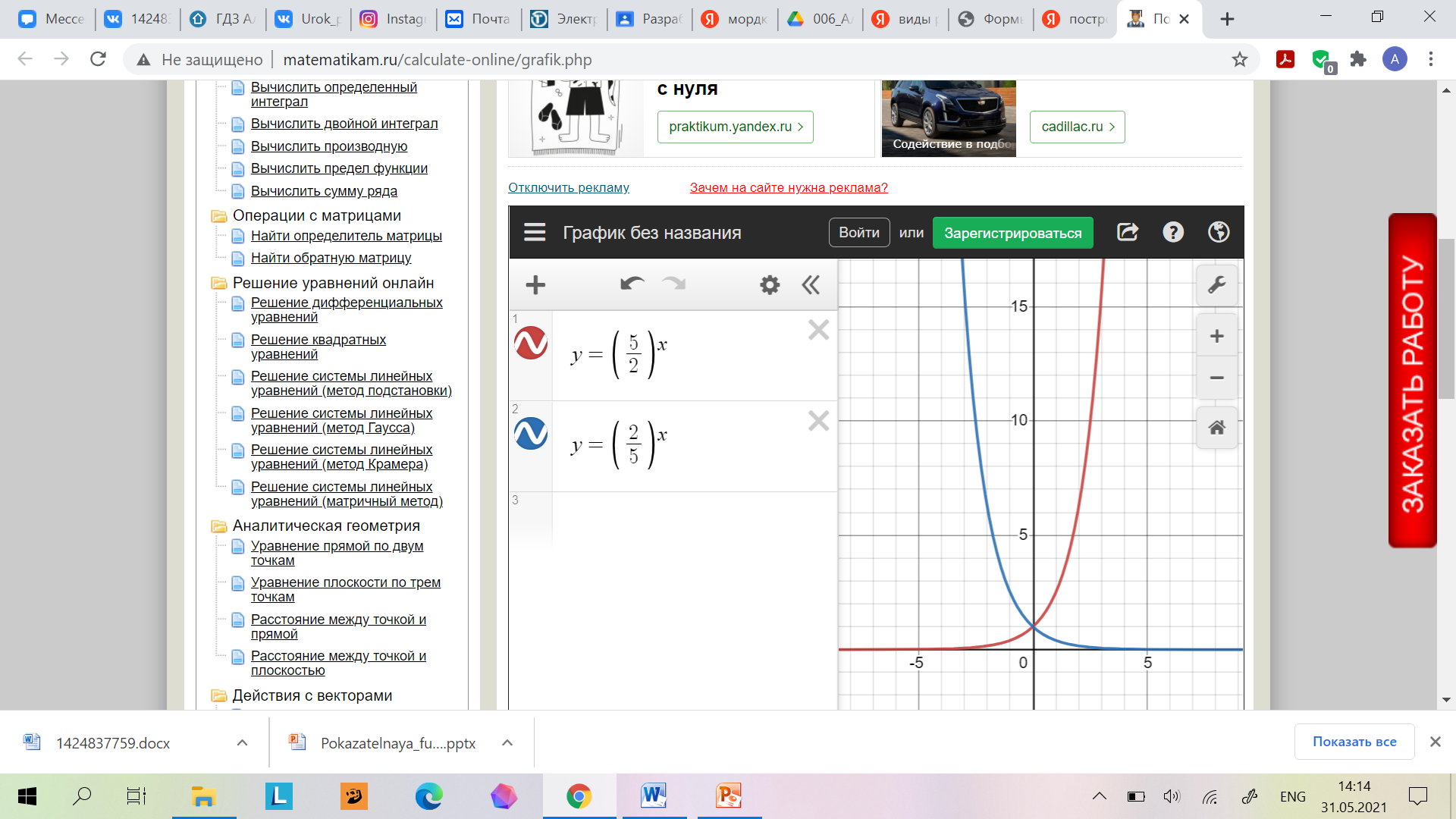 |







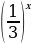 б) 𝑦=
б) 𝑦=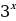
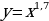
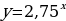
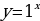
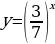
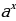 , где
, где 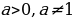 называют показательной функцией
называют показательной функцией

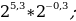
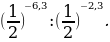
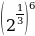
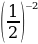
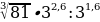
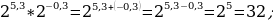
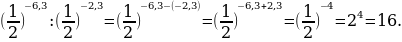
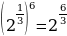 =
=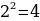
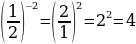
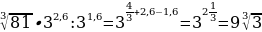
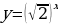
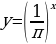


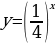 и найдите:
и найдите:
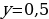
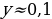
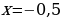 у= 2,
у= 2, 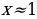 y=0,4.
y=0,4.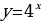 и найдите:
и найдите:
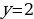
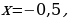 у= 0,5
у= 0,5 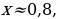 у= 3
у= 3 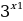 и
и 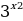 , если:
, если: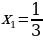 ,
, 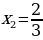
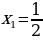 ,
, 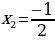
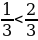 и 31, функция
и 31, функция 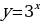 возрастает, то
возрастает, то 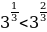
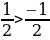 и 31, функция
и 31, функция 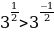
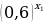 и
и 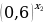 , если:
, если: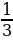 ;
;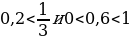 , функция
, функция 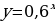 убывает, то
убывает, то 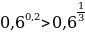
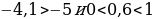 , функция
, функция 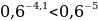
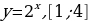 ;
;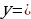 .
.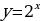 возрастает на всей области определения
возрастает на всей области определения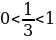 , то функция
, то функция 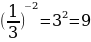 ; yнаиб= y(-4)=
; yнаиб= y(-4)=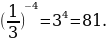
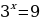 ;
;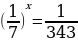
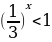 ;
;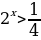 .
.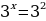 ;
;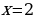 ;
;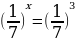 ;
;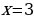 .
.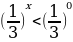 ;
;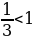
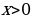 .
.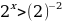 ;
;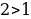
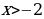
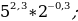
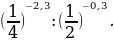
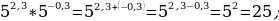
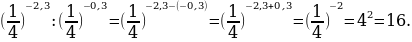
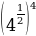
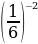
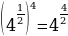 =
=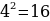
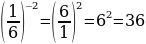
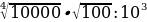
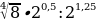
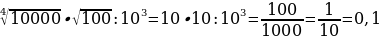
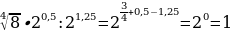
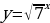 ;
;
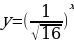

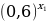 и
и 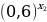 , если:
, если: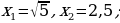
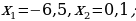
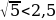 и
и 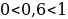 , функция
, функция 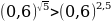
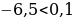 и
и 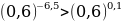
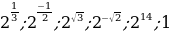 .
.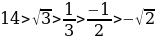 , 21, функция
, 21, функция 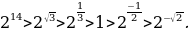
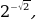
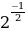 , 1,
, 1, 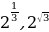 ,
, 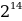
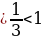 , то функция
, то функция 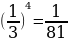 ; yнаиб= y(0)=
; yнаиб= y(0)=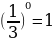 .
.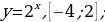
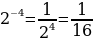 ; yнаиб= y(2)=
; yнаиб= y(2)=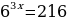 ;
;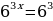 ;
;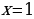 ;
;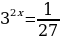 ;
;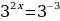 ;
;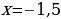 .
.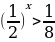 ;
;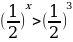 ;
;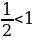
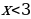 .
.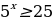 ;
;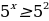 ;
;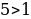
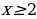
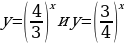
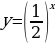

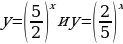
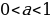 , то равенство
, то равенство 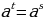 справедливо тогда и только тогда, когда
справедливо тогда и только тогда, когда 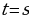 .
.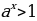 справедливо тогда и только тогда, когда
справедливо тогда и только тогда, когда 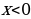 , неравенство
, неравенство 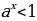 справедливо тогда и только тогда, когда
справедливо тогда и только тогда, когда 

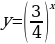
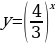

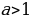 , то равенство
, то равенство