
Решение задач с помощью уравнений.
Подготовила:
учитель математики
МБОУ Г.ГОРЛОВКИ «ШКОЛА № 42
Рыбина М.В.

Алгоритм решения текстовой задачи с помощью уравнения
1) обозначить переменной одну из неизвестных величин;
2) другие неизвестные величины (если они есть) выразить через введенную переменную;
3) по условию задачи установить соотношение между неизвестными и известными значениями величин и составить уравнение;
4) решить полученное уравнение;
5) проанализировать решение уравнения и найти неизвестную величину, а при необходимости и значения остальных неизвестных величин;
6) записать ответ к задаче.

Задача 1
Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый?

Задача 1 (решение)
Пусть второй рабочий изготовил х деталей, тогда первый (х + 63) детали. Всего изготовили 657 деталей. Составляем уравнение:
х + х + 63 = 657,
2х = 657 – 63,
2х = 594,
х = 297 – деталей изготовил второй рабочий
297 + 63 = 360 (дет.) – изготовил первый рабочий
Ответ: 360 и 297 деталей

Задача 2
Три цеха за смену изготовили 599 деталей. Второй цех изготовил в два раза больше, чем первый, а третий – на 41 деталь меньше, чем второй. Сколько деталей изготовил каждый цех?

Задача 2 (решение)
Пусть первый цех изготовил х деталей, тогда второй цех - 2х деталей, а третий – (2х – 41) деталь. Всего за смену было изготовлено 599 деталей. Составляем уравнение:
х + 2х + 2х – 41 = 599,
5х = 599 + 41,
5х = 640,
х = 128 – деталей изготовил первый цех
128 2 = 256 (дет.) – изготовил второй цех
256 – 41 = 215 (дет.) – изготовил третий цех
Ответ: 128 деталей, 256 деталей, 215 деталей

Задача 3
За 9 ч по течению реки теплоход проходит тот же путь, что за 11 ч против течения. Найдите собственную скорость теплохода, если скорость течения реки 2 км/ч.
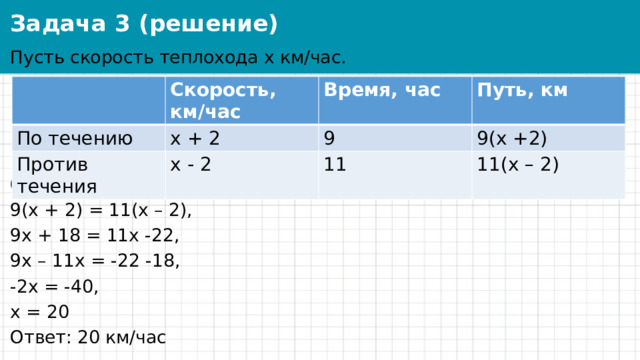
Задача 3 (решение)
Пусть скорость теплохода х км/час.
Составляем уравнение:
9(х + 2) = 11(х – 2),
9х + 18 = 11х -22,
9х – 11х = -22 -18,
-2х = -40,
х = 20
Ответ: 20 км/час
Скорость, км/час
По течению
х + 2
Время, час
Против течения
Путь, км
9
х - 2
9(х +2)
11
11(х – 2)

Задача 4
Моторная лодка плыла 4 часа по течению реки и 6 часов против течения, пройдя за это время 114 км. Найдите собственную скорость лодки, если скорость течения реки 3 км/ч.
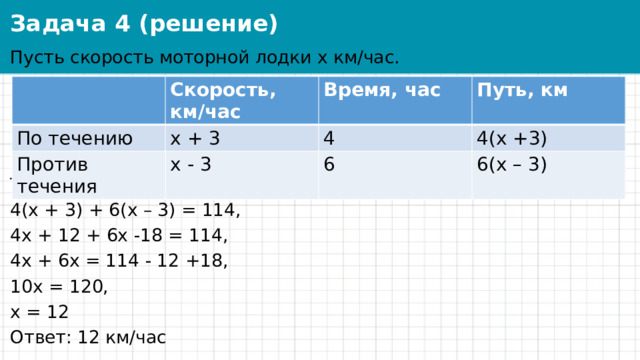
Задача 4 (решение)
Пусть скорость моторной лодки х км/час.
Так как всего пройдено 114 км, составляем уравнение:
4(х + 3) + 6(х – 3) = 114,
4х + 12 + 6х -18 = 114,
4х + 6х = 114 - 12 +18,
10х = 120,
х = 12
Ответ: 12 км/час
Скорость, км/час
По течению
х + 3
Время, час
Против течения
Путь, км
4
х - 3
4(х +3)
6
6(х – 3)

Задача 5
3а три дня турист прошёл 64 км, причём за второй день он прошел 3/7 расстояния, пройденного за первый день, а за третий – 40 % расстояния, пройденного за первый день. Сколько километров проходил турист каждый день?

Задача 5 (решение)
Пусть х км – прошел за первый день, тогда км – за второй день, а 0,4x км – за третий день. Всего пройдено 64 км. Составляем уравнение:
х + + 0,4x = 64
1 х = 35 (км) – прошел турист за первый день; 35 • = 15 (км) – прошел турист за второй день; 35 • 0,4 = 14 (км) – прошел турист за третий день. Ответ: 35 км; 15 км; 14 км.

Задача 6
В первом шкафу было в 4 раза меньше книг, чем во втором. Когда в первый шкаф поставили 17 книг, а из второго взяли 25 книг, в шкафах книг стало поровну. Сколько книг было в каждом шкафу сначала?

Задача 6 (решение)
Пусть х книг было в первом шкафу, тогда 4x книг было во втором шкафу. Когда в первый шкаф поставили 17 книг, а из второго взяли 25 книг, то книг в шкафах стало поровну. Составляем уравнение:
17 + х = 4х – 25
х – 4х = -25 – 17,
-3х = -42 х = 14 (книг) – было в первом шкафу. 4 • 14 = 56 (книг) – было во втором шкафу. Ответ: 14 книг; 56 книг.

Задача 7
Чтобы сделать вовремя заказ, артель стеклодувов должна была изготовлять в день по 40 изделий. Однако она изготовляла ежедневно на 20 изделий больше и выполнила заказ на 3 дня раньше срока. Каков был срок выполнения заказа?

Задача 7 (решение)
Пусть заказ составлял х изделий. Если бригада изготавливала бы в день по 40 деталей, то выполнила бы заказ за Но она изготавливала в день на 20 деталей больше, то есть 60, и выполнила заказ за Так как она выполнила заказ на 3 дня раньше срока, составляем уравнение:
120
3х – 2х = 360,
х = 360
360: 40 = 9 (дней)
Ответ: 9 дней

Рефлексия

Домашнее задание
Выучить определения § 3, п. 8
Выполнить в тетради № 150, 151, 155

Использованные источники
https://resh.edu.ru/subject/lesson/7274/conspect/296573 /
https://reshator.com/sprav/algebra/7-klass/reshenie-zadach-s-pomoshchyu-linejnyh-uravnenij-s-odnoj-peremennoj /














































