Презентация к уроку математики "Геометрические фигуры и тела"

Геометрические фигуры и тела Выполнила учитель математики Шамилова З.С.

Основные понятия геометрии

• Точка — неопределяемое понятие геометрии, элемент пространства. Считается, что точка не имеет ни длины, ни ширины, ни площади.
• Прямая – основное неопределяемое понятие, подмножество пространства.
• Плоскость – основное неопределяемое понятие, специальное подмножество пространства.
• Геометрическая фигура – множество точек.

Свойства и взаимосвязи основных понятий описываются с помощью определенной группы аксиом.

Через основные понятия вводятся определения всех других геометрических понятий.

На основании аксиом и определений доказывают теоремы.

Основные понятия геометрии

Точка — неопределяемое понятие геометрии, элемент пространства. С точкой обычно знакомят методом показа — рисуют или прокалывают стержнем ручки в листочке бумаги. Считается, что точка не имеет ни длины, ни ширины, ни площади.

Прямая – основное неопределяемое понятие, подмножество пространства.

Плоскость – основное неопределяемое понятие, специальное подмножество пространства.

Геометрическая фигура – множество точек.

Свойства и взаимосвязи основных понятий описываются с помощью определенной группы аксиом. Через основные понятия вводятся определения всех других геометрических понятий. На основании аксиом и определений доказывают теоремы.

Геометрическое тело – это часть пространства, отделенная от остального пространства поверхностью – границей этого тела.

Геометрическим телом называют ограниченную связную фигуру в пространстве, которая содержит свои граничные точки, причем сколь угодно близко от любой граничной точки находятся внутренние точки фигуры.

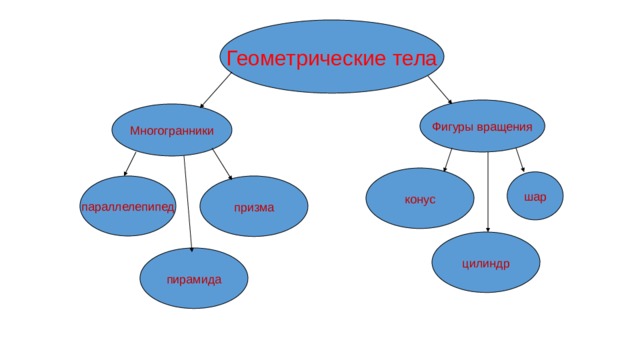
Геометрические тела

Фигуры вращения

Многогранники

конус

шар

призма

параллелепипед

цилиндр

пирамида

КЛАССИФИКАЦИЯ ГЕОМЕТРИЧЕСКИХ ТЕЛ

ГРАННЫЕ ГЕОМЕТРИЧЕСКИЕ ТЕЛА

ТЕЛА ВРАЩЕНИЯ

n-угольные призмы

Цилиндр

Конус

n-угольные пирамиды

Шар

Четырехугольники

Четырехугольник — ограничен ломаной из четырех звеньев, имеет четыре стороны и четыре вершины.

Фигура, состоящая из четырех точек и четырех последовательно соединяющих их отрезков, при этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются.

Параллелограмм – четырехугольник, противоположные стороны которого попарно параллельны.

Ромб –– параллелограмм, все стороны которого равны.

Четырехугольник — ограничен ломаной из четырех звень­ев, соответственно имеет четыре стороны и четыре вершины. Фигура, состоящая из четырех точек и четырех последовательно соединяющих их отрезков, при этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются.

Вершины четырехугольника называются соседними, если они являются концами одной из сторон.

Стороны четырехугольника, исходящие из одной вершины – соседние.

Параллелограмм – четырехугольник, противоположные стороны которого попарно параллельны.

Свойства:

середина диагонали является центром симметрии;

противоположные стороны равны;

противоположные углы равны;

каждая диагональ делит параллелограмм на два равных треугольника;

диагонали делятся точкой пересечения пополам.

Ромб – (от гр. «бубен») – параллелограмм, все стороны которого равны.

Свойства:

диагонали взаимно перпендикулярны;

диагонали ромба являются биссектрисами его углов (делят углы пополам);

прямая, содержащая диагональ ромба, является его осью симметрии;

имеет две оси симметрии – диагонали.

Прямоугольник — параллелограмм, у которого все углы прямые.

Свойства:

диагонали равны;

перпендикуляр, проходящий через середины противоположных сторон прямоугольника, является его осью симметрии;

имеет две оси симметрии – серединные перпендикуляры.

Квадрат — (от лат. «четырехугольник») прямоугольник, у которого все стороны равны.

Объединяет свойства параллелограмма, ромба и прямоугольника.

Имеет 4 оси симметрии – 2 диагонали и 2 серединных перпендикуляра.

Трапеция – (от лат. «столик») четырехугольник, две стороны которого параллельны, а две другие не параллельны.

Параллельные стороны – основания , непараллельные – боковые стороны .

Трапеция прямоугольная, если одна из боковых сторон перпендикулярна основанию.

Трапеция равнобочная, если ее боковые стороны равны. Углы при основании тоже равны.

Квадрат - прямоугольник, у которого все стороны равны.

Трапеция – четырехугольник, две стороны которого параллельны, а две другие не параллельны.

Прямоугольник — параллелограмм, у которого все углы прямые.

Тела вращения

• Тела вращения образуются при вращении

плоской фигуры вокруг не пересекающей ее оси,

имеют гладкие криволинейные поверхности.

• Прямой круговой цилиндр (гр. «валик,

каток») получается вращением прямоугольника

вокруг одной из сторон.

• Прямой круговой конус (лат. «шишка») –

вращением прямоугольного треугольника

вокруг катета.

• Шар – вращением полукруга вокруг диаметра.

Тела вра­щения образуются при вращении плоской фигуры вокруг не пересекающей ее оси, имеют гладкие криволинейные поверхности.

Шар, конус, цилиндр — это тела вращения.

Прямой круговой цилиндр (гр. «валик, каток») получается вращением прямоугольника вокруг одной из сторон.

Прямой круговой конус (лат. «шишка») – вращением прямоугольного треугольника вокруг катета.

Шар – вращением полукруга вокруг диаметра.

Пирамиды

• Пирамида – многогранник, одна из граней которого – произвольный многоугольник, а остальные – треугольники, имеющие общую вершину.
• Пирамида правильная, если в ее основании правильный многоугольник, а основание высоты совпадает с центром основания.
• Высота – отрезок перпендикуляра, проведенный из вершины пирамиды к плоскости ее основания.
• Усеченная пирамида – часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию.

Построение изображения пирамиды (на примере правильной пирамиды):

• строят основание, находят его центр;
• строят высоту, проводя отрезок из центра основания, отмечают на нем вершину пирамиды;
• соединяют отрезками вершины основания с вершиной пирамиды.

Пирамида – многогранник, одна из граней которого – произвольный многоугольник, а остальные – треугольники, имеющие общую вершину.

Пирамида правильная, если в ее основании правильный многоугольник, а основание высоты совпадает с центром основания.

Высота – отрезок перпендикуляра, проведенный из вершины пирамиды к плоскости ее основания.

Усеченная пирамида – часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию.

Построение изображения пирамиды:

На примере правильной пирамиды

строят основание, находят его центр;

строят высоту, проводя отрезок из центра основания, отмечают на нем вершину пирамиды;

соединяют отрезками вершины основания с вершиной пирамиды.

Призмы

• Призма – (гр. «отпиленный кусочек») многогранник, две грани которого – равные многоугольники, лежащие в параллельных плоскостях, а остальные грани – параллелограммы.
• Если боковые ребра перпендикулярны плоскостям оснований, то призма – прямая; если нет – наклонная.
• Если в основании прямой призмы лежит правильный многоугольник, то призма – правильная.
• Параллелепипед – призма, основания которой - параллелограммы.
• Прямоугольный параллелепипед – прямой параллелепипед, основание которого – прямоугольник. Все грани – прямоугольники.
• Куб – прямоугольный параллелепипед, все ребра которого равны. Все грани – квадраты.

Построение изображения призмы:

• строят основание (нижнее или верхнее – многоугольник);
• из вершин многоугольника строят параллельные прямые;
• на прямых откладывают равные отрезки (высота призмы);
• соединяют полученные точки (концы отрезков), получая второе основание.

Призма – (гр. «отпиленный кусочек») многогранник, две грани которого – равные многоугольники, лежащие в параллельных плоскостях, а остальные грани – параллелограммы.

Если боковые ребра перпендикулярны плоскостям оснований, то призма – прямая; если нет – наклонная.

Если в основании прямой призмы лежит правильный многоугольник, то призма – правильная.

Параллелепипед – призма, основания которой - параллелограммы.

Прямоугольный параллелепипед – прямой параллелепипед, основание которого – прямоугольник. Все грани – прямоугольники.

Куб – прямоугольный параллелепипед, все ребра которого равны. Все грани – квадраты.

Построение изображения призмы:

строят основание (нижнее или верхнее – многоугольник);

из вершин многоугольника строят параллельные прямые;

на прямых откладывают равные отрезки (высота призмы);

соединяют полученные точки (концы отрезков), получая второе основание.

Сфера и шар

Сфера – поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки – центра сферы.

Радиус сферы – отрезок, соединяющий центр и любую точку сферы.

Диаметр сферы – отрезок, соединяющий две точки сферы и проходящий через ее центр.

Шар – тело, ограниченное сферой – множество точек пространства, расположенных от данной точки на расстоянии, не большем данного.

Шаровой сегмент – часть шара, отсекаемая от него плоскостью.

Шаровой слой – часть шара, расположенная между двумя параллельными плоскостями, пересекающими шар.

Сфера – поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки – центра сферы .

Радиус сферы – отрезок, соединяющий центр и любую точку сферы.

Диаметр сферы – отрезок, соединяющий две точки сферы и проходящий через ее центр.

Шар – тело, ограниченное сферой – множество точек пространства, расположенных от данной точки на расстоянии, не большем данного.

Шаровой сегмент – часть шара, отсекаемая от него плоскостью.

Шаровой слой – часть шара, расположенная между двумя параллельными плоскостями, пересекающими шар.

Многие думают, что различные геометрические тела, замысловатые линии и поверхности можно встретить только в книгах ученых-математиков.

Однако стоит внимательно всмотреться и мы сразу обнаружим вокруг нас всевозможные геометрические фигуры. И, таким образом можно сделать вывод: нас всегда окружали, окружают и будут окружать множество геометрических тел…