Презентация: "Объем конуса"

Тела вращения

Шар

Конус

Цилиндр

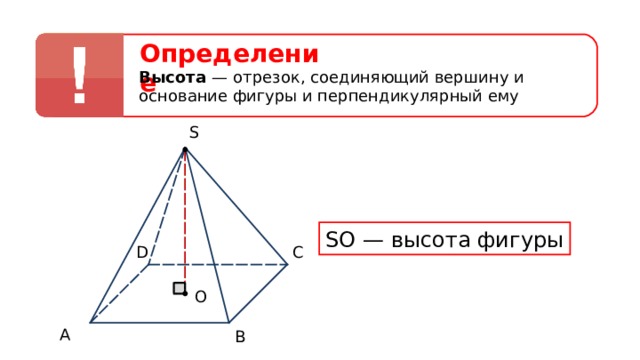
Определение

Высота — отрезок, соединяющий вершину и основание фигуры и перпендикулярный ему

S

SO — высота фигуры

D

С

O

А

В

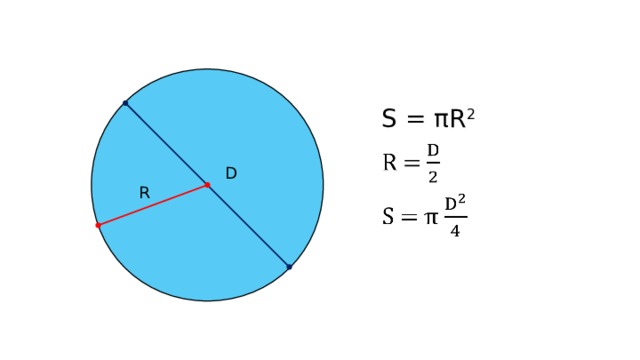
S = π R 2

D

R

Определение

Конусом называется тело, которое состоит из круга — основания конуса, точки,

не лежащей в плоскости этого круга, вершины конуса и всех отрезков, соединяющих вершину конуса с точками основа­ния

Теорема

Объём конуса равен одной трети произведения площади основания на высоту

Теорема

Объём конуса равен одной трети произведения площади основания на высоту

Дано :

O

конус

ОМ 1 = х, OM = h

S — площадь его основания

h — высота конуса

x

V — объём конуса

α

R 1

h

S(x)= π R 1 2

Доказательство:

M 1

A 1

О X — ось конуса через ОМ

α ⏊ О X ⇒ сечение конуса

М 1 — центр,

R 1 — радиус

R

S ( x ) — площадь сечения

х — абсцисса М 1

M

A

ΔОМ 1 A 1 ∼ ΔОМА (∠ОМ 1 A 1 = ∠ ОМА — прямые, ∠МОА — общий) ⇒

X

Теорема доказана

Формула объёма усечённого конуса

O 1

V — объём усеченного конуса

h — высота

S и S 1 — площади оснований

R 1

h

R

O

Задача 1

Дано:

Δ прямоугольный

R

4

3

4

а = 4, b = 3

Найти:

V конуса: 1) R = a, 2) R = b

h

4

Решение:

3

1) R — радиус основ. конуса

2) R = b = 3, h = a = 4

h — высота конуса

R = а = 4, h = b = 3

S осн . = πR 2

h

4

S осн . = πR 2

R

V = πR 2 h

3

3

Ответ: V = 16 π или V = 1 2 π

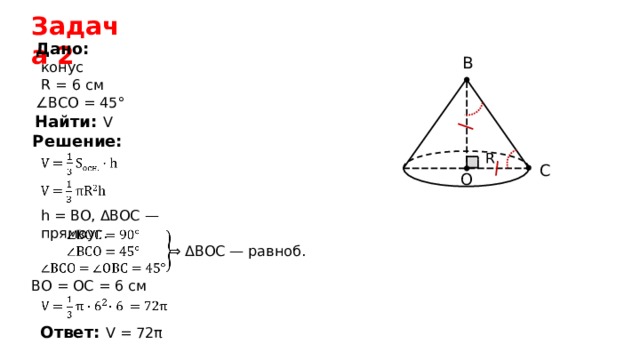
Задача 2

Дано:

B

конус

R = 6 см

∠ ВСО = 45°

Найти: V

Решение:

R

C

O

h = BO, ΔBOC — прямоуг .

⇒ ΔBOC — равноб .

BO = OC = 6 см

Ответ: V = 7 2 π