Презентация "Общие методы решения уравнений. (алгебра,11 класс)

• «Правильному применению методов можно научиться только применяя их на разнообразных примерах»

Г. Цейтен

• 11 класс

Общие методы решения уравнений

• УМК А.Г. Мордкович (профильный уровень)

Цели урока:

• Рассмотреть общие методы решения уравнений.
• Научиться применять эти методы при решении уравнений.
• Формировать навыки применение наиболее рациональных способов решения уравнений.

Рассмотрим уравнения:

1) х ² - 2 х = 0;

2) sin²x + sinx = 0 ;

3)

Рассмотрим уравнения:

Общие методы решения уравнений:

• Замена уравнения h(f(x)) = h(g(x)) уравнением f(x) = g(x) .
• Метод разложения на множители.
• Метод введения новой переменной.
• Функционально-графический метод.

0, а≠1) к уравнению f(x) = g(x) ; при решении логарифмических уравнений, когда переходили от уравнения log f(x) = log g(x) к уравнению f(x) = g(x) ; при решении иррациональных уравнений, когда переходили от уравнения к уравнению f(x) = g(x) . " width="640"

1. Замена уравнения h(f(x)) = h(g(x)) уравнением f(x) = g(x) .

Этот метод мы применяем:

• при решении показательных уравнений, когда переходили от уравнения (а 0, а≠1) к уравнению f(x) = g(x) ;
• при решении логарифмических уравнений, когда переходили от уравнения log f(x) = log g(x) к уравнению f(x) = g(x) ;
• при решении иррациональных уравнений, когда переходили от уравнения к уравнению f(x) = g(x) .

Пример 1:

Решить уравнение

Ответ: 0; 1,5.

Пример 2:

2. Метод разложения на множители.

Уравнение f(x)g(x)h(x) = 0 можно заменить совокупностью уравнений:

Решив уравнения этой совокупности, нужно взять те их корни, которые принадлежат ОДЗ исходного уравнения, а остальные отбросить как посторонние.

Пример 3:

Решить уравнение

Пример 3:

Из найденных корней этой системе неравенств удовлетворяет только

х = 9, остальные являются посторонними для данного уравнения.

Ответ: 9.

3. Метод введения новой переменной.

Если уравнение f(x)= 0 удалось преобразовать к виду p(g(x)) = 0 , то нужно ввести новую переменную u = g(x) , решить уравнение p(u) = 0, а затем решить совокупность уравнений:

где и , и ,… и - корни уравнения р(и) = 0.

Пример 4:

Решить уравнение

Введём новую переменную .

Получим:

Освободившись от знаменателей, получим:

Пример 4:

Найдём корни квадратного уравнения:

Выполним проверку корней на выполнение условия:

5(у – 3)(у + 1) ≠ 0 .

Оба корня удовлетворяют данному условию.

Пример 4:

Вернёмся к замене переменной и решим два уравнения:

и

Ответ:

3. Функционально-графический метод.

Чтобы графически решить уравнение f(x) = g(x) нужно построить графики функций

у = f(x) и у = g(x) и найти точки их пересечения. Корнями уравнения служат абсциссы этих точек.

Пример 5:

1) Решить уравнение = | x – 2 |

1 шаг : построить графики функций у = и у = | x – 2 |

2 шаг: найти абсциссы точек (или точки) пересечения графиков

Ответ: x 1 = 1, х 2 = 4

2. x 3 – 5 + х = 0

Пример 6 :

х 3 = 5 - х

f(x) = х 3

g(x) = 5 - х

х ≈ 1,5

Решением является абсцисса точки пересечения графиков левой и правой частей уравнения

Графические методы решения уравнений

Построение графиков функций левой и правой частей уравнения (решением является абсциссы точек (точки) пересечения графиков)

Функционально – графические методы

Использование свойств функций левой и правой частей уравнения (монотонность, четность, нечетность)

Использование ограниченности функций левой и правой частей уравнения (метод оценки)

Пример 7:

Решить уравнение

Рассмотрим функцию у = х ² - 2х + 2. Её графиком является парабола, ветви которой направлены вверх.

В вершине параболы функция достигает своего наименьшего значения.

Пример 7:

Найдём координаты вершины параболы.

Для функции у = х ² - 2х + 2

Функция у = cos 2 π x обладает свойством:

Пример 7:

Задача сводится к решению системы уравнений

х ² - 2х + 2 = 1,

cos 2 π x = 1.

Решив 1 уравнение получили: х = 1. Это значение удовлетворяет и 2 уравнению системы, следовательно, является единственным корнем заданного уравнения.

Ответ: 1.

Мы рассмотрели общие методы решения уравнений, примеры применения этих методов.

Перейдём к практической работе.

Решаем № 27.5 (в), 27.9 (б), 27.12 (б), 27.14 (а), 27.19 (б), 27.21 (а), 27.25 (а,б).

№ 27.25 (а)

Ответ: одно решение

x 2 + 1 = cos x

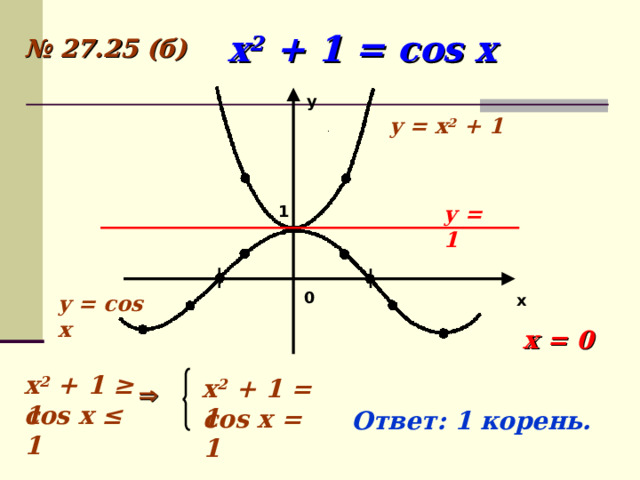
№ 27.25 (б)

у

y = x 2 + 1

y = 1

1

0

y = cos x

х

x = 0

x 2 + 1 ≥ 1

x 2 + 1 = 1



cos x ≤ 1

cos x = 1

Ответ: 1 корень.

Подведем итоги

Общие методы решения

уравнений

Функционально-графические

Аналитические

По графику

По свойствам

1

3

2