Презентация " Виды уравнений и способы их решений"

Урок алгебры в 9 классе Виды уравнений и способы их решения

«Учиться можно только весело, чтобы переваривать знания, нужно поглощать их с аппетитом»

А.Франс

ВИДЫ УРАВНЕНИЙ И СПОСОБЫ ИХ РЕШЕНИЯ

Цель:

• повторить теорию, выработать умение определять вид уравнения и выбирать рациональный способ решения данного уравнения

Мне приходится делить своё время между политикой и уравнением. Однако уравнение, по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнение будет существовать вечно.

Альберт Эйнштейн

Теоретическая разминка

• Что такое уравнение?
• Что, значит, решить уравнение?
• Что называют корнем уравнения?
• Какие виды уравнений вы знаете?

0 a≠1 6.Иррациональные уравнения 11.Логарифмическое уравнение 10.Уравнение с параметрами ax=10 9.Уравнение с модулем |y+2|=16 " width="640"

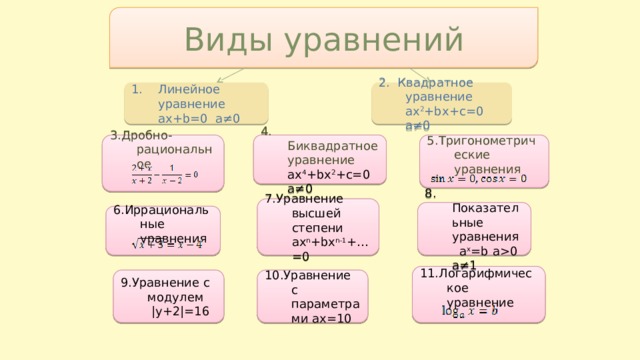
Виды уравнений

2. Квадратное уравнение ax 2 +bx+c=0 a≠0

• Линейное уравнение ax+b=0 a≠0

4. Биквадратное уравнение ax 4 +bx 2 +c=0 a≠0

5.Тригонометрические уравнения

3.Дробно-рациональное

7.Уравнение высшей степени ax n +bx n-1 +…=0

8. Показательные уравнения

a x =b a0 a≠1

6.Иррациональные уравнения

11.Логарифмическое уравнение

10.Уравнение с параметрами ax=10

9.Уравнение с модулем

|y+2|=16

5 класс

• Нахождение неизвестных компонентов.
• а+х=в х=в-а
• х-а=в х=в+а
• а-х=в х=а-в
• а ∙х=в х=в:а
• а:х=в х=а:в
• х:а=в х=а∙в

6 класс

• 7(3х-1)=5(х-3)

• Раскрыть скобки; 21х-7=5х-15
• Вправо-с переменной, 21х-5х=-15+7

влево - числа (меняя знак);

• Привести подобные; 16х=-8
• Найти неизвестный

множитель; х=-0,5

• Записать ответ. Ответ: х=-0,5

6 класс Пропорция

• Пропорцией называется равенство двух отношений.
• a : b = c : d
• Основное свойство пропорции

• 15,2 : х = 3,8 : 0,5

• a ∙ d = b ∙ c

• 15,2 ∙ 0,5 = 3,8 ∙ х

• х= 15,2 ∙0,5 : 3,8

• х=2

• Ответ: х=2

7 КЛАСС Линейные уравнения

ах+b=0

• а ≠0; х=-b/a.

• a=0,b=0; х-любое число.

• а=0, b≠0; нет корней.

Определение:

• Квадратным уравнением (или уравнением второй степени) называется уравнение вида ax²+bx+c=0 , где

x – переменная,

a, b и c – некоторые числа,

причем a≠0

0 , то х 1 = х 2 = D , то квадратное уравнение решений не имеет D=0 , то х 1,2 = - " width="640"

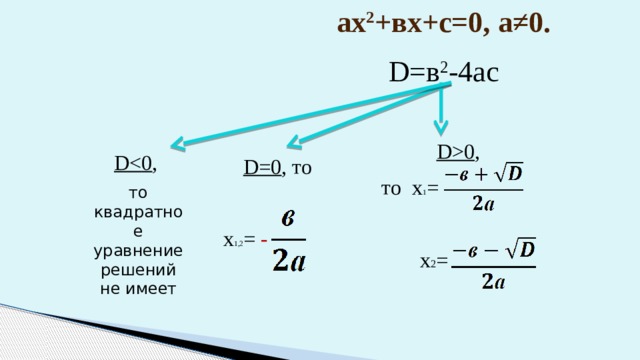
ах 2 +вх+с=0, а ≠0.

D=в 2 -4ас

D0 ,

то х 1 =

х 2 =

D ,

то квадратное уравнение решений не имеет

D=0 , то

х 1,2 = -

8 КЛАСС Квадратные уравнения

Неполным квадратным уравнением называют уравнение, в котором хотя бы один из коэффициентов b или c равен нулю.

• -2 x ²+7=0 , b =0
• 3 x ²-10 x =0 , c =0
• 4 x ²=0 , b =0 и c =0

Виды неполных квадратных уравнений

• ax²+c=0 ,где c≠0
• ax²+bx=0 ,где b≠0
• ax²=0

• -3x²+15=0

-3x²=-15

x²=5

x₁=√5 x₂=-√5

• 4x²+9x=0

x(4x+9)=0

x₁=0 или 4x+9=0

4x=-9

x₂= 2¼

• 4x²+3=0

4x²=-3

x²=-¾ - нет корней, а значит и 4x²+3=0 –не имеет корней

Примеры:

Уравнения, приводимые к квадратным

Уравнения, приводимые к квадратным

• Ищем уравнение с переменно, которое входит в уравнение дважды
• Заменяем это выражение другой переменной. Решаем уравнение относительно новой переменной.
• Возвращаемся к нашей подстановке. Решаем уравнение относительно данной в уравнении переменной.

Рассмотрим решение уравнений высших степеней, используя разложение на множители .

ПРИМЕР :

• Разложим левую часть уравнения на множител и:

• Когда произведение множителей равно нулю?

• Ответ : -1; -0,5; 1.

1)(х-9) 2 -8(х-9)+7=0

а = х-9

2) (у 2 +2у+4) – 7(у 2 +2у+4)+12=0

а = у 2 +2у+4

3) (х 2 +х+1) 2 - 3х 2 - 3х- 3=0

а = х 2 +х+1

4) (х 2 -5х+7) 2 - (х-2)(х-3)=1

а = х 2 -5х+7

9 КЛАСС Дробно рациональные уравнения

1) Найти общий знаменатель всех имеющихся дробей;

2) заменить данное уравнение целым, умножив обе его части на общий знаменатель;

3) решить полученное целое уравнение;

4) исключить из его корней те, которые обращают в нуль общий знаменатель;

5) записать ответ.

Когда уравненье решаешь, дружок,

Ты должен найти у него корешок.

Значение буквы проверить несложно,

Поставь в уравненье его осторожно.

Коль верное равенство выйдет у вас,

То корнем значенье зовите тотчас .

О Севостьянова

Спасибо за работу

на уроке