Презентация "Материалы к урокам алгебры 9 класс"

Материалы

к урокам алгебры

9 класс

Учитель Козина Н.А.

Функция y = ax 2 , её график и свойства.

Квадратичная функция. Определение.

Квадратичной функцией называется функция, которую можно задать формулой вида

y = ax 2 + bx + c,

где x – независимая переменная, a, b и c – некоторые числа, причем a  0.

Квадратичная функция. Примеры.

• Зависимость пути от времени при равноускоренном движении.

Частный случай квадратичной функции

• y = ax 2

y = x 2

y = 2x 2

0. 1) Если x=0, то y=0. График функции проходит через начало координат. 2) Если x  0, то y0. График функции расположен в верхней полуплоскости. " width="640"

Свойства функции y = ax 2 при a 0.

• 1) Если x=0, то y=0. График функции проходит через начало координат.
• 2) Если x  0, то y0. График функции расположен в верхней полуплоскости.

0. 3) Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси y. " width="640"

Свойства функции y = ax 2 при a 0.

• 3) Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси y.

0. 4) Функция убывает в промежутке (-  ;0] и возрастает в промежутке [0;+  ). " width="640"

Свойства функции y = ax 2 при a 0.

• 4) Функция убывает в промежутке (-  ;0] и возрастает в промежутке [0;+  ).

0. 5 ) Наименьшее значение равное нулю, функция принимает при x=0, наибольшего значения функция не имеет. Областью значений функции является промежуток [0;+  ). " width="640"

Свойства функции y = ax 2 при a 0.

• 5 ) Наименьшее значение равное нулю, функция принимает при x=0, наибольшего значения функция не имеет.
• Областью значений функции является промежуток [0;+  ).

Свойства функции y = ax 2 при a

• 1) Если x=0, то y=0. График функции проходит через начало координат.
• 2) Если x  0, то y

Свойства функции y = ax 2 при a

• 3) Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси y.

Свойства функции y = ax 2 при a

• 4) Функция убывает в промежутке [0;+  ) и возрастает в промежутке (-  ;0].

Свойства функции y = ax 2 при a

• 5 ) Наибольшее значение равное нулю, функция принимает при x=0, наименьшего значения функция не имеет.
• Областью значений функции является промежуток (-  ;0].

Функция y = ax 2 , её график и свойства.

• № 73

К уроку № 9

Функция y = ax 2 , её график и свойства.

№ 75

y = x 2

y = 1,8x 2

К уроку №9

Укажите какие-нибудь два значения переменной x, которым соответствуют равные значения функции:

x=2

x=-2

Не выполняя вычислений, сравните значения выражений:

=

Известно, что график функции проходит через точку (-8;-16).

Определите знак коэффициента а;

“ -”

Укажите координаты еще одной точки графика этой функции.

(8; -16)

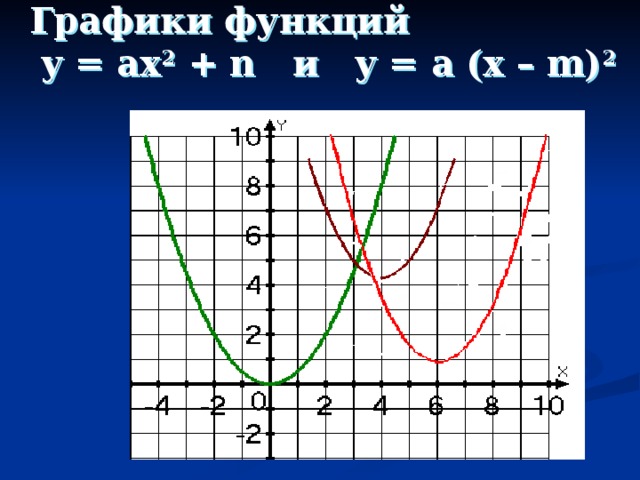
Графики функций y = ax 2 + n и y = a (x – m) 2

0, или на –n единиц вниз, если n " width="640"

Графики функций y = ax 2 + n и y = a (x – m) 2

Правило.

График функции y = ax 2 + n является параболой, которую можно получить из графика функции y = ax 2 с помощью параллельного переноса вдоль оси y на n единиц вверх, если n 0, или на –n единиц вниз, если n

0, или на –m единиц влево, если m " width="640"

Графики функций y = ax 2 + n и y = a (x – m) 2

Правило.

График функции y = a (x – m) 2 является параболой, которую можно получить из графика функции y = ax 2 с помощью параллельного переноса вдоль оси x на m единиц вправо, если m 0, или на –m единиц влево, если m

0, или на –m единиц влево, если m 0, или на –n единиц вниз, если n " width="640"

График функции y = a (x – m) 2 + n

Правило.

График функции y = a (x – m) 2 + n является параболой, которую можно получить из графика функции y = ax 2 с помощью двух параллельных переносов: сдвига вдоль оси x на m единиц вправо, если m 0, или на –m единиц влево, если m 0, или на –n единиц вниз, если n

График функции y = a (x – m) 2 + n

Правило.

Производить параллельные переносы можно в любом порядке.

График функции y = f (x – m) + n можно получить из графика y = f (x) с помощью двух соответствующих параллельных переносов.

№ 87 а

№ 87 а

№ 88

№ 88