Муниципальное бюджетное общеобразовательное учреждение
«Отрадненская средняя общеобразовательная школа №2»
Проект по математике
Линейная функция
Выполнила: ученица 7А класса
Конакова Анастасия
Руководитель: учитель
математики Карпенко Н.Р.
Отрадное – 2017
СОДЕРЖАНИЕ
Введение………………………………………………………………….. 3
Как развивалось понятие функции …………………………………… 4
Определение линейной функции и её свойства …………………… 7
Применение линейной функции в различных областях знаний ……11
Математика ………………………………………………… 11
Физика ………………………………………………………… 12
Биология, экология, медицина ……………………………… 15
География …………………………………………………….. 15
Применение линейной функции в повседневной жизни …………. 16
Заключение………………………………………………………………. 21
Список использованных источников …………………………………. 22
ВВЕДЕНИЕ
На уроках алгебры в этом учебном году мы познакомились с понятием линейной функции, её графиком и свойствами, узнали частные случаи линейной функции и от чего зависит взаимное расположение графиков линейных функций. Также мы узнали, что линейную функцию можно назвать важнейшей, так как много законов природы и практических взаимосвязей выражается с помощью этой функции.
Цель: показать многогранность применения линейной функции в различных сферах человеческой деятельности.
Задачи:
– обобщить имеющиеся знания о линейной функции;
– найти новые сведения о линейной функции и её свойствах из различных источников информации;
– узнать, в каких областях знаний находит применение линейная функция;
– установить, находит ли применение линейная функция в повседневной жизни людей.
Гипотеза: линейная функция может применяться не только в математике а и в других науках, включая повседневную жизнь.
I.КАК РАЗВИВАЛОСЬ ПОНЯТИЕ ФУНКЦИИ
Функция – одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.
Высокого уровня математические знания достигли в Древнем Вавилоне. Для облегчения вычислений при учёте налогов, возведении своих дворцов и т.д. вавилоняне составили громоздкий комплект специальных арифметических таблиц: таблицы обратных значений чисел, таблицы квадратов и кубов и даже таблицы для суммы квадратов чисел и их кубов. Однако путь от появления таблиц до создания общего понятия функциональной зависимости был ещё очень долог.
В Древней Греции в отличие от Вавилона появились профессиональные ученые, которые изучали саму математическую науку. Древнегреческие математики нашли много различных кривых, неизвестных вавилонянам, изучали зависимости между отрезками диаметров и хорд в круге, эллипсе и других линиях, но всё же не создали общего понятия функции.
Только начиная с XVII века, в связи с проникновением в математику идеи переменных, понятие функции применяется явно и вполне сознательно.


Рене Декарт
Путь к появлению понятия функции заложил в XVII веке французский философ и математик Рене Декарт (1596–1650). Он первый ввёл в математику понятие переменной величины. Чтобы освободить алгебру от геометрического языка, Декарт ввёл фиксированный единичный отрезок и стал рассматривать отношение других отрезков к нему. Он установил соответствия между числами и отрезками на прямой и, таким образом, ввел алгебраический метод в геометрию. Появилась возможность изображать зависимость величин графически на координатной плоскости, числа – отрезками. При записи зависимостей между величинами, он стал применять буквы: для переменных и неизвестных величин Декарт принял обозначения x, y, z, …, а для величин известных и постоянных – a, b, c и т.д. Как известно, эти обозначения применяются в математике до сегодняшнего дня. Отношения между известными и неизвестными величинами Декарт выражал в виде уравнений, в которых все величины заменил длинами отрезков. Он обратил внимание на то, что кривая на плоскости характеризуется уравнением, обладающим тем свойством, что координаты любой точки, лежащей на этой линии, удовлетворяют данному уравнению. Одновременно с Декартом к мысли о соответствии между линиями и уравнениями пришел другой французский математик Пьер Ферма (1601–1665). В их работах появляется отчетливое представление прямоугольной системы координат. В своей «Геометрии» в 1637 году Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы.
В 1671 году И. Ньютон (1643–1727) под функцией стал понимать переменную величину, которая изменяется с течением времени (он называл её «флюентой»).
Но у Декарта, как и у его современников, понятие функции носило по существу интуитивный характер и было связано либо с геометрическими (ординаты точек кривых – функция от абсцисс x), либо с механическими (путь и скорость – функция от времени t) представлениями.
С амо слово «функция» (от латинского functio – совершение, выполнение) впервые было употреблено немецким математиком Лейбницем (1646–1716) в 1673 г. в письме к Х. Гюйгенсу (1629–1695) (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону), а в печати введено с 1694 года. Начиная с 1698 года, Лейбниц ввел также термины «переменная» и «константа».
амо слово «функция» (от латинского functio – совершение, выполнение) впервые было употреблено немецким математиком Лейбницем (1646–1716) в 1673 г. в письме к Х. Гюйгенсу (1629–1695) (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону), а в печати введено с 1694 года. Начиная с 1698 года, Лейбниц ввел также термины «переменная» и «константа».
В XVIII веке появился новый взгляд на функцию как на формулу, связывающую одну переменную с другой. Подход к такому определению впервые сделал швейцарский математик Иоганн Бернулли (1667–1748), который в 1718 году определил функцию следующим образом: «функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных».
О кончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Леонард Эйлер. «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств». Так понимали функцию на протяжении почти всего 18 века французские математики Жан Лерон Даламбер (1717–1783), Жозеф Луи Лагранж (1736–1813), Жан Батист Жозеф Фурье (1768–1830) и другие видные математики.
кончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Леонард Эйлер. «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств». Так понимали функцию на протяжении почти всего 18 века французские математики Жан Лерон Даламбер (1717–1783), Жозеф Луи Лагранж (1736–1813), Жан Батист Жозеф Фурье (1768–1830) и другие видные математики.
Большой вклад в разрешение спора Эйлера, Даламбера, Бернулли и других ученых XVIII века по поводу того, что стоит понимать под функцией, внёс Фурье. Из его трудов следовало, что любая кривая независимо от того, из скольких и каких разнородных частей она состоит, может быть представлена в виде единого аналитического выражения, и что имеются также прерывные кривые, изображаемые аналитическим выражением.
После работы Фурье стало ясно, что несущественно, каким аналитическим выражением задана функция, что это только, как говорят философы, кажимость (от слова «казаться»). А существо дела в том, какие значения принимает функция при заданных значениях аргумента. После длительного уточнения этой идеи, в которой приняли участие Фурье, Н.И. Лобачевский (1792–1856), немецкий математик Иоганн Дирихле (1805–1859) и другие ученые, общепризнанным стало следующее определение: переменная величина у называется функцией переменной величины х, если каждому значению величины х соответствует единственное определенное значение величины у.
II. ОПРЕДЕЛЕНИЕ ЛИНЕЙНОЙ ФУНКЦИИ И ЕЁ СВОЙСТВА
Линейной функцией называется функция, которую можно задать формулой вида y=аx + b,
где y – зависимая переменная (функция);
x – независимая переменная (аргумент);
а и b – некоторые числа (коэффициенты).
Графиком линейной функции y=аx+b является прямая линия, располагающаяся относительно координатных осей различным образом в зависимости от постоянных коэффициентов а и b, которые могут принимать положительные или отрицательные значения или быть равным нулю. Для построения графика линейной функции можно найти две точки прямой на плоскости, например, точки пересечения с осями координат, или воспользоваться геометрическим смыслом коэффициентов а и b.
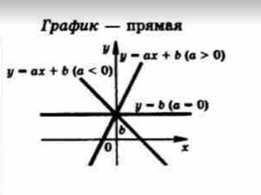
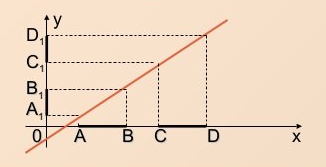
Основное свойство линейной функции: равным изменениям одной величины соответствуют равные изменения другой величины (приращение функции пропорционально приращению аргумента).
Свойства линейной функции:
При а 0, функция возрастает (график идет сверху вниз);
при а
Частным случаем линейной функции является прямая пропорциональность. Прямой пропорциональностью называется функция, которую можно задать формулой у = kх (k ≠ 0, b = 0). График прямой пропорциональности представляет собой прямую линию, проходящую через начало координат.
Свойством линейной функции y=kx + b является тангенс угла, который образует прямая с положительным направлением оси абсцисс, при этом k – угловой коэффициент (угол наклона прямой к оси х), а число b является показателем ординаты точки пересечения прямой с осью ординат.
.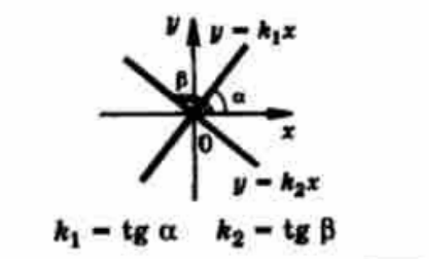
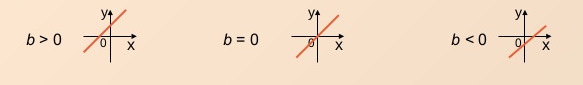 При k 0, прямая образует острый угол с осью абсцисс:
При k 0, прямая образует острый угол с осью абсцисс:
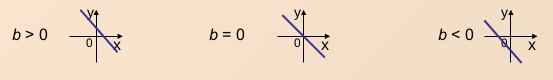 При k
При k
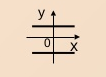
При k = 0, прямая параллельна оси абсцисс:
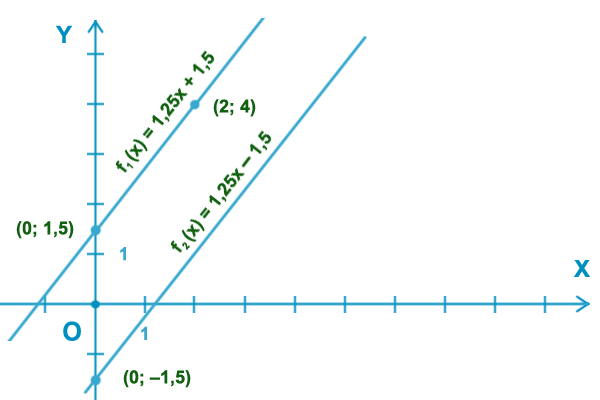
На следующем рисунке видно, что равенство коэффициентов k – условие
параллельности прямых, а число b – ордината точки пересечения с осью OY .
III. ПРИМЕНЕНИЕ ЛИНЕЙНОЙ ФУНКЦИИ
В РАЗЛИЧНЫХ ОБЛАСТЯХ ЗНАНИЙ
Важным моментом изучения линейной функции является выделение приложений линейной функции в различных областях человеческого знания (геометрия, физика, биология, география, астрономия, экономика и т.д.).
3.1. Математика
1. Зависимость длины окружности (C) от её радиуса (r) (чем больше радиус, тем больше длина окружности):
C=2 π r,
где p»3,14.
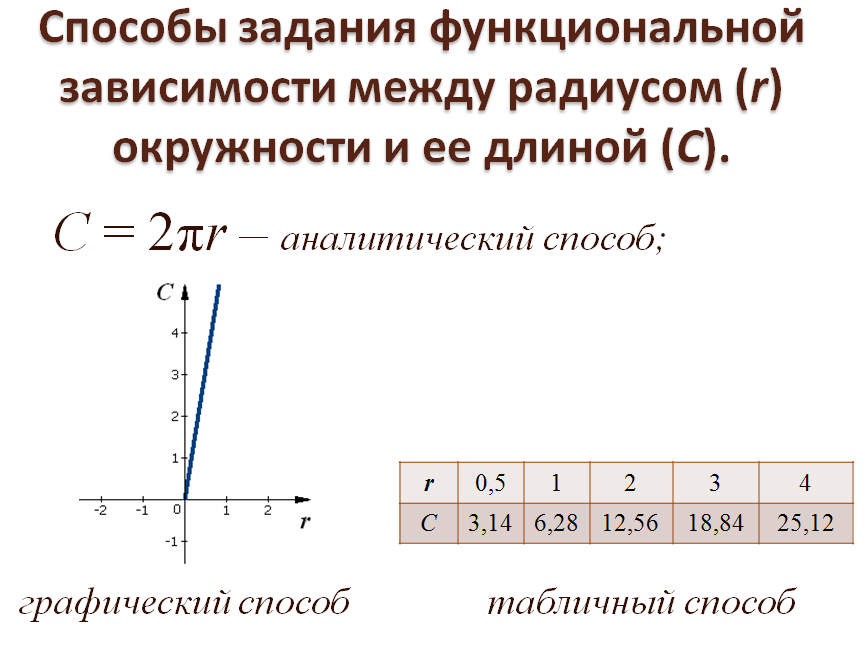
Эта линейная функция является прямой пропорциональностью с угловым коэффициентом, равным k =2 π.
3.2. Физика
С помощью линейной функции описываются многие физические процессы.
1. Зависимость расстояния (s) от времени движения (t) (чем больше время движения при постоянной скорости (v), тем больше пройденный путь):
s=vt; s=s0 +vt.
2. Зависимость веса тела (Р) от его массы (m) (чем больше масса, тем больше вес тела):
P = mg,
где g – ускорение свободного падения 9,81 м/с2.
3. Зависимость давления жидкости на дно сосуда (P) от высоты столба жидкости (h) – линейная зависимость и задаётся формулой:
P=gρh,
где ρ – плотность жидкости.
3.3. Биология
Зависимость длины волос человека от количества дней:
l=l0+0,4t,
где l – длина волос (мм), l0 – первоначальная длина волос (мм), t – количество дней, 0,4 – скорость роста волос в сутки (мм).
3.4. География
Зависимость расстояния на местности от расстояния на карте (масштабирование):
S=1000c,
где S – расстояние на местности (км), с – расстояние на карте (см), 1000 – масштаб карты (км/см).
IV. ПРИМЕНЕНИЕ ЛИНЕЙНОЙ ФУНКЦИИ
В ПОВСЕДНЕВНОЙ ЖИЗНИ
Расчет в магазине за купленные товары
Все мы совершаем покупки, чтобы удовлетворить свои потребности. Чем больше мы купим вещей, тем больше мы заплатим за покупку.
Потребление электроэнергии.
Абсолютно все пользуются электроприборами. Они потребляют энергию. Чем дольше мы используем электроприборы, тем больше потребляем энергии. Соответственно и платим больше. Эта зависимость выражается формулой П=к*N, где к- стоимость одного киловатт-часа, N- количество часов.)
Потребление пищи.
Всем необходимо есть, чтобы у нас были силы и энергия для работы. Эту энергию мы получаем из еды. Чем больше мы съедим, тем больше энергии получим.
ЗАКЛЮЧЕНИЕ
В ходе работы над проектом я приобрела и систематизировала новые знания о линейной функции, узнала много нового о применении линейной зависимости в окружающем мире, научилась использовать линейную функцию в практической деятельности, расширила свой кругозор.
Я изучила историю возникновения и этапы развития понятия «функция». Узнала много интересного о великих математиках XVII – XIX веков.
На большом количестве примеров я показала, что линейная функция является математической моделью обширного класса процессов, происходящих в реальной действительности, и описывает зависимости между реальными величинами не только в математике, но и во многих других науках (физике, биологии, географии, экологии, медицине и др.). Зависимости пути от времени при равномерном прямолинейном движении, сопротивление металлов от температуры, давление жидкости на дно сосуда от высоты столба жидкости, зависимость силы упругости от деформации тела, численность сине-зелёных водорослей от концентрации общего фосфора в воде и многие другие выражаются линейной функцией. Конечно, нельзя считать эти исследования исчерпывающими, так как областей науки и техники, где применяется линейная функция, значительно больше.
Также я провела работу по выявлению линейных зависимостей в своей повседневной жизни. Оказалось, что линейные зависимости встречаются прямо вокруг нас: и в обычных продуктах питания, и при измерении артериального давления, и даже в спорте. Эта работа оказалась увлекательной и интересной. Я научилась применять свои знания о линейной функции на практике.
Я думаю, что этот проект будет интересен людям, желающим расширить свои знания об изучаемой в школе линейной функции, её разнообразной прикладной направленности и большой значимости в различных областях деятельности человека.
Выражаю благодарность руководителю за постановку задачи и полезные советы.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Нагибин Ф.Ф. Математическая шкатулка : пособие для учащихся 4 – 8 кл. сред. шк. / Ф.Ф. Нагибин, Е.С. Канин. – 5-е изд. – М. : Просвещение, 1988. – 160 с.
2. Виленкин, Н. Я. Функции в природе и технике : книга для внеклассного чтения IX–X классов / Н. Я. Виленкин. – 2-е изд., испр. – М. : Просвещение, 1985. – 192 с.
3. Колягин Ю.М. Алгебра. 7 класс : учебник для общеобразовательных учреждений / Ю.М. Колягин, М.В. Ткачёва, Н.Е. Фёдорова, М.И. Шабунин. – М. : Просвещение, 2012. – 319 с.
4. Звавич Л.И. Алгебра в таблицах. 7—11 классы : справочное пособие / Л.И. Звавич, А.Р. Рязановский. – 8-е издание. – М. : Дрофа, 2004. – 96 с.
5. Перышкин А.В. Физика : учебник для 6-7 классов средней школы / А.В. Перышкин, Н.А. Родина. – М. : Просвещение, 1982. – 320 с.
6. Кикоин И.К. Физика : учебник для 8 класса средней школы / И.К. Кикоин, А.К. Кикоин. – 8-е издание. – М. : Просвещение, 1986. – 240 с.
7. Дневник гимнастки
8. Интернет-ресурсы:
https://ru.wikipedia.org
http://www.krugosvet.ru
http://festival.1september.ru
http://school-assistant.ru/?class=7_algebra
http://www.openclass.ru
http://www.physics.ru
http://www.physbook.ru
http://120na80-norma.com/polezno-znat/davlenie-cheloveka-norma-po-vozrastu.html.









 амо слово «функция» (от латинского functio – совершение, выполнение) впервые было употреблено немецким математиком Лейбницем (1646–1716) в 1673 г. в письме к Х. Гюйгенсу (1629–1695) (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону), а в печати введено с 1694 года. Начиная с 1698 года, Лейбниц ввел также термины «переменная» и «константа».
амо слово «функция» (от латинского functio – совершение, выполнение) впервые было употреблено немецким математиком Лейбницем (1646–1716) в 1673 г. в письме к Х. Гюйгенсу (1629–1695) (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону), а в печати введено с 1694 года. Начиная с 1698 года, Лейбниц ввел также термины «переменная» и «константа».  кончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Леонард Эйлер. «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств». Так понимали функцию на протяжении почти всего 18 века французские математики Жан Лерон Даламбер (1717–1783), Жозеф Луи Лагранж (1736–1813), Жан Батист Жозеф Фурье (1768–1830) и другие видные математики.
кончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Леонард Эйлер. «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств». Так понимали функцию на протяжении почти всего 18 века французские математики Жан Лерон Даламбер (1717–1783), Жозеф Луи Лагранж (1736–1813), Жан Батист Жозеф Фурье (1768–1830) и другие видные математики.



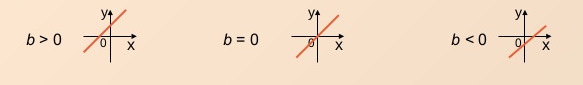 При k 0, прямая образует острый угол с осью абсцисс:
При k 0, прямая образует острый угол с осью абсцисс: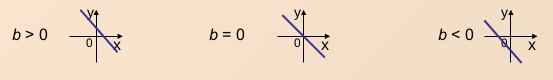 При k
При k 













