Муниципальное казенное общеобразовательное учреждение
Васильевская основная общеобразовательная школа
Бутурлиновского района Воронежской области
«Согласовано»
Руководитель ШМО
_______/ /
Протокол № __
От «__» __________ 201 г.
«Согласовано»:
Заместитель руководителя по УР
МКОУ Васильевская ООШ
________ /Моргунова И. Н./
«__» _____________ 201 г.
«Утверждаю»:
Директор МКОУ Васильевская ООШ
__________/Дегтярёв Н. М./
Приказ № ____
от «__» _________ 201 г.
Рабочая программа
учебного предмета
«Математика»
8 класс
Разработана
Моргуновой Ириной Николаевной
учителем математики
первой квалификационной категории
2016 – 2017 учебный год.
РАБОЧАЯ ПРОГРАММА
Рабочая программа по математике для основной общеобразовательной школы составлена на основе следующих нормативно-правовых и инструктивно-методических документов:
приказ МО РФ Приказ МО РФ №1089 от 05.03.2004 г «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования»;
программы общеобразовательных учреждений. Геометрия. 7 – 9 классы / Т.А.Бурмистрова. – М.: Просвещение, 2011;
программы общеобразовательных учреждений. Алгебра 7 – 9 классы / Т.А.Бурмистрова. – М.: Просвещение, 2011.
Рабочая программа включает три раздела: пояснительную записку, требования к результатам освоения курса математики основной школы, содержание курса по основным линиям. К программе прилагаются примерное тематическое планирование с указанием примерного числа часов на изучение соответствующего материала и описанием формируемых компетенций учащихся и календарно-тематическое планирование учебного материала.
Рабочая программа выполняет две основные функции.
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Общая характеристика учебного предмета
Математическое образование в основной школе складывается из следующих содержательных компонентов: арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно ёмком и значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчёркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов, для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Геометрия – один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Элементы комбинаторики, теории вероятностей, статистики и логики становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
Таким образом, в ходе освоения содержания курса учащиеся получают возможность:
развить представление о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Цели
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как части общечеловеческой культуры, играющей особую роль в общественном развитии.
Общеучебные умения, навыки и способы деятельности
В ходе преподавания математики в основной школе, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общенаучного характера, разнообразными способами деятельности, приобретали опыт:
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Место предмета в федеральном базисном учебном плане
Согласно федеральному базисному учебному плану для общеобразовательных учреждений Российской Федерации на изучение математики в 8 классе отводится не менее 175 часов (из расчёта 5 часов в неделю).
Рабочая программа рассчитана на 175 учебных часа. На преподавание курса алгебры – 3 часа в неделю всего 105 часов, из них контрольных работ 10 часов. На преподавание курса геометрии – 2 часа в неделю всего 70 часов, из них контрольных работ 6 часов.
Результаты обучения
Результаты обучения представлены в Требованиях к результатам обучения и освоения курса математики основной школы и задают систему итоговых результатов обучения, достижение которых является обязательным условием положительной аттестации ученика за курс основной школы. Требования распределены по основным содержательным линиям курса и характеризуют тот безусловный минимум, которого должны достигать все учащиеся.
Содержание обучения (алгебра, 8 класс)
1. Рациональные дроби.
Рациональная дробь. Основное свойство дроби, сокращение дробей. Тождественные преобразования рациональных выражений.
Функция  и ее график.
и ее график.
Основная цель: выработать умение выполнять тождественные преобразования рациональных выражений.
Так как действия с рациональными дробями существенным образом опираются на действия с многочленами, то в начале темы необходимо повторить с учащимися преобразования целых выражений.
Главное место в данной теме занимают алгоритмы действий с дробями. Учащиеся должны понимать, что сумму, разность, произведение и частное дробей всегда можно представить в виде дроби. Приобретаемые в данной теме умения выполнять сложение, вычитание, умножение и деление дробей являются опорными в преобразованиях дробных выражений. Поэтому им следует уделить особое внимание. Нецелесообразно переходить к комбинированным заданиям на все действия с дробями прежде, чем будут усвоены основные алгоритмы. Задания на все действия с дробями не должны быть излишне громоздкими и трудоемкими.
При нахождении значений дробей даются задания на вычисления с помощью калькулятора. В данной теме расширяются сведения о статистических характеристиках. Вводится понятие среднего гармонического ряда положительных чисел.
Изучение темы завершается рассмотрением свойств графика функции  .
.
2. Квадратные корни.
Понятие об иррациональных числах. Общие сведения о действительных числах. Квадратный корень. Понятие о нахождении приближенного значения квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция  ее свойства и график.
ее свойства и график.
Основная цель: систематизировать сведения о рациональных числах и дать представление об иррациональных числах, расширив тем самым понятие о числе; выработать умение выполнять преобразования выражений, содержащих квадратные корни.
В данной теме учащиеся получают начальное представление о понятии действительного числа. С этой целью обобщаются известные учащимся сведения о рациональных числах. Для введения понятия иррационального числа используется интуитивное представление о том, что каждый отрезок имеет длину и потому каждой точке координатной прямой соответствует некоторое число. Показывается, что существуют точки, не имеющие рациональных абсцисс.
При введении понятия корня полезно ознакомить учащихся с нахождением корней с помощью калькулятора.
Основное внимание уделяется понятию арифметического квадратного корня и свойствам арифметических квадратных корней. Доказываются теоремы о корне из произведения и дроби, а также тождество 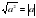 , которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида
, которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида 
 . Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
. Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
Продолжается работа по развитию функциональных представлений учащихся. Рассматриваются функция  , ее свойства и график. При изучении функции
, ее свойства и график. При изучении функции  показывается ее взаимосвязь с функцией
показывается ее взаимосвязь с функцией  , где x ≥ 0.
, где x ≥ 0.
3. Квадратные уравнения.
Квадратное уравнение. Формула корней квадратного уравнения. Решение рациональных уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям.
Основная цель: выработать умения решать квадратные уравнения и простейшие рациональные уравнения и применять их к решению задач.
В начале темы приводятся примеры решения неполных квадратных уравнений. Этот материал систематизируется. Рассматриваются алгоритмы решения неполных квадратных уравнений различного вида.
Основное внимание следует уделить решению уравнений вида ах2 + bх + с = 0, где а ≠ 0, с использованием формулы корней. В данной теме учащиеся знакомятся с формулами Виета, выражающими связь между корнями квадратного уравнения и его коэффициентами. Они используются в дальнейшем при доказательстве теоремы о разложении квадратного трехчлена на линейные множители.
Учащиеся овладевают способом решения дробных рациональных уравнений, который состоит в том, что решение таких уравнений сводится к решению соответствующих целых уравнений с последующим исключением посторонних корней.
Изучение данной темы позволяет существенно расширить аппарат уравнений, используемых для решения текстовых задач.
4. Неравенства.
Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Погрешность и точность приближения. Линейные неравенства с одной переменной и их системы.
Основная цель: ознакомить учащихся с применением неравенств для оценки значений выражений, выработать умение решать линейные неравенства с одной переменной и их системы.
Свойства числовых неравенств составляют ту базу, на которой основано решение линейных неравенств с одной переменной. Теоремы о почленном сложении и умножении неравенств находят применение при выполнении простейших упражнений на оценку выражений по методу границ. Вводятся понятия абсолютной погрешности и точности приближения, относительной погрешности.
Умения проводить дедуктивные рассуждения получают развитие как при доказательствах указанных теорем, так и при выполнении упражнений на доказательства неравенств.
В связи с решением линейных неравенств с одной переменной дается понятие о числовых промежутках, вводятся соответствующие названия и обозначения. Рассмотрению систем неравенств с одной переменной предшествует ознакомление учащихся с понятиями пересечения и объединения множеств.
При решении неравенств используются свойства равносильных неравенств, которые разъясняются на конкретных примерах. Особое внимание следует уделить отработке умения решать простейшие неравенства вида ахb, ахb, остановившись специально на случае, когда а0.
В этой теме рассматривается также решение систем двух линейных неравенств с одной переменной, в частности таких, которые записаны в виде двойных неравенств.
5. Степень с целым показателем. Элементы статистики.
Степень с целым показателем и её свойства. Стандартный вид числа. Начальные сведения об организации статистических исследований.
Основная цель: выработать умение применять свойства степени с целым показателем в вычислениях и преобразованиях, сформировать начальные представления о сборе и группировке статистических данных, их наглядной интерпретации.
В этой теме формулируются свойства степени с целым показателем. Метод доказательства этих свойств показывается на примере умножения степеней с одинаковыми основаниями. Дается понятие о записи числа в стандартном виде. Приводятся примеры использования такой записи в физике, технике и других областях знаний.
Учащиеся получают начальные представления об организации статистических исследований. Они знакомятся с понятиями генеральной и выборочной совокупности. Приводятся примеры представления статистических данных в виде таблиц частот и относительных частот. Учащимся предлагаются задания на нахождение по таблице частот таких статистических характеристик, как среднее арифметическое, размах и мода. Рассматривается вопрос о наглядной интерпретации статистической информации. Известные учащимся способы наглядного представления статистических данных с помощью столбчатых и круговых диаграмм расширяются за счёт введения таких понятий, как полигон и гистограмма.
6. Повторение.
Основная цель: повторение, обобщение и систематизация знаний, умений и навыков за курс алгебры 8 класса.
Содержание обучения (геометрия, 8 класс)
1. Четырёхугольники.
Определение четырехугольника. Параллелограмм и его свойства Признаки параллелограмма. Прямоугольник, ромб, квадрат и их свойства. Теорема Фалеса. Средняя линия треугольника. Трапеция. Средняя линия трапеции. Пропорциональные отрезки.
Основная цель: дать учащимся систематизированные сведения о четырехугольниках и их свойствах.
Доказательства большинства теорем данной темы проводятся с опорой на признаки равенства треугольников, которые используются и при решении задач в совокупности с применением новых теоретических фактов. Поэтому изучение темы можно организовать как процесс обобщения и систематизации знаний учащихся о свойствах треугольников, осуществив перенос усвоенных методов на новый объект изучения.
Вводимые при изучении темы сведения о различных видах четырехугольников и их свойствах играют важную роль в изучении последующего материала. Основное внимание следует направить на решения задач, в ходе которых отрабатываются практические умения применять свойства и признаки параллелограмма и его частных видов, необходимые для распознавания конкретных видов четырехугольников и вычисления их элементов.
Рассматриваемая в теме теорема Фалеса (теорема о пропорциональных отрезках) играет вспомогательную роль в построении курса. Воспроизведения ее доказательства необязательно требовать от учащихся. Примером применения теоремы Фалеса является доказательство теоремы о средней линии треугольника. Теорема о пропорциональных отрезках используется в доказательстве теоремы о косинусе угла прямоугольного треугольника.
2. Теорема Пифагора.
Синус, косинус и тангенс острого угла прямоугольного треугольника. Теорема Пифагора. Неравенство треугольника. Перпендикуляр и наклонная. Соотношение между сторонами и углами в прямоугольном треугольнике. Значения синуса, косинуса и тангенса некоторых углов.
Основная цель: сформировать аппарат решения прямоугольных треугольников, необходимый для вычисления элементов геометрических фигур на плоскости и в пространстве.
Изучение теоремы Пифагора позволяет существенно расширить круг геометрических задач, давая вместе с признаками равенства треугольников достаточно мощный аппарат решения задач.
Большое внимание в данной теме уделяется вопросам, связанным с решением прямоугольных треугольников. Для этого необходимо прочное усвоение определений синуса, косинуса и тангенса острого угла,
В ходе решения задач усваиваются основные алгоритмы решения прямоугольных треугольников, при проведении практических вычислений вырабатываются навыки нахождения с помощью таблиц или калькуляторов значений синуса, косинуса и тангенса угла, а в ряде задач используются значения синуса, косинуса и тангенса углов 30°, 45 , 60°.
Соответствующие умения являются опорными для решения вычислительных задач и доказательств ряда теорем в курсе планиметр и pi и стереометрии. Кроме того, они используются и в курсе физики. Поэтому необходимо добиться прочных навыков практического применения этих фактов в решении вычислительных задач. При изучении данной темы широко используются и получают дальнейшее развитие такие навыки и алгебраические умения учащихся, как решение квадратных уравнений, извлечение квадратных корней, преобразования алгебраических уравнений.
В конце темы рассматривается теорема о неравенстве треугольника. Тем самым пополняются знания учащихся о свойствах расстояний между точками. Наиболее важным с практической точки зрения является случай, когда данные точки не лежат на одной прямой, т. е. свойство сторон треугольника. Его полезно закрепить на ряде примеров. В то же время воспроизведения доказательства теоремы можно от учащихся не требовать.
3. Декартовы координаты на плоскости.
Прямоугольная система координат на плоскости. Координаты середины отрезка. Расстояние между точками. Уравнения прямой и окружности. Координаты точки пересечения прямых. График линейной функции. Пересечение прямой с окружностью. Синус, косинус и тангенс углов от 0° до 180°.
Основная цель: обобщить и систематизировать представления учащихся о декартовых координатах; развить умение применять алгебраический аппарат при решении геометрических задач.
В начале темы вводится определение декартовых координат, выводятся формулы для нахождения координаты середины отрезка и расстояния между точками. Рассматриваются уравнения окружности и прямой и способы нахождения с их помощью координат точки пересечения прямых, прямой с окружностью.
В данной теме демонстрируется эффективность применения формул для координат середины отрезка, расстояния между точками, уравнений окружности и прямой в конкретных геометрических задачах, тем самым дается представление об изучении геометрических фигур с помощью методов алгебры.
4. Движение.
Движение и его свойства. Симметрия относительно точки и прямой. Поворот. Параллельный перенос и его свойства. Понятие о равенстве фигур.
Основная цель: познакомить учащихся с примерами геометрических преобразований.
Поскольку в дальнейшем движения не применяются в качестве аппарата для решения задач и изложения теории, можно рекомендовать изучение материала в ознакомительном порядке, т.е. не требовать от учащихся воспроизведения доказательств, Однако основные понятия — симметрия относительно точки и прямой, параллельный перенос — учащиеся должны усвоить на уровне практических применений.
5. Векторы.
Вектор. Абсолютная величина и направление вектора. Равенство векторов. Координаты вектора. Сложение векторов и его свойства. Умножение вектора на число. [Коллинеарные векторы.] Скалярное произведение векторов. Угол между векторами. [Проекция на ось. Разложение вектора по координатным осям.]
Основная цель: познакомить учащихся с элементами векторной алгебры и их применением для решения геометрических задач; сформировать умение производить операции над векторами.
Основное внимание следует уделить формированию практических умений учащихся, связанных с вычислением координат вектора, его абсолютной величины, выполнением сложения и вычитания векторов, умножения вектора на число. Наряду с операциями над векторами в координатной форме следует уделить большое внимание операциям в геометрической форме. Действия над векторами в координатной и геометрической формах используются при параллельном изучении курса физики. Знания о векторных величинах, приобретенные на уроках физики, могут быть использованы для мотивированного введения на предметной основе ряда основных понятий темы.
6. Повторение. Решение задач.
Основная цель: повторение, обобщение и систематизация знаний, умений и навыков за курс геометрии 8 класса.
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ (алгебра, 8 класс)
3 ч в неделю, всего 105 ч
| № п/п | Содержание материала
| Количество часов |
| Рациональные дроби | 23 |
| 1 2 3
4 5 | Рациональные дроби и их свойства Сумма и разность дробей Контрольная работа по теме «Сложение и вычитание дробей». Произведение и частное дробей Контрольная работа по теме «Преобразование рациональных выражений». | 3 8 1
10 1 |
| Квадратные корни | 17 |
| 6 7 8 9 10
11 | Действительные числа Арифметический квадратный корень Свойства арифметического квадратного корня Контрольная работа по теме «Квадратный корень». Применение свойств арифметического квадратного корня Контрольная работа по теме «Преобразование выражений, содержащих квадратные корни». | 2 3 6 1 4
1 |
| Квадратные уравнения | 22 |
| 12 13
14 15 | Квадратное уравнение и его корни Контрольная работа по теме «Квадратные уравнения». Дробные рациональные уравнения Контрольная работа по теме «Дробные рациональные уравнения». | 10 1
10 1 |
| Неравенства | 18 |
| 16 17
18 19 | Числовые неравенства и их свойства Контрольная работа по теме «Числовые неравенства». Неравенства с одной переменной и их системы Контрольная работа по теме «Системы неравенств с одной переменной» | 7 1
9 1 |
| Степень с целым показателем. Элементы статистики | 12 |
| 20 21 22
| Степень с целым показателем и ее свойства. Элементы статистики. Контрольная работа по теме «Степень с целым показателем».
| 6 5 1 |
| Повторение
| 12 |
|
| Итоговая контрольная работа | 1 |
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ (геометрия, 8 класс)
2 ч в неделю, всего 70 ч
| № п/п | Содержание материала | Кол-во часов |
| Четырёхугольники | 19 |
| 1 2 3 4 5 6 7 | Урок вводного повторения. Определение четырёхугольника. Параллелограмм. Прямоугольник. Ромб. Квадрат. Контрольная работа по теме «Четырёхугольники». Теорема Фалеса. Средняя линия треугольника. Трапеция. Контрольная работа по теме «Трапеция».
| 1 5 5 1 3 3 1 |
| Теорема Пифагора | 15 |
| 8 9 10
11
12
13 | Косинус угла. Теорема Пифагора. Египетский треугольник. Контрольная работа по теме «Теорема Пифагора». Соотношение между сторонами и углами в прямоугольном треугольнике. Основные тригонометрические тождества. Значения синуса, косинуса и тангенса некоторых углов. Изменение синуса, косинуса и тангенса при возрастании угла. Контрольная работа по теме «Тригонометрические функции». | 5 1 3
3
2
1
|
| Декартовы координаты на плоскости | 18 |
| 14
15
16
17
18 | Определение декартовых координат. Координаты середины отрезка. Расстояние между точками. Уравнение окружности. Уравнение прямой. Координаты точки пересечения прямых. Расположение прямой относительно системы координат. Угловой коэффициент в уравнении прямой. График линейной функции. Пересечение прямой с окружностью. Определение синуса, косинуса и тангенса любого угла от 0° до 180°. Контрольная работа по теме «Декартовы координаты на плоскости». | 4
4
4
5
1
|
| Движение | 6 |
| 19 20 | Преобразование фигур. Свойства движения. Симметрия. Параллельный перенос. Поворот.
| 3 3 |
| Векторы | 8 |
| 21 22 | Векторы. Итоговая контрольная работа. | 7 1 |
| Итоговое повторение | 3 |
Календарно-тематическое планирование уроков алгебры 8 класса.
| Номер урока | Содержание учебного материала. | Количество часов | Дата |
| Глава I. Рациональные дроби и их свойства. |
| 1-3 | Повторение. Рациональные выражения. | 3 |
|
| 4-6 | Основное свойство дроби. Сокращение дробей. | 3 |
|
| 7-8 | Сложение и вычитание дробей с одинаковыми знаменателями. | 2 |
|
| 9-11 | Сложение и вычитание дробей с разными знаменателями. | 3 |
|
| 12 | Контрольная работа № 1. | 1 |
|
| 13-14 | Умножение дробей. Возведение дроби в степень. | 2 |
|
| 15-16 | Деление дробей. | 2 |
|
| 17-20 | Преобразование рациональных выражений. | 4 |
|
| 21-22 | Функция и её график. | 2 |
|
| 23 | Контрольная работа № 2. | 1 |
|
| ГлаваII. Квадратные корни. |
| 24-25 | Рациональные и иррациональные числа. | 2 |
|
| 26-27 | Квадратные корни. Арифметический квадратный корень. | 2 |
|
| 28 | Уравнение х2=а. | 1 |
|
| 29 | Нахождение приближённых значений квадратного корня. | 1 |
|
| 30-31 | Функция у=√х и её график. | 2 |
|
| 32-34 | Квадратный корень из произведения, дроби, степени. | 3 |
|
| 35 | Контрольная работа № 3. | 1 |
|
| 36-37 | Вынесение множителя из-под знака корня. Внесение множителя под знак корня. | 2 |
|
| 38-39 | Преобразование выражений, содержащих квадратные корни. | 2 |
|
| 40 | Контрольная работа № 4. | 1 |
|
| Глава III. Квадратные уравнения. |
| 41-42 | Определение квадратного уравнения. Неполные квадратные уравнения. | 2 |
|
| 43 | Решение квадратных уравнений выделением квадрата двучлена. | 1 |
|
| 44-46 | Решение квадратных уравнений по формуле. | 3 |
|
| 47-48 | Решение задач с помощью квадратных уравнений. | 2 |
|
| 49-50 | Теорема Виета. | 2 |
|
| 51 | Контрольная работа № 5. | 1 |
|
| 52-55 | Решение дробных рациональных уравнений. | 4 |
|
| 56-59 | Решение задач с помощью дробных рациональных уравнений. | 4 |
|
| 60-61 | Графический способ решения уравнений. | 2 |
|
| 62 | Контрольная работа № 6. | 1 |
|
| Глава IV. Неравенства. |
| 63-66 | Числовые неравенства. Свойства числовых неравенств. | 4 |
|
| 67-69 | Сложение и умножение числовых неравенств. | 3 |
|
| 70 | Контрольная работа № 7. | 1 |
|
| 71-72
| Числовые промежутки. | 2 |
|
| 73-76 | Решение неравенств с одной переменной. | 4 |
|
| 77-78 | Решение систем неравенств с одной переменной. | 2 |
|
| 79 | Решение систем неравенств с одной переменной (продолжение). | 1 |
|
| 80 | Контрольная работа № 8. | 1 |
|
| Глава V. Степень с целым показателем. |
| 81-82 | Определение степени с целым отрицательным показателем. | 2 |
|
| 83-84 | Свойства степени с целым показателем. | 2 |
|
| 85-86 | Стандартный вид числа. | 2 |
|
| 87-88 | Сбор и группировка статистических данных. | 2 |
|
| 89-91 | Наглядное представление статистической информации. | 3 |
|
| 92 | Контрольная работа № 9. | 1 |
|
| 93-104 | Итоговое повторение курса алгебры 8 класса. Решение задач. | 12 |
|
| 105 | Итоговая контрольная работа № 10. | 1 |
|
Календарно-тематическое планирование уроков геометрии 8 класса.
| Номер урока | Содержание учебного материала | Количество часов | Дата |
| I четверть. 2 урока в неделю, 18 уроков за четверть. |
| 1 | Урок вводного повторения | 1 |
|
| Глава VI. Четырёхугольники (19 часов). |
| 2 - 3 | Определение четырёхугольника. | 2 |
|
| 4 - 6 | Параллелограмм. | 3 |
|
| 7 - 11 | Прямоугольник, ромб, квадрат. | 5 |
|
| 12 | Контрольная работа № 1. | 1 |
|
| 13 -15 | Теорема Фалеса. | 3 |
|
| 16 - 18 | Трапеция. | 3 |
|
| II четверть. 2 урока в неделю, 16 уроков за неделю. |
| 19-20 | Трапеция. | 2 |
|
| 21 | Контрольная работа № 2. | 1 |
|
| Глава VII. Теорема Пифагора (16 часов). |
| 22 - 23 | Косинус угла. | 2 |
|
| 24 - 26 | Теорема Пифагора. | 3 |
|
| 27 | Контрольная работа № 3. | 1 |
|
| 28 - 29 | Соотношение между сторонами и углами в прямоугольном треугольнике. | 2 |
|
| 30 | Как пользоваться таблицами синусов, косинусов, тангенсов. | 1 |
|
| 31 | Основные тригонометрические тождества. | 1 |
|
| 32 - 33 | Значение синуса, косинуса и тангенса некоторых углов. | 2 |
|
| 34 | Измерение синуса, косинуса и тангенса при возрастании угла. | 1 |
|
| III четверть. 2 урока в неделю, 20 уроков за четверть. |
| 35 | Измерение синуса, косинуса и тангенса при возрастании угла. | 1 |
|
| 36 | Контрольная работа № 4. | 1 |
|
| Глава VIII. Декартовы координаты на плоскости. |
| 37 | Введение координат на плоскости. | 1 |
|
| 38 | Координаты середины отрезка. | 1 |
|
| 39 - 40 | Расстояние между точками. | 2 |
|
| 41 - 43 | Уравнение окружности. | 3 |
|
| 44 | Уравнение прямой. | 1 |
|
| 45 - 46 | Расположение прямой относительно системы координат. | 2 |
|
| 47 - 48 | Пересечение прямой с окружностью. | 2 |
|
| 49 - 53 | Определение синуса, косинуса и тангенса для любого угла от 00 до 1800. | 5 |
|
| 54 | Контрольная работа № 5. | 1 |
|
| IV четверть. 2 урока в неделю, 16 уроков за четверть. |
| 55 | Примеры преобразования фигур. | 1 |
|
| 56 -57 | Свойства движения. | 2 |
|
| 58 - 59 | Параллельный перенос и его свойства. | 2 |
|
| 60 | Понятие вектора. Равенство векторов. | 1 |
|
| 61 | Откладывание вектора от данной точки. | 1 |
|
| 62 - 64 | Сложение и вычитание векторов. | 3 |
|
| 65 | Умножение вектора на число. | 1 |
|
| 66 | Скалярное произведение векторов. | 1 |
|
| 67 | Контрольная работа № 6. | 1 |
|
| 68 - 70 | Повторение. | 3 |
|
Учебно-методическое обеспечение.
Федеральный компонент государственных образовательных стандартов основного общего образования (приказ Минобрнауки от 05.03.2004г. № 1089).
Временные требования к минимуму содержания основного общего образования (утверждены приказом МО РФ от 19.05.98 № 1236).
Примерная программа по математике (письмо Департамента государственной политики в образовании Минобрнауки России от 07.07.2005г № 03-1263).
Примерная программа для общеобразовательных школ, гимназий, лицеев по математике 5-11 классы к учебному комплексу для 7-9 классов (авторы Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков, С.Б. Суворова Ю.Н., составители Г.М. Кузнецова, Н.Г. Миндюк– М: «Дрофа», 2004. – с. 86-91)
Оценка качества подготовки выпускников основной школы по математике/ Г.В.Дорофеев и др.– М.: Дрофа, 2000.
Алгебра-9:учебник/автор: Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков, С.Б. Суворова, Просвещение, 2004 – 2007 год.
Изучение алгебры в 7—9 классах/ Ю. Н. Макарычев, Н. Г. Миндюк, С. Б. Суворова..— М.: Просвещение, 2005—2008.
Уроки алгебры в 9 классе: кн. для учителя / В. И. Жохов, Л. Б. Крайнева. — М.: Просвещение, 2005— 2008.
Алгебра: дидакт. материалы для 9 кл. / Л. И. Звавич, Л. В. Кузнецова, С. Б» Суворова. — М.: Просвещение, 2007—2008.
Элементы статистики и теории вероятностей: Учеб пособие для обучающихся 7-9 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк; под ред. С.А. Теляковского. –– М.: Просвещение,2001 -2007г.
Математика 5-11 классы: нетрадиционные формы организации контроля на уроках / авт.-сост. М.Е. Козина, О.М. Фадеева. - Волгоград, Учитель, 2007;
В.И.Жохов, Л.Б.Крайнева Уроки алгебры в 9 классе- М.: «Вербум - М», 2000;
Н.П.Кострикина Задачи повышенной трудности в курсе алгебры 7-9 классов - М : Просвещение», 1991;
Нестандартные уроки алгебры. 8 класс. Сост. Ким Н.А. – Волгоград: ИТД «Корифей», 2006;
А.Г. Мордкович, П.В.Семенов События. Вероятности. Статистическая обработка данных. 7-9 классы. – М.: «Мнемозина»,2003;
Перечень сайтов
http://www.prosv.ru - сайт издательства «Просвещение» (рубрика «Математика»)
http:/www.drofa.ru - сайт издательства Дрофа (рубрика «Математика»)
http://www.center.fio.ru/som - методические рекомендации учителю-предметнику (представлены все школьные предметы). Материалы для самостоятельной разработки профильных проб и активизации процесса обучения в старшей школе.
http://www.edu.ru - Центральный образовательный портал, содержит нормативные документы Министерства, стандарты, информацию о проведение эксперимента, сервер информационной поддержки Единого государственного экзамена.
http://www.internet-scool.ru - сайт Интернет – школы издательства Просвещение. Учебный план разработан на основе федерального базисного учебного плана для общеобразовательных учреждений РФ и представляет область знаний «Математика». На сайте представлены Интернет-уроки по алгебре и началам анализа и геометрии, включают подготовку сдачи ЕГЭ, ГИА.
http://www.legion.ru – сайт издательства «Легион»
http://www.intellectcentre.ru – сайт издательства «Интеллект-Центр», где можно найти учебно-тренировочные материалы, демонстрационные версии, банк тренировочных заданий с ответами, методические рекомендации и образцы решений
http://www.fipi.ru - портал информационной поддержки мониторинга качества образования, здесь можно найти Федеральный банк тестовых заданий.







 и ее график.
и ее график. .
. ее свойства и график.
ее свойства и график.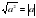 , которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида
, которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида 
 . Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
. Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа. , где x ≥ 0.
, где x ≥ 0.









