Рабочая программа по математике 10-11 класс

Муниципальное казенное общеобразовательное учреждение

А-Донская средняя общеобразовательная школа

Павловского муниципального района

Воронежской области

«ПРИНЯТО» «УТВЕРЖДАЮ»

на заседании педагогического совета Директор МКОУ А-Донская СОШ

Протокол № ___от ______ 202__ ___________ С.А.Тертышникова

Приказ № ____ от _____202__

Согласовано с Советом школы

Протокол №___ от ___202_

РАБОЧАЯ ПРОГРАММА

Учебный предмет - математика

Классы - 10-11

Уровень образования: среднее общее образование

Срок реализации программы – 2 года

Программа разработана учителем математики Антощенко О.Л.

в соответствии с Федеральным государственным образовательным стандартом основного общего образования (ФГОС) и основной образовательной программой основного общего образования МКОУ А-Донская СОШ

Александровка Донская

2021 г.

Пояснительная записка

Рабочая программа составлена на основе:

1. Федерального закона "Об образовании в Российской Федерации" от 29.12.2012 N 273-ФЗ

2.Приказа Министерства образования и науки Российской Федерации №1897 от 17 октября 2010 г. «Об утверждении и введении в действие федерального государственного стандарта основного общего образования» ( в редакции от 29.12.2014 г.№1644, от 31.12.2015г.№1577, от 07.06.2017 года №506)

3.Приказа Министерства образования и науки Российской Федерации от 08.05.2019 года № 233 « О внесении изменений в федеральный перечень учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования, утвержденный приказом Министерства просвещения Российской Федерации от 28.12.2018 года № 345.

4.Перечня организаций, осуществляющих выпуск учебных пособий, которые допускаются к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования, утвержденного приказом Министерства образования и науки Российской Федерации от 09.06.2016 №699

5. Постановления Главного государственного санитарного врача РФ от 28 сентября 2020 г. №28 «Об утверждении санитарных правил СП 2.4.3648-20 "Санитарно-эпидемиологические требования к организациям воспитания и обучения, отдыха и оздоровления детей и молодежи".

6. Постановления Главного государственного санитарного врача РФ от 28.01.2021 г. № 2 "Об утверждении санитарных правил и норм СанПиН 1.2.3685-21 "Гигиенические нормативы и требования к обеспечению безопасности и (или) безвредности для человека факторов среды обитания"

7.Приказа Mинздравсоцразвития России от 26.08.2010 № 761н (ред. от 31.05.2011) «Об утверждении Единого квалификационного справочника должностей руководителей, специалистов и служащих, раздел «Квалификационные характеристики должностей работников образования»» (Зарегистрировано в Минюсте РФ 06.10.2010 N 18638).

8.Порядка организации и осуществления образовательной деятельности по основным общеобразовательным программам – образовательным программам начального общего, основного общего и среднего общего образования, утвержденный приказом Министерства образования и науки Российской Федерации от 30.08.2013 № 1015 (с изменениями и дополнениями от: 13.12.2013 г., 28.05 2014 г., 17.07 2015 г.);

9.Письма министерства образования и науки РФ от 18.06.2015 г. № НТ-670/08 «Методические рекомендации по организации самоподготовки учащихся при осуществлении образовательной деятельности по основным образовательным программам- образовательным программам начального общего, основного общего и среднего общего образования»

10. На основании Устава школы;

11.На основании учебного плана МКОУ А-Донская СОШ

12. На основании примерной программы по математике среднего общего образования «Программы общеобразовательных учреждений Математиа 10-11 классы» /составитель Т.А.Бурмистрова/,М.: издательство «Просвещение», 2011г

Программа по алгебре и началам анализа и геометрии составлена на основе Федерального государственного стандарта с учетом Концепции математического образования и Фундаментального ядра содержания общего образования, требований к результатам освоения образовательной программы среднего общего образования, представленных в федеральном государственном стандарте среднего общего образования с учётом преемственности с Примерными программами для основного общего образования по математике. В ней также учитываются доминирующие идеи и положения Программы развития и формирования универсальных учебных действий для основного общего образования, которые обеспечивают формирование российской гражданской идентичности, коммуникативных качеств личности, и способствуют формированию ключевой компетенции – умению учиться.

Программа по математике направлена на реализацию системно – деятельностного подхода к процессу обучения, который обеспечивает:

построение образовательного процесса с учётом индивидуальных возрастных, психологических, физиологических особенностей и здоровья обучающихся;

формирование готовности обучающихся к саморазвитию и непрерывному образованию;

формирование активной учебно-познавательной деятельности обучающихся;

формирование позитивного отношения к познанию научной картины мира;

осознанную организацию обучающимися своей деятельности, а также адекватное её оценивание;

построение развивающей образовательной среды обучения.

Математическое образование является обязательной и неотъемлемой частью общего образования. Обучение математике в основной школе направлено на достижение следующих целей:

I

В направлении личностного развития:

• воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;

• ответственное отношение к учению, готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;

• осознанный выбор и построение дальнейшей индивидуальной траектории образования на базе ориентировки

• в мире профессий и профессиональных предпочтений с учётом устойчивых познавательных интересов, а также на основе формирования уважительного отношения к труду, развитие опыта участия в социально значимом труде;

• умение контролировать процесс и результат учебной и математической деятельности;

• критичность мышления, инициатива, находчивость, активность при решении математических задач.

В метапредметном направлении:

• приобретение опыта осуществления учебно-исследовательской, проектной и информационно-познавательной деятельности;

• формирование общих способов интеллектуальной деятельности, характер­ных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;

• приобретение опыта осуществления учебно-исследовательской, проектной и информационно-познавательной деятельности.

В предметном направлении:

• развитие интереса обучающихся к изучению алгебры и начал математического анализа и геометрии;

• использование математических моделей для решения прикладных задач, задач из смежных дисциплин.

Задачи:

• овладеть системой математических знаний и умений, необходимых для применения в практической деятельности, изучении смежных дисциплин;

• способствовать интеллектуальному развитию, формировать качества, необходимые человеку для полноценной жизни в современном обществе, свойственные математической деятельности: ясности и точности мысли, интуиции, логического мышления, пространственных представлений, способности к преодолению трудностей;

• формировать представления об идеях и методах математики как универсального языка науки и техники, средствах моделирования явлений и процессов;

• воспитывать культуру личности, отношение к математике как части общечеловеческой культуры, играющей особую роль в общественном развитии.

Общая характеристика учебного предмета

Содержание курса алгебры и начал математического анализа в 10 – 11 классах представлено в виде следующих содержательных разделов: числа и величины, выражения, уравнения и неравенства, функции, элементы математического анализа, вероятность и статистика. Работа с данными, алгебра и начала математического анализа в историческом развитии.

В разделе «Числа и величина» расширяется понятие числа, которое служит фундаментом гибкого и мощного аппарата, используемого в решении математических задач и в решении задач смежных дисциплин. Материал данного раздела завершает содержательную линию школьного курса математики «Числа и величины».

Особенностью раздела «Выражения» является то, что материал изучается в разных темах курса: «Показательная и логарифмическая функции», «Тригонометрические функции», «Степенная функция». При изучении этого раздела формируется представление о прикладном значении математики, о первоначальных принципах вычислительной математики. В задачи изучения раздела входит развитие умения решать задачи рациональными методами, вносить необходимые коррективы в ходе решения задачи.

Особенностью раздела «Уравнения и неравенства» является то, что материал изучается в разных темах курса: «Показательная и логарифмическая функции», «Тригонометрические функции», «Степенная функция». Материал данного раздела носит прикладной характер и учитывает взаимосвязь системы научных знаний и метода познания — математического моделирования, представляет широкие возможности для развития алгоритмического мышления, обеспечивает опыт продуктивной деятельности для развития мотивации к обучению и интеллекта.

Раздел «Функции» расширяет круг элементарных функций, изученных в курсе алгебры 7—9 классов, а также методов их исследования. Целью изучения данного раздела является формирование умения соотносить реальные зависимости из окружающей жизни и из смежных дисциплин с элементарными функциями, использовать функциональные представления для решения задач. Соответствующий материал способствует развитию самостоятельности в организации и проведении исследований, воображения и творческих способностей учащихся.

Материал раздела «Элементы математического анализа», включающий в себя темы «Производная и её применение» и «Интеграл и его применение», формирует представления об общих идеях и методах математического анализа. Цель изучения раздела — применение аппарата математического анализа для решения математических и практических задач, а также для доказательства ряда теорем математического анализа и геометрии.

Содержание раздела «Вероятность и статистика. Работа с данными» раскрывает прикладное и практическое значение математики в современном мире. Материал данного раздела способствует формированию умения воспринимать, представлять и критически анализировать информацию, представленную в различных формах, пониманию вероятностного характера реальных зависимостей.

Раздел «Алгебра и начала математического анализа в историческом развитии» позволяет сформировать представление о культурных и исторических факторах становления математики как науки, о ценности математических знаний и их применении в современном мире, о связи научного знания и ценностных установок.

Содержание курса геометрии в 10—11 классах представлено в виде следующих содержательных разделов: «Параллельность в пространстве», «Перпендикулярность в пространстве», «Многогранники», «Координаты и векторы в пространстве», «Тела вращения», «Объёмы тел. Площадь сферы», «Геометрия в историческом развитии».

В разделе «Параллельность в пространстве» вводится понятие параллельности прямой и плоскости, которое служит фундаментом гибкого и мощного аппарата, используемого в решении геометрических задач.

В задачи изучения раздела «Перпендикулярность в пространстве» входит развитие умения решать задачи рациональными методами, вносить необходимые коррективы в ходе решения задачи.

Особенностью раздела «Многогранники» является то, что материал данного раздела носит прикладной характер и учитывает взаимосвязь системы научных знаний и метода познания — математического моделирования, обладает широкими возможностями для развития алгоритмического мышления, обеспечивает опыт продуктивной деятельности, обеспечивающий развитие мотивации к обучению и интеллекта.

Раздел «Координаты и векторы в пространстве» расширяет понятия, изученные в курсе геометрии 7—9 классов, а также методы исследования. Целью изучения данного раздела является формирование умения применять координатный метод для решения различных геометрических задач.

Материал раздела «Тела вращения» способствует развитию самостоятельности в организации и проведении исследований, воображения и творческих способностей учащихся.

Материал раздела «Объёмы тел. Площадь сферы» формирует представления об общих идеях и методах математического анализа и геометрии. Цель изучения раздела — применение математического аппарата для решения математических и практических задач, а также для доказательства ряда теорем.

Раздел «Геометрия в историческом развитии» позволяет сформировать представление о культурных и исторических факторах становления математики как науки, о ценности математических знаний и их применений в современном мире, о связи научного знания и ценностных установок

Место учебного предмета в Базисном учебном (образовательном) плане

   В базисном учебном (образовательном) плане на изучение алгебры и начал математического анализа и геометрии в 10— 11 классах основной школы отведено 4 учебных часа в неделю в течение каждого года обучения.

Данная рабочая программа по математике разработана для классов гуманитарной направленности, рассчитана на 4 часа в неделю, всего 140 часов в год и для классов математической направленности, рассчитана на 4+2 часа в год. Поскольку при таком количестве часов невозможно деление предмета «Математика» на «Алгебру и начала математического анализа» и «Геометрию», авторские рабочие программы к данному УМК были переработаны, поскольку рассчитаны на преподавание математики при пяти часах в неделю: три часа – на алгебру и начала анализа, два часа - на геометрию. В рамках единого курса целесообразно изучать материал блоками.

Личностные, метапредметные и предметные результаты освоенияучебного курса математики в основной общеобразовательной школе.

4.1. Личностные и метапредметные результаты

4.1.1. Личностные результаты, формированию которых способствует изучение данного учебного предмета, раскрывающие и конкретизирующие содержаниеПриложения № 1 к основной образовательной программе основного общегообразования.

4.1.2. Метапредметные результаты, формированию которых способствует изучение данного учебного предмета, раскрывающие и конкретизирующие содержание Приложения №2 к основной образовательной программе основного

4.2. Предметные результаты

4.2.1. Предметные результаты освоения учебного курса математика, раскрывающие и конкретизирующие содержание Приложения № 3 к основной образовательной программе основного общего образования

Приложение №1

№ моду-ля	Образовательный результат	Кол-во лет на освоение	Клас-сы
Личностные результаты:
1.	воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;	7	5-11
2.	ответственное отношение к обучению, готовность и способность к саморазвитию и самообразованию на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;	2	10-11
3.	осознанный выбор будущей профессиональной деятельности на базе ориентировки в мире профессий и профессиональных предпочтений; отношение к профессиональной деятельности как к возможности участия в решении личных, общественных, государственных и общенациональных проблем; формирование уважительного отношения к труду, развитие опыта участия в социально значимом труде	2	10-11
4.	умение контролировать процесс и результат учебной и математической деятельности;	7	5-11
5.	критичность мышления, инициатива, находчивость, активность при решении математических задач;	7	5-11
6.	формирование мировоззрения, соответствующего современному уровню развития науки и общественной практики;	2	10-11
7.	умение управлять своей познавательной деятельностью;	2	10-11
8.	умение взаимодействовать с одноклассниками, детьми младшего возраста и взрослыми в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности.	2	10-11

Приложение № 2

№ модуля	Образовательный результат	Кол-во летнаосвоение	Классы	Подлежит липромежуточнойаттестации
Метапредметные результаты: 1. Регулятивные
1.	умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учёбе, развивать мотивы и интересы своей познавательной деятельности;	7	5-11	нет
2	умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;	7	5-11	нет
3.	умение самостоятельно принимать решения, проводить анализ своей деятельности, применять различные методы познания	2	10-11	нет
4.	владение навыками познавательной, учебно-исследовательской и проектной деятельности	2	10-11
2. Познавательные
1	формирование понятийного аппарата, умения создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;	5	5-11	нет
2	умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы;	5	5-11	нет
3	формирование компетентности в области использования информационно-коммуникационных технологий;	2	10-11	Нет
4	умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;	5	5-9	Нет
5	умение самостоятельно осуществлять поиск в различных источниках, отбор, анализ, систематизацию и классификацию информации, необходимой для решения математических проблем, представлять её в понятной форме; принимать решение в условиях неполной или избыточной, точной или вероятностной информации; критически оценивать и интерпретировать информацию, получаемую из различных источников	2	10-11	Нет
6	умение понимать и использовать математические средства наглядности (графики, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;	7	5-11	Нет
7	умение выдвигать гипотезы при решении задачи, понимать необходимость их проверки;	7	5-11	Нет
8	понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом	7	5-11	Нет
3. Коммуникативные
1	формирование умений работать в группе с выполнением различных социальных ролей,	7	5-11	нет
2	представлять и отстаивать свои взгляды и убеждения, вести дискуссию	7	5-11	нет
3	развитие монологической и диалогической речи, умения выражать свои мысли и выслушивать собеседника,	7	5-11	нет
4	воспитание сдержанности, культуры взаимоотношений;	7	5-11	нет

Приложение № 3

№ модуля	Предметный результат	Кол-во летнаосвоение	Классы	Подлежит липромежуточнойаттестации
1.	осознание значения математики для повседневной жизни человека;	2	10-11	нет
2	представление о математической науке как сфере математической деятельности, об этапах её развития, о её значимости для развития цивилизации;	2	10-11	нет
3	умение описывать явления реального мира на математическом языке; представление о математических понятиях и математических моделях как о важнейшем инструментарии, позволяющем описывать и изучать разные процессы и явления;	2	10-11	нет
4	представление об основных понятиях, идеях и методах алгебры и математического анализа;	2	10-11	да
5	представление о процессах и явлениях, имеющих вероятностный характер, о статистических закономерностях в реальном мире, об основных понятиях элементарной теории вероятностей; умение находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;	2	10-11	да
6	владение методами доказательств и алгоритмами решения; умение их применять, проводить доказательные рассуждения в ходе решения задач;	2	10-11	да
7	выполнять вычисления с действительными и комплексными числами;	2	10-11	Да
8	решать рациональные, иррациональные, показа- тельные, степенные и тригонометрические уравнения, неравенства, системы уравнений и неравенств;	2	10-11	да
9	решать текстовые задачи арифметическим способом, с помощью составления и решения уравнений, систем уравнений и неравенств;	2	10-11	да
10	использовать алгебраический язык для описания предметов окружающего мира и создания соответствующих математических моделей;	2	10-11	да
11	выполнять тождественные преобразования рациональных, иррациональных, показательных, степенных, тригонометрических выражений;	2	10-11	да
12	выполнять операции над множествами;	2	10-11	да
13	исследовать функции с помощью производной и строить их графики;	2	10-11	да
14	вычислять площади фигур и объёмы тел с помощью определённого интеграла;	2	10-11	да
15	проводить вычисления статистических характеристик, выполнять приближённые вычисления;	2	10-11	да
16	решать комбинаторные задачи;	2	10-11	да
17	владение навыками использования компьютерных программ при решении математических задач.	2	10-11	да
18	представление об основных понятиях, идеях и методах геометрии;	2	10-11	Да
19	практически значимые математические умения и навыки, способность их применения к решению математических и нематематических задач;	2	10-11	да

Планируемые результаты обучения алгебре и началам анализа

Числа и вычисления

По окончании изучения курса учащийся научится:

• оперировать понятием «радианная мера угла», выполнять преобразования радианной меры в градусную и градусной меры в радианную;

• оперировать понятием «комплексное число», выполнять арифметические операции с комплексными числами;

• изображать комплексные числа на комплексной плоскости, находить комплексную координату числа.

Учащийся получит возможность:

• использовать различные меры измерения углов при решении геометрических задач, а также задач из смежных дисциплин;

• применять комплексные числа для решения алгебраических уравнений.

Выражения

По окончании изучения курса учащийся научится:

• оперировать понятиями корня n-й степени, степени с рациональным показателем, степени с действительным показателем, логарифма;

• применять понятия корня n-й степени, степени с рациональным показателем, степени с действительным показателем, логарифма и их свойства в вычислениях и при решении задач;

• выполнять тождественные преобразования выражений, содержащих корень n-й степени, степени с рациональным показателем, степени с действительным показателем, логарифм;

• оперировать понятиями: косинус, синус, тангенс, котангенс угла поворота, арккосинус, арксинус, арктангенс и арккотангенс;

• выполнять тождественные преобразования тригонометрических выражений.

Учащийся получит возможность:

• выполнять многошаговые преобразования выражений, применяя широкий набор способов и приёмов;

• применять тождественные преобразования выражений для решения задач из различных разделов курса..

Уравнения и неравенства

По окончании изучения курса учащийся научится:

• решать иррациональные, тригонометрические, показательные и логарифмические уравнения, неравенства и их системы;

• решать алгебраические уравнения на множестве комплексных чисел;

• понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;

• применять графические представления для исследования уравнений.
  
  

Учащийся получит возможность:

• овладеть приёмами решения уравнений, неравенств и систем уравнений; применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;

• применять графические представления для исследования уравнений, неравенств, систем уравнений, содержащих параметры.

Функции

По окончании изучения курса учащийся научится:

• понимать и использовать функциональные понятия, язык (термины, символические обозначения);

• выполнять построение графиков функций с помощью геометрических преобразований;

• выполнять построение графиков вида 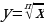, степенных, тригонометрических, обратных тригонометрических, показательных и логарифмических функций;

• исследовать свойства функций;

• понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами..

Учащийся получит возможность:

• проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера;

• использовать функциональные представления и свойства функций для решения задач из различных разделов курса математики

Элементы математического анализа

Выпускник научится

• понимать терминологию и символику, связанную с понятиями производной, первообразной и интеграла;

• решать неравенства методом интервалов;

• вычислять производную и первообразную функции;

• использовать производную для исследования и построения графиков функций;

• понимать геометрический смысл производной и определённого интеграла;

• вычислять определённый интеграл.

Выпускник получит возможность:

• сформировать представление о пределе функции в точке;

• сформировать представление о применении геометрического смысла производной и интеграла в курсе математики, в смежных дисциплинах;

• сформировать и углубить знания об интеграле.
  
  

Вероятность и статистика. Работа с данными.

Выпускник научится:

• решать комбинаторные задачи на нахождение количества объектов или комбинаций;

• применять формулу бинома Ньютона для преобразования выражений;

• использовать метод математической индукции для доказательства теорем и решения задач;

• использовать способы представления и анализа статистических данных;

• выполнять операции над событиями и вероятностями.
  
  

Выпускник получит возможность:

• научиться специальным приёмам решения комбинаторных задач;

• характеризовать процессы и явления, имеющие вероятностный характер.
  
  

Планируемые результаты обучения геометрии

Выпускник научится:

• оперировать понятиями: точка, прямая, плоскость в пространстве, параллельность и перпендикулярность прямых и плоскостей;

• распознавать основные виды многогранников (призма, пирамида, прямоугольный параллелепипед, куб);

• изображать геометрические фигуры с помощью чертёжных инструментов;

• извлекать информацию о пространственных геометрических фигурах, представленную на чертежах;

• применять теорему Пифагора при вычислении элементов стереометрических фигур;

• находить объёмы и площади поверхностей простейших многогранников с применением формул;

• распознавать тела вращения: конус, цилиндр, сферу и шар;

• вычислять объёмы и площади поверхностей простейших многогранников и тел вращения с помощью формул;

• оперировать понятием «декартовы координаты в пространстве»;

• находить координаты вершин куба и прямоугольного параллелепипеда;

• находить примеры математических открытий и их авторов, в связи с отечественной и всемирной историей;

• понимать роль математики в развитии России.

В повседневной жизни и при изучении других предметов:

• соотносить абстрактные геометрические понятия и факты с реальными жизненными объектами и ситуациями;

• использовать свойства пространственных геометрических фигур для решения задач практического содержания;

• соотносить площади поверхностей тел одинаковой формы и различного размера;

• оценивать форму правильного многогранника после спилов, срезов и т. п. (определять количество вершин, рёбер и граней полученных многогранников).

Выпускник получит возможность:

• применять для решения задач геометрические факты, если условия применения заданы в явной форме;

• решать задачи на нахождение геометрических величин по образцам или алгоритмам;

• делать плоские (выносные) чертежи из рисунков объемных фигур, в том числе рисовать вид сверху, сбоку, строить сечения многогранников;

• извлекать, интерпретировать и преобразовывать информацию о геометрических фигурах, представленную на чертежах;

• применять геометрические факты для решения задач, в том числе предполагающих несколько шагов решения;

• описывать взаимное расположение прямых и плоскостей в пространстве;

• формулировать свойства и признаки фигур;

• доказывать геометрические утверждения;

• задавать плоскость уравнением в декартовой системе координат;

• владеть стандартной классификацией пространственных фигур (пирамиды, призмы, параллелепипеды);

• использовать свойства геометрических фигур для решения задач практического характера и задач из других областей знаний;

• решать простейшие задачи введением векторного базиса.

Содержание курса

Алгебра и начала анализа

• Числа и величины

Радианная мера угла. Связь радианной меры угла с градусной мерой.

Расширение понятия числа: натуральные, целые, рациональные, действительные, комплексные числа. Комплексные числа и их геометрическая интерпретация. Сопряжённые комплексные числа. Действительная и мнимая части, модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы записи комплексных чисел. Арифметические операции с комплексными числами. Натуральная степень комплексного

числа. Формула Муавра.

• Выражения

Корень n-й степени. Арифметический корень n-й степени. Свойства корня n-й степени. Тождественные преобразования выражений, содержащих корни n-й степени. Вынесение множителя из-под знака корня. Внесение множителя под знак корня.

Степень с рациональным показателем. Свойства степени с рациональным показателем. Тождественные преобразования выражений, содержащих степени с рациональным показателем.

Косинус, синус, тангенс, котангенс угла поворота. Основные соотношения между косинусом, синусом, тангенсом и котангенсом одного и того же аргумента. Формулы сложения. Формулы приведения. Формулы двойного и половинного углов. Формулы суммы и разности синусов (косинусов). Формулы преобразования произведения в сумму. Тождественные преобразования выражений, содержащих косинусы, синусы, тангенсы и котангенсы. Арккосинус, арксинус, арктангенс, арккотангенс. Простейшие свойства арккосинуса, арксинуса, арктангенса, арккотангенса.

Степень с действительным показателем. Свойства степени с действительным показателем. Тождественные преобразования выражений, содержащих степени с действительным показателем.

Логарифм. Свойства логарифмов. Тождественные преобразования выражений, содержащих логарифмы.

• Уравнения и неравенства.

Область определения уравнения (неравенства). Равносильные уравнения (неравенства). Равносильные преобразования уравнений (неравенств). Уравнение-следствие (неравенство-следствие). Посторонние корни.

Иррациональные уравнения (неравенства). Метод равносильных преобразований для решения иррациональных уравнений (неравенств). Метод следствий для решения иррациональных уравнений. Тригонометрические уравнения (неравенства). Основные тригонометрические уравнения (неравенства) и методы их решения.

Тригонометрические уравнения, сводящиеся к алгебраическим. Однородные уравнения первой и второй степеней. Решение тригонометрических уравнений методом разложения на множители.

Показательные уравнения (неравенства). Равносильные преобразования показательных уравнений (неравенств). Показательные уравнения (неравенства), сводящиеся к алгебраическим.

Логарифмические уравнения (неравенства). Равносильные преобразования логарифмических уравнений (неравенств). Логарифмические уравнения (неравенства), сводящиеся к алгебраическим.

Решение алгебраических уравнений на множестве комплексных чисел. Основная теорема алгебры.

• Функции

Наибольшее и наименьшее значения функции. Чётные и нечётные функции. Свойства графиков чётной и нечётной функций.

Построение графиков функций с помощью геометрических преобразований (параллельных переносов, сжатий, растяжений, симметрий).

Обратимые функции. Связь возрастания и убывания функции с её обратимостью. Взаимно обратные функции. Свойства графиков взаимно обратных функций.

Степенная функция. Степенная функция с натуральным (целым) показателем. Свойства степенной функции с натуральным (целым) показателем. График степенной функции с натуральным (целым) показателем.

Функция 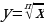.. Взаимообратность функций 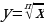и степенной функции с натуральным показателем. Свойства функции 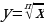и её график.

Периодические функции. Период периодической функции. Главный период. Свойства графика периодической функции.

Тригонометрические функции: косинус, синус, тангенс, котангенс. Знаки значений тригонометрических функций. Чётность и нечётность тригонометрических функций. Периодичность тригонометрических функций.

Свойства тригонометрических функций. Графики тригонометрических функций.

Обратные тригонометрические функции. Свойства обратных тригонометрических функций и их графики.

Показательная функция. Свойства показательной функции и её график.

Логарифмическая функция. Свойства логарифмической функции и её график.

• Элементы математического анализа

Предел функции в точке. Непрерывность. Промежутки знакопостоянства непрерывной функции. Непрерывность рациональной функции. Метод интервалов.

Задачи, приводящие к понятию производной. Производная функции в точке. Таблица производных. Правила вычисления производных. Механический и геометрический смысл производной. Уравнение касательной к графику функции. Признаки возрастания и убывания функции. Точки экстремума функции. Метод нахождения наибольшего и наименьшего значений функции. Построение графиков функций.

Первообразная функция. Общий вид первообразных. Неопределённый интеграл. Таблица первообразных функций. Правила нахождения первообразной функции. Определённый интеграл. Формула Ньютона — Лейбница. Методы нахождения площади фигур и объёма тел, ограниченных данными линиями и поверхностями.

• Вероятность и статистика. Работа с данными.

Повторение. Решение задач на табличное и графическое представление данных. Использование свойств и характеристик числовых наборов: средних, наибольшего и наименьшего значений, размаха, дисперсии. Решение задач на определение частоты и вероятности событий. Вычисление вероятностей в опытах с равновозможными элементарными исходами. Решение задач с применением комбинаторики. Решение задач на вычисление вероятностей независимых событий, применение формулы сложения вероятностей. Решение задач с применением диаграмм Эйлера, дерева вероятностей, формулы Бернулли.

Условная вероятность. Правило умножения вероятностей. Формула полной вероятности.

Дискретные случайные величины и распределения. Независимые случайные величины. Распределение суммы и произведения независимых случайных величин.

Математическое ожидание и дисперсия случайной величины. Математическое ожидание и дисперсия суммы случайных величин.

Геометрическое распределение. Биномиальное распределение и его свойства.

Непрерывные случайные величины. Понятие о плотности вероятности. Равномерное распределение. Показательное распределение, его параметры. Понятие о нормальном распределении. Параметры нормального распределения. Примеры случайных величин, подчинённых нормальному закону (погрешность измерений, рост человека).

Неравенство Чебышёва. Теорема Бернулли. Закон больших чисел.

Выборочный метод измерения вероятностей. Роль закона больших чисел в науке, природе и обществе.

Ковариация двух случайных величин. Понятие о коэффициенте корреляции. Совместные наблюдения двух случайных величин. Выборочный коэффициент корреляции.

• Алгебра и начала анализа в историческом развитии

Развитие идеи числа, появление комплексных чисел и их применение. История возникновения дифференциального и интегрального исчисления. Полярная система координат. Элементарное представление о законе больших чисел.

Геометрия

• Повторение

Решение задач с применением свойств фигур на плоскости. Задачи на доказательство и построение контрпримеров. Использование в задачах простейших логических правил. Решение задач с использованием теорем о треугольниках, соотношений в прямоугольных треугольниках, фактов, связанных с четырёхугольниками. Решение задач с использованием фактов, связанных с окружностями. Решение задач на измерения на плоскости, вычисление длин и площадей. Решение задач с использованием метода координат.

• Наглядная стереометрия

Фигуры и их изображения (прямоугольный параллелепипед, куб, пирамида, призма, конус, цилиндр, сфера). Основные понятия стереометрии и их свойства. Сечения куба и тетраэдра. Точка, прямая и плоскость в пространстве, аксиомы стереометрии и следствия из них. Взаимное расположение прямых и плоскостей в пространстве. Параллельность прямых и плоскостей в пространстве. Изображение простейших пространственных фигур на плоскости.

• Параллельность и перпендикулярность в пространстве

Расстояния между фигурами в пространстве.

Углы в пространстве. Перпендикулярность прямых и плоскостей.

Проекция фигуры на плоскость. Признаки перпендикулярности прямых и плоскостей в пространстве. Теорема о трёх перпендикулярах.

• Многогранники

Параллелепипед. Свойства прямоугольного параллелепипеда. Теорема Пифагора в пространстве. Призма и пирамида. Правильная пирамида и правильная призма. Прямая пирамида. Элементы призмы и пирамиды.

Простейшие комбинации многогранников и тел вращения. Вычисление элементов пространственных фигур (рёбра, диагонали, углы).

• Тела вращения

Цилиндр, конус, сфера и шар. Основные свойства прямого кругового цилиндра, прямого кругового конуса. Изображение тел вращения на плоскости. Представление об усечённом конусе, сечениях конуса (параллельных основанию и проходящих через вершину), сечениях цилиндра (параллельно и перпендикулярно оси), сечениях шара. Развёртка цилиндра и конуса.

• Объемы тел. Площадь сферы

Понятие об объёме. Объём пирамиды и конуса, призмы и цилиндра. Объём шара.

Подобные тела в пространстве. Соотношения между площадями поверхностей и объёмами подобных тел. Площадь поверхности правильной пирамиды и прямой призмы. Площадь поверхности прямого кругового цилиндра, прямого кругового конуса и шара..

• Координаты и векторы в пространстве

Движения в пространстве: параллельный перенос, центральная симметрия, симметрия относительно плоскости, поворот. Свойства движений. Применение движений при решении задач.

Векторы и координаты в пространстве. Сумма векторов, умножение вектора на число, угол между векторами. Коллинеарные и компланарные векторы. Скалярное произведение векторов. Теорема о разложении вектора по трём некомпланарным векторам. Скалярное произведение векторов в координатах. Применение векторов при решении задач на нахождение расстояний, длин, площадей и объёмов. Уравнение плоскости в пространстве. Уравнение сферы в пространстве. Формула для вычисления расстояния между точками в пространстве.

Характеристика деятельности учащихся(на уровне учебных действий)

Алгебра и начала математического анализа 10 класс

Повторение и расширение сведений о функции

Формулировать определения наибольшего и наименьшего значений функции, чётной и нечётной функций. Формулировать теоремы о свойствах графиков чётных и нечётных функций. Находить наибольшее и наименьшее значения функции на множестве по её графику. Исследовать функцию, заданную формулой, на чётность. Строить графики функций, используя чётность или нечётность. Формулировать определение обратимой функции. Распознавать обратимую функцию по её графику. Устанавливать обратимость функции по её возрастанию или убыванию. Формулировать определение взаимно обратных функций. Проверять, являются ли две данные функции взаимно обратными. Находить обратную функцию к данной обратимой функции. По графику данной функции строить график обратной функции. Устанавливать возрастание (убывание) обратной функции по возрастанию (убыванию) данной функции.

Формулировать определения области определения уравнений (неравенств), равносильных уравнений (неравенств), уравнений-следствий (неравенств-следствий), постороннего корня. Формулировать теоремы, описывающие равносильные преобразования уравнений (неравенств).

Выполнять геометрические преобразования графиков функций, связанные с параллельными переносами, растяжениями, сжатиями и симметриями, относительно координатных осей.

Применять метод равносильных преобразований для решения уравнений и неравенств. Находить область определения уравнений и неравенств. При-

менять метод следствий для решения уравнений.

Решать неравенства методом интервалов

Степенная функция

Формулировать определение степенной функции с целым показателем. Описывать свойства степенной функции с целым показателем, выделяя

случаи чётной и нечётной степени, а также натуральной, нулевой и целой отрицательной степени. Строить графики функций на основе графика степенной функции с целым показателем. Находить наибольшее и наименьшее значения степенной

функции с целым показателем на промежутке.

Формулировать определение корня (арифметического корня) n-й степени, а также теоремы о его свойствах, выделяя случаи корней чётной и нечётной степени. Находить области определения выражений, содержащих корни n-й степени. Решать уравнения, сводящиеся к уравнению xⁿ = a. Выполнять тождественные преобразования выражений, содержащих корни n-й степени, в частности, выносить множитель из-под знака корня n-й степени, вносить множитель под знак корня n-й степени, освобождаться от иррациональности в знаменателе дроби. Описывать свойства функции 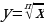, выделяя случаи корней чётной и нечётной степени. Строить графики функций на основе графика функции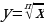

Формулировать определение степени с рациональным показателем, а также теоремы о её свойствах. Выполнять тождественные преобразования выражений, содержащих степени с рациональным показателем.

Распознавать иррациональные уравнения и неравенства. Формулировать теоремы, обосновывающие равносильность уравнений (неравенств) при возведении обеих частей данного уравнения (неравенства) в натуральную степень. Решать иррациональные уравнения методом равносильных преобразований и методом следствий. Решать иррациональные неравенства методом равносильных преобразований

Тригонометрические функции

Формулировать определение радианной меры угла. Находить радианную меру угла по его градусной мере и градусную меру угла по его радианной мере. Вычислять длины дуг окружностей.

Формулировать определения косинуса, синуса, тангенса и котангенса угла поворота. Выяснять знак значений тригонометрических функций.

Упрощать тригонометрические выражения, используя свойства чётности тригонометрических функций.

Формулировать определения периодической функции, её главного периода. Упрощать тригонометрические выражения, используя свойства периодичности тригонометрических функций.

Описывать свойства тригонометрических функций. Строить графики функций на основе графиков четырёх основных тригонометрических функций.

Преобразовывать тригонометрические выражения на основе соотношений между тригонометрическими функциями одного и того же аргумента. о значениям одной тригонометрической функции находить значения остальных тригонометрических функций того же аргумента.

Преобразовывать тригонометрические выражения на основе формул сложения. Опираясь на формулы сложения, доказывать формулы приведения, формулы двойных углов, формулы суммы и разности синусов (косинусов), формулы преобразования произведения тригонометрических функций в сумму. Преобразовывать тригонометрические выражения на основе формул приведения, формул двойных и половинных углов, формул суммы и разности синусов (косинусов), формул преобразования произведения тригонометрических функций в сумму

Тригонометрические уравнения и неравенства

Формулировать определения арккосинуса, арксинуса, арктангенса, арккотангенса. Находить значения обратных тригонометрических функций в отдельных табличных точках. Используя понятия арккосинуса, арксинуса, арктангенса, арккотангенса, решать простейшие тригонометрические уравнения.

Формулировать свойства обратных тригонометрических функций. Строить графики функций на основе графиков четырёх основных обратных тригонометрических функций. Упрощать выражения, содержащие обратные тригонометрические функции.

Распознавать тригонометрические уравнения и неравенства. Решать тригонометрические уравнения, сводящиеся к алгебраическим уравнениям, в частности, решать однородные тригонометрические уравнения первой и второй степени, а также решать тригонометрические уравнения, применяя метод разложения на множители.

Решать простейшие тригонометрические неравенства

Производная и ее применение.

Устанавливать существование предела функции в точке и находить его на основе графика функции. Различать графики непрерывных и разрывных функций.

Находить приращение аргумента и приращение функции в точке. Вычислять среднюю скорость движения материальной точки по закону её движения.

Формулировать определение производной функции в точке, правила вычисления производных. Находить производные функций, уравнения касательных графика функции, мгновенную скорость движения материальной точки. Использовать механический и геометрический смысл производной в задачах механики и геометрии.

Формулировать признаки постоянства, возрастания и убывания функции. Находить промежутки возрастания и убывания функции, заданной формулой.

Формулировать определения точки максимума и точки минимума, критической точки, теоремы, связывающие точки экстремума с производной. Находить точки экстремума функции, наибольшее и наименьшее значения функции на промежутке.

Исследовать свойства функции с помощью производной и строить график функций

Алгебра и начала математического анализа 11 класс

Показательная и логарифмическая функции

Формулировать определение показательной функции. Описывать свойства показательной функции, выделяя случай основания, большего единицы, и случай положительного основания, меньшего единицы. Преобразовывать выражения, содержащие степени с действительным показателем. Строить графики функций на основе графика показательной функции.

Распознавать показательные уравнения и неравенства. Формулировать теоремы о равносильном преобразовании показательных уравнений и неравенств. Решать показательные уравнения и неравенства.

Формулировать определение логарифма положительного числа по положительному основанию, отличному от единицы, теоремы о свойствах

логарифма. Преобразовывать выражения, содержащие логарифмы. Формулировать определение логарифмической функции и описывать её свойства, выделяя случай основания, большего единицы, и случай положительного основания, меньшего единицы. Доказывать, что показательная и логарифмическая функции являются взаимно обратными. Строить графики функций на основе логарифмической функции.

Распознавать логарифмические уравнения и неравенства. Формулировать теоремы о равносильном преобразовании логарифмических уравнений и неравенств. Решать логарифмические уравнения и неравенства.

Формулировать определения числа е, натурального логарифма. Находить производные функций, содержащих показательную функцию, логарифмическую функцию, степенную функцию с действительным показателем

Интеграл и его применение

Формулировать определение первообразной функции, теорему об основном свойстве первообразной, правила нахождения первообразной. На основе таблицы первообразных и правил нахождения первообразных находить первообразную, общий вид первообразных, неопределённый интеграл. По закону изменения скорости движения материальной точки находить закон движения материальной точки.

Формулировать теорему о связи первообразной и площади криволинейной трапеции.

Формулировать определение определённого интеграла. Используя формулу Ньютона — Лейбница, находить определённый интеграл, площади фигур, ограниченных данными линиями.

Использовать определенный интеграл для нахождения объёмов тел, в частности объёмов тел вращения.

Элементы комбинаторики. Бином Ньютона

Формулировать последовательность действий при использовании доказательства методом математической индукции. Использовать метод математической индукции для доказательства неравенств, нахождения конечных сумм, при решении задач по теории чисел.

Формулировать определение перестановки конечного множества.

Формулировать определение размещения n-элементного множества по k элементов.

Формулировать определение сочетания n-элементного множества по k элементов.

Используя формулы: количества перестановок конечного множества, размещений n-элементного множества по k элементов и сочетаний n-элементного множества по k элементов, решать задачи комбинаторного характера.

Записывать формулу бинома Ньютона.

формулировать свойства треугольника Паскаля и биноминальных коэффициентов.

Элементы теории вероятностей

Формулировать определения несовместных событий, объединения и пересечения событий, дополнения события. Используя формулу вероятности объединения двух несовместных событий, формулу, связывающую вероятности

объединения и пересечения двух событий, формулу вероятности дополнения события, находить вероятности событий.

Формулировать определения зависимых и независимых событий, условной вероятности. Используя теоремы о вероятности пересечения двух зависимых и независимых событий, теорему о вероятности пересечения нескольких независимых событий, находить вероятности событий.

Распознавать вероятностные эксперименты, описываемые с помощью схемы Бернулли. Находить вероятность события, состоящего в том, что в схеме Бернулли успехом завершится данное количество испытаний.

Формулировать определения случайной величины и множества её значений. Для случайной величины с конечным множеством значений формулировать определения распределения случайной величины и её математического ожидания. Находить математическое ожидание случайной величины по её распределению. Использовать выводы теории вероятностей в задачах с практическим жизненным содержанием

Геометрия 10 класс

Введенеи в стереометрию

Перечислять основные понятия стереометрии.

Описывать основные понятия стереометрии (точка, прямая, плоскость).

Описывать возможные способы расположения точек, прямых и плоскостей в пространстве.

Формулировать аксиомы стереометрии. Разъяснять и иллюстрировать аксиомы.

Формулировать и доказывать теоремы — следствия из аксиом.

Формулировать способы задания плоскости в пространстве.

Перечислять и описывать основные элементы многогранников: рёбра, вершины, грани.

Описывать виды многогранников (пирамида, тетраэдр, призма, прямоугольный параллелепипед, куб), а также их элементы (основания, боковые грани, рёбра основания, боковые рёбра).

Решать задачи на построение сечений многогранников.

Параллельность в пространстве

Описывать возможные способы расположения в пространстве: двух прямых, прямой и плоскости, двух плоскостей.

Формулировать определения: параллельных прямых, скрещивающихся прямых, параллельных прямой и плоскости, параллельных плоскостей, преобразование движения, фигуры, симметричной относительно точки, равных фигур, преобразования подобия.

Разъяснять понятия: преобразование фигур, параллельный перенос, параллельное проектирование, параллельная проекция ( изображение) фигуры.

Формулировать свойства параллельного проектирования.

Формулировать и доказывать признаки: параллельности двух прямых, параллельности прямой и плоскости, параллельности двух плоскостей.

Формулировать и доказывать свойства: параллельных прямых, параллельных плоскостей.

Решать задачи на построение сечений многогранников, а также построение изображений фигур

Перпендикулярность в пространстве

Формулировать определения: угла между пересекающимися прямыми; угла между скрещивающимися прямыми; прямой, перпендикулярной плоскости; угла между прямой и плоскостью; угла между двумя плоскостями; перпендикулярных плоскостей; точек, симметричных относительно плоскости; фигур, симметричных относительно плоскости; расстояния от точки до фигуры; расстояния от прямой до параллельной ей плоскости; расстояния между параллельными плоскостями; общего перпендикуляра двух скрещивающихся прямых.

Описывать понятия: перпендикуляр, наклонная, основание перпендикуляра, основание наклонной, проекция наклонной, ортогональная проекция фигуры, расстояние между скрещивающимися прямыми, зеркальная симметрия, двугранный угол, грань двугранного угла, ребро двугранного угла, линейный угол двугранного угла.

Формулировать и доказывать признаки: перпендикулярности прямой и плоскости, перпендикулярности двух плоскостей.

Формулировать и доказывать свойства: перпендикулярных прямых; прямых, перпендикулярных плоскости; перпендикулярных плоскостей.

Формулировать и доказывать теоремы: о перпендикуляре и наклонной, проведённых из одной точки; о трёх перпендикулярах; о площади ортогональной проекции выпуклого многоугольника.

Решать задачи на доказательство, а также вычисление: угла между прямыми, угла между прямой и плоскостью, угла между плоскостями, расстояния от точки до прямой, расстояния от точки до плоскости, расстояния между скрещивающимися прямыми, расстояния между параллельными плоскостями, площади ортогональной проекции выпуклого многоугольника.

Многогранники

Описывать понятия: геометрическое тело, соседние грани многогранника, плоский угол многогранника, двугранный угол многогранника, площадь поверхности многогранника, диагональное сечение призмы, противолежащие грани параллелепипеда, диагональное сечение призмы и пирамиды, усечённая пирамида.

Формулировать определения: многогранника, выпуклого многогранника, призмы, прямой призмы, правильной призмы, параллелепипеда, пирамиды, правильной пирамиды, правильного тетраэдра, высоты призмы, высоты пирамиды, высоты усечённой пирамиды, апофемы правильной пирамиды.

Формулировать и доказывать теоремы: о площади боковой поверхности прямой призмы, о диагоналях параллелепипеда, о квадрате диагонали прямоугольного параллелепипеда, о площади боковой поверхности правильной пирамиды, о площади боковой поверхности правильной усечённой пирамиды.

Решать задачи на доказательство, а также вычисление: элементов призмы и пирамиды, площади полной и боковой поверхности призмы и пирамиды.

Геометрия 11 класс

Координаты и векторы в пространстве

Описывать понятия: прямоугольная система координат в пространстве, координаты точки, вектор, сонаправленные и противоположно направленные векторы, параллельный перенос на вектор, сумма векторов, гомотетия с коэффициентом, равным k, угол между векторами.

Формулировать определения: коллинеарных векторов, равных векторов, разности векторов, противоположных векторов, произведения вектора и числа, скалярного произведения двух векторов, геометрического места точек, биссектора двугранного угла, уравнения фигуры.

Доказывать формулы: расстояния между двумя точками (с заданными координатами), координат середины отрезка, координат суммы и разности векторов, скалярного произведения двух векторов, для вычисления косинуса угла между двумя ненулевыми векторами.

Формулировать и доказывать теоремы: о координатах вектора (при заданных координатах его начала и конца), о коллинеарных векторах, о скалярном произведении двух перпендикулярных векторов, о ГМТ, равноудалённых от концов отрезка, о ГМТ, принадлежащих двугранному углу и равно удалённых от его граней, об уравнении плоскости, о векторе, перпендикулярном данной плоскости.

Применять изученные определения, теоремы и формулы к решению задач

Тела вращения

Описывать понятия: цилиндр, боковая поверхность цилиндра, поворот фигуры вокруг прямой на данный угол, тело вращения, осевое сечение цилиндра, развёртка цилиндра, боковая поверхность конуса, осевое сечение конуса, развёртка тконуса, усечённый конус, усечённая пирамида, описанная вокруг усечённого конуса, усеченная пирамида, вписанная в усечённый конус, фигура касается сферы.

Формулировать определения: призмы, вписанной в цилиндр; призмы, описанной около цилиндра; пирамиды, вписанной в конус; пирамиды, описанной около конуса; сферы и шара, а также их элементов; касательной плоскости к сфере; многогранника, вписанного в сферу; многогранника, описанного около сферы; цилиндра, вписанного в сферу; конуса, вписанного в сферу; усечённого конуса, вписанного в сферу; цилиндра, описанного около сферы, конуса, описанного около сферы; усечённого конуса, описанного около сферы.

Доказывать формулы: площади полной поверхности цилиндра, площади боковой поверхности конуса, площади боковой поверхности усечённого конуса.

Формулировать и доказывать теоремы: об уравнении сферы данного радиуса с центром в данной точке, о касательной плоскости к сфере и её следствие.

Применять изученные определения, теоремы и формулы к решению задач

Объемы тел. Площадь сферы.

Формулировать определения: объёма тела, площади поверхности шара.

Доказывать формулы: объёма призмы, объёма пирамиды, объёма усечённой пирамиды, объёма конуса, объёма усечённого конуса, объёма цилиндра, объёма шара, площади сферы.

Применять изученные определения, теоремы и формулы к решению задач

Тематическое планирование

класс	тема	Количество часов	Электронные учебно-методические материалы
10 класс	Повторение и расширение сведений о функции	8	http://fcior.edu.ru
	Степенная функция	16	http://fcior.edu.ru
	Тригонометрические функции	23	https://ege.sdamgia.ru
	Тригонометрические уравнения и неравенства	16	http://fcior.edu.ru
	Производная и ее применение	20	http://fcior.edu.ru
	Введение в стереометрию	6	http://fcior.edu.ru
	Параллельность в пространстве	9	https://ege.sdamgia.ru
	Перпендикулярность в пространстве	20	https://ege.sdamgia.ru
	Многогранники	13	http://fcior.edu.ru
11 класс	Показательная и логарифмическая функция	24	http://fcior.edu.ru
	Интеграл и его применение	12	https://ege.sdamgia.ru
	Элементы комбинаторики. Бином Ньютона	10	http://fcior.edu.ru
	Элементы теории вероятностей	12	http://fcior.edu.ru
	Координаты и векторы в пространстве	11	https://ege.sdamgia.ru
	Тела вращения	24	https://ege.sdamgia.ru
	Объемы тел. Площадь сферы	13	https://ege.sdamgia.ru

Муниципальное казенное общеобразовательное учреждение

А-Донская средняя общеобразовательная школа

Павловского муниципального района

Воронежской области

«ПРИНЯТО» «УТВЕРЖДАЮ»

на заседании педагогического совета Директор МКОУ А-Донская СОШ

Протокол № ___от ______202__ ____________ С.А.Тертышникова

Приказ от _____202__ № ______

Согласовано с Советом школы

Протокол №___ от ___202_

КАЛЕНДАРНО – ТЕМАТИЧЕСКОЕ

ПЛАНИРОВАНИЕ

Предмет - математика

Класс -11

Учебный год- 2021-2022

Учитель Антощенко Ольга Леонидовна, категория I

Александровка Донская

2021 г.

№ п/п	№ урока в разделе, теме	Тема урока	Дата по плану	Дата фактически	Домашнее задание
1	1	Степень с произвольным действительным показателем
2	2	Степень с произвольным действительным показателем
	у	Степень с произвольным действительным показателем
	у	Степень с произвольным действительным показателем
3	3	Показательные уравнения
4	4	Показательные уравнения
5	5	Показательные уравнения
6	6	Показательные неравенства
	у	Показательные уравнения
	у	Показательные неравенства
7	7	Показательные неравенства
8	8	Контрольная работа №1
9	1	Декартовы координаты точки в пространстве
10	2	Декартовы координаты точки в пространстве
	у	Декартовы координаты точки в пространстве
	у	Декартовы координаты точки в пространстве
11	3	Векторы в пространстве
12	4	Векторы в пространстве
13	5	Сложение и вычитание векторов
14	6	Сложение и вычитание векторов
	у	Сложение и вычитание векторов
	у	Сложение и вычитание векторов
15	7	Умножение вектора на число. Гомотетия
16	8	Скалярное произведение векторов
17	9	Скалярное произведение векторов
18	10	Геометрическое место точек пространства. Уравнение плоскости
	у	Скалярное произведение векторов
	у	Скалярное произведение векторов
19	11	Контрольная работа №2
20	1	Логарифм и его свойства
21	2	Логарифм и его свойства
22	3	Логарифм и его свойства
	у	Логарифм и его свойства
	у	Логарифм и его свойства
23	4	Логарифм и его свойства
24	5	Логарифмическая функция и её свойства
25	6	Логарифмическая функция и её свойства
26	7	Логарифмические уравнения
	у	Логарифмическая функция и её свойства
	у	Логарифмические уравнения
27	8	Логарифмические уравнения
28	9	Логарифмические уравнения
29	10	Логарифмические неравенства
30	11	Логарифмические неравенства
	у	Логарифмические неравенства
	у	Логарифмические неравенства
31	12	Логарифмические неравенства
32	13	Производные показательной и логарифмической функций
33	14	Производные показательной и логарифмической функций
	у	Производные показательной и логарифмической функций
	у	Производные показательной и логарифмической функций
34	15	Производные показательной и логарифмической функций
35	16	Контрольная работа №3
36	1	Цилиндр
37	2	Цилиндр
	у	Цилиндр
	у	Комбинации цилиндра и призмы
38	3	Комбинации цилиндра и призмы
39	4	Комбинации цилиндра и призмы
40	5	Конус
41	6	Конус
	у	Конус
	у	Усечённый конус
42	7	Усечённый конус
43	8	Усечённый конус
44	9	Комбинации конуса и пирамиды
45	10	Комбинации конуса и пирамиды
	у	Комбинации конуса и пирамиды
	у	Комбинации конуса и пирамиды
46	11	Комбинации конуса и пирамиды
47	12	Контрольная работа №4
48	1	Первообразная
49	2	Первообразная
	у	Первообразная
	у	Первообразная
50	3	Правила нахождения первообразной
51	4	Правила нахождения первообразной
52	5	Правила нахождения первообразной
53	6	Площадь криволинейной трапеции. Определённый интеграл
	у	Площадь криволинейной трапеции. Определённый интеграл
	у	Площадь криволинейной трапеции. Определённый интеграл
54	7	Площадь криволинейной трапеции. Определённый интеграл
55	8	Площадь криволинейной трапеции. Определённый интеграл
56	9	Площадь криволинейной трапеции. Определённый интеграл
57	10	Вычисление объёмов
	у	Вычисление объёмов
	у	Вычисление объёмов
58	11	Вычисление объёмов
59	12	Контрольная работа №5
60	1	Сфера и шар. Уравнение сферы
61	2	Сфера и шар. Уравнение сферы
	у	Сфера и шар. Уравнение сферы
	у	Сфера и шар. Уравнение сферы
62	3	Взаимное расположение сферы и плоскости
63	4	Взаимное расположение сферы и плоскости
64	5	Многогранники, вписанные в сферу
65	6	Многогранники, вписанные в сферу
	у	Многогранники, вписанные в сферу
	у	Многогранники, вписанные в сферу
66	7	Многогранники, описанные около сферы
67	8	Многогранники, описанные около сферы
68	9	Комбинации цилиндра и сферы, конуса и сферы
69	10	Комбинации цилиндра и сферы, конуса и сферы
	у	Комбинации цилиндра и сферы, конуса и сферы
	у	Комбинации цилиндра и сферы, конуса и сферы
70	11	Комбинации цилиндра и сферы, конуса и сферы
71	12	Контрольная работа №6
72	1	Метод математической индукции
73	2	Метод математической индукции
	у	Метод математической индукции
	у	Метод математической индукции
74	3	Перестановки. Размещения
75	4	Перестановки. Размещения
76	5	Перестановки. Размещения
77	6	Сочетания (комбинации)
	у	Перестановки. Размещения
	у	Сочетания (комбинации)
78	7	Сочетания (комбинации)
79	8	Бином Ньютона
80	9	Бином Ньютона
81	10	Контрольная работа №7
	у	Бином Ньютона
	у	Бином Ньютона
82	1	Объем тела. Формулы для вычисления объёма призмы
83	2	Объем тела. Формулы для вычисления объёма призмы
84	3	Формулы для вычисления объёмов пирамиды и усеченной пирамиды
85	4	Формулы для вычисления объёмов пирамиды и усеченной пирамиды
	у	Формулы для вычисления объёмов пирамиды и усеченной пирамиды
	у	Формулы для вычисления объёмов пирамиды и усеченной пирамиды
86	5	Формулы для вычисления объёмов пирамиды и усеченной пирамиды
87	6	Контрольная работа №8
88	1	Операции над событиями
89	2	Операции над событиями
	у	Операции над событиями
	у	Операции над событиями
90	3	Операции над событиями
91	4	Зависимые и независимые события
92	5	Зависимые и независимые события
93	6	Зависимые и независимые события
	у	Зависимые и независимые события
	у	Зависимые и независимые события
94	7	Схема Бернулли
95	8	Схема Бернулли
96	9	Схема Бернулли
97	10	Случайные величины и их характеристики
	у	Схема Бернулли
	у	Схема Бернулли
98	11	Случайные величины и их характеристики
99	12	Контрольная работа №9
100	1	Объемы тел вращения
101	2	Объемы тел вращения
	у	Объемы тел вращения
	у	Объемы тел вращения
102	3	Объемы тел вращения
103	4	Объемы тел вращения
104	5	Площадь сферы
105	6	Площадь сферы
	у	Площадь сферы
	у	Площадь сферы
106	7	Контрольная работа №10
107-134		Повторение
	у	Повторение (14ч)
135-136		Итоговая контрольная работа

Описание учебно-методического и материально-технического обеспечения образовательного процесса

1.Нормативные документы: Примерная программы основного общего образования по математике

2.Учебники: по алгебре для 10-11 классов, по геометрии для 10-11 классов.

• УМК А. Г. Мерзляк « Алгебра» 10-11

• УМК А. Г. Мерзляк «Геометрия 10-11»

3.Научная, научно-популярная, историческая литература.

4.Справочные пособия (энциклопедии, словари, справочники по
математике и т.п.).

5. Печатные пособия: Портреты выдающихся деятелей математики.

6. Информационные средства

• Мультимедийные обучающие программы и электронные учебные издания по основным разделам курса математики.

• Электронная база данных для создания тематических и итоговых разноуровневых тре­нировочных и проверочных материалов для органи­зации фронтальной и индивиду­альной работы.

Технические средства обучения

• Мультимедийный компьютер.

• Мультимедийный проектор.

• Интеракетивная доска

8. Учебно-практическое и учебно-лабораторное оборудование

• Доска магнитная.

• Комплект чертежных инструментов (классных и раздаточных): линейка, транспортир, угольник (30°, 60°, 90°), угольник (45°, 90°), циркуль.

• Комплекты планиметрических и стереометрических тел (демонстра­ционных и раздаточных).

• Комплект для моделирования (цветная бумага, картон, калька, клей, ножницы, пластилин).