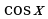Муниципальное бюджетное общеобразовательное учреждение Гиагинского района «Средняя общеобразовательная школа №8 имени В.Солдатенко»
| «Рассмотрено» Руководитель ШМО
____________ /Л.М.Сафина/ Протокол № ____________ от «___» __________ 20___г. | «Согласовано» Заместитель директора по УР
___________/Е.С.Тарасова/ | «Утверждаю» Директор МБОУ СОШ №8 им. В. Солдатенко _____________/Н.В.Усольцева/ Приказ № _________ от «_____» ___________ 20___ г. |
РАБОЧАЯ ПРОГРАММА
по математике
Уровень общего образования:
среднее общее образование: 11 класс
Учитель Сафина Лариса Михайловна
Ст.Келермесская
2022-2023 учебный год
Пояснительная записка
Рабочая программа по математике для 11 класса составлена на основе авторских программ Ю.М. Колягина, М.В. Ткачёвой, Н.Е. Фёдоровой, М.И. Шабунина «Алгебра и начала математического анализа. 10 класс» и Л.С.Атанасяна, В.Ф.Бутузова, С.Б.Кадомцева и др. «Геометрия. 10-11 класс» и ориентирована на учебники «Алгебра и начала математического анализа. 11 класс» / Ю.М. Колягин, М.В. Ткачёва, Н.Е. Фёдорова, М.И. Шабунин, — М.: Просвещение и учебник «Геометрия. 10-11 класс» / Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. — М.: Просвещение.
Планируемые предметные результаты
Тригонометрические функции
Обучающийся научится:
находить область определения и множество значений тригонометрических функций;
определять, является ли функция четной или нечётной, используя определения и свойства чётных и нечётных функций;
доказывать, что данное положительное число есть период функции;
выполнять построение графиков тригонометрических функций различного уровня сложности.
Обучающийся получит возможность научиться:
решать тригонометрические уравнения и неравенства на заданных промежутках, используя графики тригонометрических функций;
выполнять преобразования выражений, содержащих обратные тригонометрические функции;
выполнять графическое решение уравнений и неравенств, содержащих обратные тригонометрические функции.
Производная и её геометрический смысл
Обучающийся научится:
вычислять значения пределов последовательностей и функций, используя теоремы об арифметических действиях над пределами;
вычислять производные элементарных функций простого и сложного аргументов;
находить производные любой комбинации элементарных функций.
Обучающийся получит возможность научиться:
составлять уравнение касательной к графику функции;
находить угловой коэффициент прямой, заданной двумя точками;
по графику функции и касательной к графику определять значение производной в точке касания;
по графику производной функции определять количество точек, в которых касательная к графику функции параллельна прямой 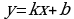 или совпадает с ней;
или совпадает с ней;
по графику функции определять в какой из указанных точек производная наименьшая.
Применение производной к исследованию функций
Обучающийся научится:
находить промежутки монотонности функции, точки экстремума и экстремумы функции, наибольшее значение непрерывной функции на отрезке, а также на интервале, содержащем единственную точку экстремума;
по графику функции определять количество целых точек, в которых производная положительна (отрицательна);
по графику функции определять в скольких из указанных точек, в которых производная положительна (отрицательна);
по графику функции определять количество точек, в которых производная равна нулю;
по графику производной функции определять количество целых точек, входящих в промежутки возрастания (убывания) функции;
по графику производной функции определять длину наибольшего (наименьшего) промежутка возрастания (убывания) функции;
по графику производной функции определять в скольких из указанные точек функция возрастает (убывает).
Обучающийся получит возможность научиться:
по графику функции определять количество точек, в которых касательная параллельна прямой вида 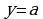 или совпадает с ней;
или совпадает с ней;
по графику функции определять сумму точек экстремума;
по графику производной функции определять количество точек максимума (минимума) функции;
по графику производной функции определять точку, в которой функция принимает наибольшее (наименьшее) значение;
определять промежутки выпуклости функции, точки перегиба;
выполнять построение графиков функции с помощью производной;
решать задачи на нахождение наибольшего (наименьшего) значения физических величин, а также геометрического содержания.
Интеграл
Обучающийся научится:
доказывать, что заданная функция 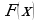 есть первообразная функции
есть первообразная функции 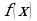 ;
;
по графику одной из первообразной определять количество точек, в которых функция равна нулю;
находить первообразные функций, используя таблицу первообразных и правила нахождения первообразных;
находить первообразную для данной функции, если график искомой первообразной проходит через заданную точку;
вычислять неопределённый интеграл по формуле Ньютона-Лейбница;
находить площадь криволинейной трапеции.
Обучающийся получит возможность научиться:
по графику функции находить разность первообразных в указанных точках;
находить площади фигур, ограниченных линиями с помощью определённого интеграла;
решать простейшие физические задачи с помощью определённого интеграла.
Комбинаторика
Обучающийся научится:
находить размещения без повторения, перестановки, сочетания, размещения с повторениями;
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля.
Обучающийся получит возможность научиться:
применять элементы комбинаторики для составления упорядоченных множеств и подмножеств данного множества.
Элементы теории вероятностей
Обучающийся научится:
вычислять вероятность события, используя классическое определение вероятности, методы комбинаторики, вероятность суммы событий;
применять формулу Бернулли.
Обучающийся получит возможность научиться:
решать задачи на вычисление вероятности совместного появления независимых событий, вероятности произведения независимых событий или событий, независимых в совокупности.
Комплексные числа
Обучающийся научится:
находить действительную и мнимую части, модуль и аргумент комплексного числа, записанного в алгебраической форме;
выполнять действия сложения, вычитания, умножения, деления комплексных чисел, записанных в алгебраической форме;
записывать комплексные числа в тригонометрической форме;
выполнять действия умножения, деления, возведения в степень и извлечения корня из комплексных чисел, записанных в тригонометрической форме.
Обучающийся получит возможность научиться:
изображать комплексные числа на комплексной плоскости;
решать простейшие задачи на нахождение на комплексной плоскости множества точек, удовлетворяющих заданному условию;
решать простейшие квадратные уравнения с комплексным неизвестным.
Уравнения и неравенства
Обучающийся научится:
изображать на координатной плоскости множества решений простейших уравнений и их систем;
находить площади фигур, ограниченных линиями, составляя систему.
Обучающийся получит возможность научиться:
находить значения параметра, при котором уравнение, система уравнений не имеет решений, имеет одно, два решения;
применять различные приемы для решения уравнений и неравенств с двумя переменными, содержащими параметры.
Геометрия
Обучающийся научится:
распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;
описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;
анализировать в простейших случаях взаимное расположение объектов в пространстве;
изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;
строить простейшие сечения куба, призмы, пирамиды;
решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);
использовать при решении стереометрических задач планиметрические факты и методы;
проводить доказательные рассуждения в ходе решения задач.
Обучающийся получит возможность научиться:
заниматься исследованием (моделированием) несложных практических ситуаций на основе изученных формул и свойств фигур;
заниматься вычислением объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Содержание учебного предмета
Повторение курса алгебры 10 класса (3 ч)
1. Тригонометрические функции (19 ч)
Область определения и множество значений тригонометрических функций. Четность, нечетность, периодичность тригонометрических функций. Свойства функции у = cosх: и ее график. Свойства функции у = sinх; и ее график. Свойства функции у = tgx и ее график. Обратные тригонометрические функции.
Основная цель — изучить свойства тригонометрических функций, научить учащихся применять эти свойства при решении уравнений и неравенств; обобщить и систематизировать знания об исследовании функций элементарными методами, научить строить графики тригонометрических функций, используя различные приемы построения графиков.
Среди тригонометрических формул следует особо выделить те формулы, которые непосредственно относятся к исследованию тригонометрических функции и построению их графиков. Так, формулы sin(-х) = -sin х и cos(-x) = cos х выражают свойства нечетности и четности функций у = sin х и у = cos х соответственно.
На профильном уровне продолжается изучение свойств элементарных функций методами элементарной математики; решаются задачи разного уровня сложности на нахождение области определения и множества значений сложных функций.
На углубленном уровне рассматриваются доказательства утверждений, являющихся отрицанием факта ограниченности функции, периодичности и пр. Логическая структура этих доказательств специально не обсуждается. Приведенные примеры рассуждений в задачах позволяют провести их анализ и направить в нужное русло поиск учащихся при самостоятельном выполнении упражнений.
Построение графиков тригонометрических функций проводится с использованием их свойств и начинается с построение графика функции у = cosх.
С помощью графиков тригонометрических функций решаются простейшие тригонометрические уравнения и неравенства.
На базовом уровне обратные тригонометрические функции даются в ознакомительном плане. Рекомендуется также рассмотреть графики функций у = |cosх|, у = а + cosх , у = cos (х + а),
у = acos х, у = cos ах, где а — некоторое число.
На профильном уровне обратные тригонометрические функции изучаются после повторения понятия\взаимно обратных функций. Применение свойств обратных тригонометрических функций рассматривается на конкретных примерах.
В ходе изучения темы особое внимание уделяется исследованию функций и построению графиков методами элементарной математики. Таким образом, при изучении данного раздела происходит как обобщение и систематизация знаний учащихся об элементарных функциях и их исследовании методами элементарной математики, так и подготовка к восприятию элементов математического анализа.
2. Производная и ее геометрический смысл (19 ч)
Предел последовательности. Предел функции. Непрерывность функции. Определение производной. Правила дифференцирования. Производная степенной функции. Производные элементарных функций. Геометрический смысл производной.
Основная цель — ввести понятие предела последовательности, предела функции, производной; научить наводить производные с помощью формул дифференцирования; научить находить уравнение касательной к графику; функции, решать практические задачи на применение понятия производной.
На базовом уровне изложение материала ведется на наглядно-интуитивном уровне: многие формулы не доказывается, а только поясняются или принимаются без доказательств. Главное — показать учащимся целесообразность, изучения производной и в дальнейшем первообразной (интеграла), так как это необходимо при решении многих практических задач, связанных с исследованием физических явлений, вычислением площадей криволинейных фигур и объемов тел с произвольными границами, с построением графиков функций. Прежде всего следует показать, что функции, графиками которых являются кривые, описывают многие важные физические и технические процессу.
На профильном уровне учащиеся знакомятся со строгими определениями предела, последовательности, предела функции, непрерывности функции. Правила дифференцирования и формулы производных элементарных функций доказываются строго.
Достаточно подробное изучение теории пределов числовых последовательностей учащимися профильных классов не просто готовит их к восприятию сложного понятия предела функции в точке, но развивает многие качества мыслительной деятельности учащихся.
3. Применение производной к исследованию функций (16 ч)
Возрастание и убывание функции. Экстремумы функции. Наибольшее и наименьшее значения функции. Производная второго порядка, выпуклость и точки перегиба. Построение графиков функций.
Основная цель — показать возможности производной в исследовании свойств функций и построении их графиков.
При изучении материала широко используются знания, полученные учащимися в ходе работы над предыдущей темой.
Обосновываются утверждения о зависимости возрастания и убывания функции от знака ее производной на данном промежутке. Вводятся понятия точек максимума и минимума, точек перегиба. Учащиеся знакомятся с новыми терминами: критические и стационарные точки.
После введения понятий максимума и минимума функции формируется представление о том, что функция может иметь экстремум в точке, в которой она не имеет производной, например, у = |х| в точке х = 0.
Определение вида экстремума предполагается связать с переменой знака производной функции при переходе через точку экстремума. Необходимо показать учащимся не только профильных классов, что это можно сделать проще — по знаку второй производной: если f"(x) 0 в некоторой стационарной точке х, то рассматриваемая стационарная точка есть точка минимума; если f"(x) f"(x) = 0, то точка х есть точка перегиба.
Приводится схема исследования основных свойств функции, предваряющая построение графика. В классах базового уровня эта схема выглядит так:
1) область определения функции;
2) точки пересечения графика с осями координат;
3) производная функции и стационарные точки;
4) промежутки монотонности;
5) точки экстремума и значения функции в этих точках.
На профильном уровне (после изучения второй производной) схема исследования функции выглядит так:
1) область определения функции; четность (нечетность); периодичность;
2) нули функции; промежутки знако-постоянства;
3) асимптоты графика функции;
4) первёя производная; критические точки; промежутки монотонности; экстремумы;
5) вторая производная; промежутки выпуклости, направления выпуклостей и точки перегиба.
4. Первообразная и интеграл (15 ч)
Первообразная. Правила нахождения первообразных. Площадь криволинейной трапеции. Интеграл и его вычисление. Вычисление площадей фигур с помощью интегралов. Применение интегралов для решения физических задач. Простейшие дифференциальные уравнения.
Основная цель — ознакомить с понятием интеграла и интегрированием как операцией, обратной дифференцированию; научить находить площадь криволинейной трапеции, решать простейшие физические задачи с помощью интеграла.
Операция интегрирования сначала определяется как операция, обратная дифференцированию, далее вводится понятие первообразной, при этом не вводится ни определение неопределенного интеграла, ни его обозначение. Таблица правил интегрирования (т. е. таблица первообразных) в этом случае естественно получается из таблицы производных. Формулируется утверждение, что все первообразные для функции f(x) имеют вид F(x) + С, где F(x) — первообразная, найденная в таблице. Этот факт не доказывается, а только поясняется.
Связь между первообразной и площадью криволинейной трапеции устанавливается формулой Ньютона — Лейбница. Далее возникает определенный интеграл как предел интегральной суммы; при этом формула Ньютона — Лейбница также оказывается справедливой. Таким образом, эта формула является главной: с ее помощью вычисляются определенные интегралы и находятся площади криволинейных трапеций.
На профильном уровне учащиеся знакомятся с задачами на нахождение пути по заданной скорости, на вычисление работы переменной силы, задачами о размножении бактерий и о радиоактивном распаде более подробно, чем школьники классов базового уровня, и учатся решать простейшие дифференциальные уравнения.
5. Комбинаторика (9 ч)
Математическая индукция. Правило произведения. Размещения с повторениями. Перестановки. Размещения без повторений. Сочетания без повторений и бином Ньютона.
Основная цель — развить комбинаторное мышление учащихся; ознакомить с теорией соединений (как самостоятельным разделом математики и в дальнейшем — с аппаратом решения ряда вероятностных задач); обосновать формулу бинома Ньютона (с которой учащиеся лишь ' знакомились в курсе 10 класса).
Основными задачами комбинаторики считаются следующие: 1) составление упорядоченных множеств (образование перестановок); 2) составление подмножеств данного множества (образование сочетаний); 3) составление упорядоченных подмножеств данного множества (образование размещений).
Из всего многообразия вопросов, которыми занимается комбинаторика, в содержание образования старшей школы сегодня включается лишь теория соединений — комбинаторных конфигураций, которые называются перестановками, размещениями и сочетаниями. Причем обязательными для изучения являются лишь соединения без повторений — соединения, составляемые по определенным правилам из различных элементов.
Теория соединений с повторениями не является обязательной для изучения даже на профильном уровне, тем не менее, полезно ввести понятие хотя бы размещений с повторениями, так как задачи на подсчет числа этих размещений рассматриваются уже на первых уроках при решении задач на применение правила произведения.
Знакомство с остальными соединениями с повторениями может быть рассмотрено с учащимися профильных классов при наличии времени. Доказательство же справедливости формул для подсчета числа перестановок с повторениями и числа сочетаний с повторениями следует рассматривать только при углубленном изучении с учащимися, усвоившими применение метода математической индукции.
Дополнительной мотивацией рассмотрения, например, перестановок с повторениями является то, что биномиальные коэффициенты есть не что иное, как перестановки с повторениями. Поэтому учащиеся, знакомые с понятием перестановок с повторениями, легко воспринимают вывод формулы бинома Ньютона.
Элементы теории вероятностей (8 ч)
Вероятность события. Сложение вероятностей. Условная вероятность. Независимость событий. Вероятность произведения независимых событий. Формула Бернулли.
Основная цель — сформировать понятие вероятности случайного независимого события; научить решать задачи на применение теоремы о вероятности суммы двух несовместных событий и на нахождение вероятности произведения двух независимых событий.
В программу включено изучение (частично на интуитивном уровне) лишь отдельных элементов теории вероятностей. При этом введению каждого понятия предшествует неформальное объяснение, раскрывающее сущность данного понятия, его происхождение и реальный смысл. Так вводятся понятия случайных, достоверных и невозможных событий, связанных с некоторым испытанием; определяются и иллюстрируются операции над событиями.
Классическое определение вероятности события с рав- новозможными элементарными исходами формулируется строго, и на его основе (с использованием знаний комбинаторики) решается большинство задач/Понятия геометрической вероятности и статистической вероятности вводились на интуитивном уровне в основной школе.
Независимость событий вводится достаточно строго (после определения понятия условной вероятности). Разбирается решение задачи на нахождение вероятности события В, состоящего в том, что при испытаниях наблюдаемое событие А произойдет ровно k раз, после чего обосновывается формула Бернулли.
При изложении материала данного раздела подчеркивается прикладное значение теории вероятностей в различных областях знаний и практической деятельности человека.
Комплексные числа (13 ч)
Определение комплексных чисел. Сложение и умножение комплексных чисел. Комплексно сопряженные числа. Модуль комплексного числа. Операции вычитания и деления. Геометрическая интерпретация комплексного числа. Тригонометрическая форма комплексного числа. Умножение и деление комплексных чисел, записанных в тригонометрической форме. Формула Муавра. Квадратное уравнение с комплексным неизвестным. Извлечение корня из , комплексного числа. Алгебраические уравнения.
Основная цель — научить представлять комплексное число в алгебраической и тригонометрической формах; изображать число на комплексной плоскости; научить выполнять операции сложения,t вычитания, умножения и де- 1 ления чисел, записанных в алгебраической форме, операции умножения и деления чисел, представленных в тригонометрической форме.
На примере теории комплексных чисел старшеклассни- 1 ки впервые (а, возможно, и вообще единственный раз) знакомятся со строгим построением теории чисел.
Комплексные числа вводятся либо как упорядоченная пара чисел, либо как выражение а + bi, где а и b — действительные числа, i — некоторый символ, такой, что i2 = -1. Затем формулируются правила, устанавливающие равенство комплексных чисел, вводятся числа, соответствующие привычным для школьников нулю и единице, изучаются правила арифметических действий над комплексными числами.
Тригонометрическая интерпретация комплексного числа позволяет решать алгебраические уравнения (в частности, квадратные) в поле комплексных чисел и осознанно воспринимать основную теорему алгебры, которая формулируется в конце темы.
8. Повторение курса алгебры и начал математического анализа (Уравнения и неравенства. Задачи с параметром) (21 ч)
Методы решения уравнений с одним неизвестным. Приёмы решения уравнений с двумя неизвестными. Неравенства, системы и совокупности неравенств с одним неизвестным. Методы их решения. Способы и методы решения систем уравнений с двумя неизвестными. Изображение на координатной плоскости решений неравенств и систем неравенств с двумя неизвестными. Подходы к решению задач с параметром.
Основная цель — обучить приемам решения уравнений, неравенств и систем уравнений и неравенств с двумя переменными.
Изображение множества точек, являющегося решением уравнения первой степени с двумя неизвестными, не ново для учащихся старших классов. Решение систем уравнений с помощью графика знакомо школьникам с основной колы. Теперь им предстоит углубить знания, полученные ранее, и ознакомиться с решением неравенств с двумя переменными и их систем.
Учебный материал этой темы построен так, что учащиеся постигают его в ходе решения конкретных задач, а затем происходит обобщение изученных примеров. Сначала рассматриваются уравнения с двумя переменными, линейные или нелинейные, затем неравенства и, наконец, системы уравнений и неравенств. Изучением этой темы подводится итог известным учащимся методам решения уравнений и неравенств. Рассмариваются методы, с которыми они ранее знакомы не были, но знания, кот
Геометрия
Координаты и векторы (15ч)
Декартовы координаты в пространстве. Формула расстояния между двумя точками. Уравнения сферы и плоскости. Формула расстояния от точки до плоскости.
Векторы. Угол между векторами. Координаты вектора. Скалярное произведение векторов. Длина вектора в координатах, угол между векторами в координатах. Коллинеарные векторы, коллинеарность векторов в координатах.
Тела и поверхности вращения (14ч)
Цилиндр и конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения параллельные основанию.
Шар и сфера, их сечения, касательная плоскость к сфере.
Объемы тел и площади их поверхностей (22ч)
Понятие об объеме тела. Отношение объемов подобных тел.
Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формулы объема шара и площади сферы.
Повторение курса стереометрии 10-11 классов (17 ч)
Итоговое повторение курса математики (13ч)
Календарно-тематическое планирование по математике для 11 класса
на 2022-2023 учебный год
| № п/п | №
| Тема урока | Дата |
| план | факт |
| 1.Повторение курса алгебры и начал математического анализа 10 класса (3ч) |
| 1 | 1.1 | Тригонометрические формулы, уравнения. |
|
|
| 2 | 1.2 | Логарифмические, показательные уравнения и неравенства. |
|
|
| 3 | 1.3 | Входной контроль знаний. |
|
|
| 2. Тригонометрические функции (19ч) |
| 4 | 2.1 | Работа над ошибками. Область определения и множество значений тригонометрических функций. |
|
|
| 5 | 2.2 | Множество значений тригонометрических функций. |
|
|
| 6 | 2.3 | Чётность, нечётность тригонометрических функций. |
|
|
| 7 | 2.4 | Периодичность тригонометрических функций. |
|
|
| 8 | 2.5 | Самостоятельная работа по теме «Чётность, нечётность, периодичность тригонометрических функций». |
|
|
| 9 | 2.6 | Функция 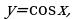 ее свойства и график. ее свойства и график. |
|
|
| 10 | 2.7 | Функция 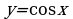 . Графическое решение тригонометрических уравнений и неравенств. . Графическое решение тригонометрических уравнений и неравенств. |
|
|
| 11 | 2.8 | Функция 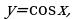 ее свойства и график. ее свойства и график. |
|
|
| 12 | 2.9 | Функция 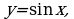 ее свойства и график. ее свойства и график. |
|
|
| 13 | 2.10 | Функция 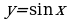 . Графическое решение тригонометрических уравнений и неравенств. . Графическое решение тригонометрических уравнений и неравенств. |
|
|
| 14 | 2.11 | Функция 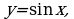 ее свойства и график. ее свойства и график. |
|
|
| 15 | 212 | Функции 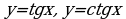 их свойства и графики. их свойства и графики. |
|
|
| 16 | 2.13 | Функции 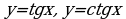 . Графическое решение тригонометрических уравнений и неравенств. . Графическое решение тригонометрических уравнений и неравенств. |
|
|
| 17 | 2.14 | Обратные тригонометрические функции. |
|
|
| 18 | 2.15 | Решение уравнений и неравенств, содержащих обратные тригонометрические функции. |
|
|
| 19 | 2.16 | Обратные тригонометрические функции. |
|
|
| 20 | 2.17 | Урок обобщения и систематизации знаний по теме «Тригонометрические функции». |
|
|
| 21 | 2.18 | Урок обобщения и систематизации знаний по теме «Тригонометрические функции». |
|
|
| 22 | 2.19 | Контрольная работа №1 по теме «Тригонометрические функции». |
|
|
| 3. Метод координат в пространстве (15ч) |
| 23 | 3.1 | Работа над ошибками. Прямоугольная система координат в пространстве. |
|
|
| 24 | 3.2 | Координаты вектора. |
|
|
| 25 | 3.3 | Решение задач на применение координат вектора. |
|
|
| 26 | 3.4 | Связь между координатами векторов и координатами точек. |
|
|
| 27 | 3.5 | Простейшие задачи в координатах. |
|
|
| 28 | 3.6 | Зачёт №1 по теме «Простейшие задачи в координатах». |
|
|
| 29 | 3.7 | Контрольная работа №2 по теме «Метод координат». |
|
|
| 30 | 3.8 | Работа над ошибками. Угол между векторами. Скалярное произведение векторов. |
|
|
| 31 | 3.9 | Решение задач по теме «Применение скалярного произведения векторов». |
|
|
| 32 | 3.10 | Вычисление углов между прямыми и плоскостями. |
|
|
| 33 | 3.11 | Повторение вопросов теории и решение задач. Самостоятельная работа. |
|
|
| 34 | 3.12 | Центральная симметрия. Осевая симметрия. Зеркальная симметрия. |
|
|
| 35 | 3.13 | Параллельный перенос. |
|
|
| 36 | 3.14 | Контрольная работа №3 по теме «Скалярное произведение векторов». |
|
|
| 37 | 3.15 | Зачёт №2 по теме «Метод координат в пространстве». |
|
|
| 4. Производная и её геометрический смысл (19ч) |
| 38 | 4.1 | Работа над ошибками. Предел последовательности (определение и свойства). |
|
|
| 39 | 4.2 | Вычисление пределов последовательностей. |
|
|
| 40 | 4.3 | Предел функции (определение, свойства). Вычисление пределов функций. |
|
|
| 41 | 4.4 | Непрерывность функции. |
|
|
| 42 | 4.5 | Определение производной. |
|
|
| 43 | 4.6 | Вычисление производной функции по определению. |
|
|
| 44 | 4.7 | Дифференцирование суммы, произведения и частного. |
|
|
| 45 | 4.8 | Дифференцирование сложной и обратной функции. |
|
|
| 46 | 4.9 | Правила дифференцирования. |
|
|
| 47 | 4.10 | Производная степенной функции. |
|
|
| 48 | 4.11 | Производная степенной функции. |
|
|
| 49 | 4.12 | Производные некоторых элементарных функций. |
|
|
| 50 | 4.13 | Решение задач на нахождение производных элементарных функций. |
|
|
| 51 | 4.14 | Производные некоторых элементарных функций. |
|
|
| 52 | 4.15 | Геометрический смысл производной. |
|
|
| 53 | 4.16 | Уравнение касательной к графику функции. |
|
|
| 54 | 4.17 | Геометрический смысл производной. |
|
|
| 55 | 4.18 | Урок обобщения и систематизации знаний по теме «Производная и ее геометрический смысл». |
|
|
| 56 | 4.19 | Контрольная работа №4 по теме «Производная и ее геометрический смысл». |
|
|
| 5. Применение производной к исследованию функций (16ч) |
| 57 | 5.1 | Работа над ошибками. Возрастание и убывание функции. |
|
|
| 58 | 5.2 | Возрастание и убывание функции. Решение задач. |
|
|
| 59 | 5.3 | Экстремумы функции. |
|
|
| 60 | 5.4 | Экстремумы функции. Решение задач. |
|
|
| 61 | 5.5 | Возрастание и убывание, экстремумы функции. |
|
|
| 62 | 5.6 | Наибольшее и наименьшее значения функции, непрерывной на отрезке (изучение алгоритма). |
|
|
| 63 | 5.7 | Задачи на нахождение наибольшего (наименьшего) значения величин. |
|
|
| 64 | 5.8 | Наибольшее и наименьшее значения функции. |
|
|
| 65 | 5.9 | Производная второго порядка, выпуклость и точки перегиба. |
|
|
| 66 | 5.10 | Асимптоты графиков функций. |
|
|
| 67 | 5.11 | Применение производной к построению графиков функций (изучение алгоритма). |
|
|
| 68 | 5.12 | Построение графиков функции с помощью производной, содержащих асимптоты. |
|
|
| 69 | 5.13 | Применение производной к построению графиков функций, содержащих асимптоты. |
|
|
| 70 | 5.14 | Применение производной к построению графиков функций. |
|
|
| 71 | 5.15 | Урок обобщения и систематизации знаний по теме «Применение производной к исследованию функции». |
|
|
| 72 | 5.16 | Контрольная работа №5 по теме «Применение производной к исследованию функции». |
|
|
| 6. Цилиндр, конус, шар (14ч) |
| 73 | 6.1 | Работа над ошибками. Понятие цилиндра. Площадь поверхности цилиндра. |
|
|
| 74 | 6.2 | Решение задач по теме «Площадь поверхности цилиндра». |
|
|
| 75 | 6.3 | Самостоятельная работа по теме «Площадь поверхности цилиндра». |
|
|
| 76 | 6.4 | Понятие конуса. Площадь поверхности конуса. |
|
|
| 77 | 6.5 | Усечённый конус. |
|
|
| 78 | 6.6 | Решение задач по теме «Конус». |
|
|
| 79 | 6.7 | Сфера и шар. Уравнение сферы. |
|
|
| 80 | 6.8 | Взаимное расположение сферы и плоскости. |
|
|
| 81 | 6.9 | Касательная плоскость к сфере. |
|
|
| 82 | 6.10 | Площадь сферы. |
|
|
| 83 | 6.11 | Решение задач на различные комбинации тел. |
|
|
| 84 | 6.12 | Разные задачи на многогранники, цилиндр, конус, шар. |
|
|
| 85 | 6.13 | Решение задач по теме «Тела вращения». |
|
|
| 86 | 6.14 | Контрольная работа №6 по теме «Тела вращения». |
|
|
| 7. Первообразная и интеграл (15 ч) |
| 87 | 7.1 | Работа над ошибками. Первообразная. |
|
|
| 88 | 7.2 | Решение задач по теме «Первообразная». |
|
|
| 89 | 7.3 | Правила нахождения первообразных. |
|
|
| 90 | 7.4 | Использование правил нахождения первообразных. |
|
|
| 91 | 7.5 | Площадь криволинейной трапеции и интеграл. |
|
|
| 92 | 7.6 | Вычисление интегралов. |
|
|
| 93 | 7.7 | Площадь криволинейной трапеции и интеграл. Вычисление интегралов. |
|
|
| 94 | 7.8 | Вычисление площадей с помощью интегралов. |
|
|
| 95 | 7.9 | Решение задач на вычисление площадей с помощью интегралов. |
|
|
| 96 | 7.10 | Вычисление площадей. |
|
|
| 97 | 7.11 | Применение интегралов для решения физических задач. |
|
|
| 98 | 7.12 | Простейшие дифференциальные уравнения. |
|
|
| 99 | 7.13 | Решение задач по теме «Интеграл». |
|
|
| 100 | 7.14 | Урок обобщения и систематизации знаний по теме «Интеграл». |
|
|
| 101 | 7.15 | Контрольная работа №7 по теме «Интеграл». |
|
|
| 8. Объёмы тел (22 ч) |
| 102 | 8.1 | Работа над ошибками. Понятие объёма. Объём прямоугольного параллелепипеда. |
|
|
| 103 | 8.2 | Решение задач по теме «Объём прямоугольного параллелепипеда». |
|
|
| 104 | 8.3 | Самостоятельная работа по теме «Объём прямоугольного параллелепипеда». |
|
|
| 105 | 8.4 | Объём прямой призмы. |
|
|
| 106 | 8.5 | Объём цилиндра. |
|
|
| 107 | 8.6 | Решение задач на вычисление объёмов прямой призмы и цилиндра. |
|
|
| 108 | 8.7 | Вычисление объёмов тел с помощью определённого интеграла. |
|
|
| 109 | 8.8 | Объём наклонной призмы. |
|
|
| 110 | 8.9 | Объём пирамиды. |
|
|
| 111 | 8.10 | Решение задач на вычисление объёма пирамиды. |
|
|
| 112 | 8.11 | Объём усечённой пирамиды. |
|
|
| 113 | 8.12 | Объём конуса. |
|
|
| 114 | 8.13 | Объём усечённого конуса. |
|
|
| 115 | 8.14 | Контрольная работа №8 по теме «Объёмы тел». |
|
|
| 116 | 8.15 | Работа над ошибками. Объём шара. |
|
|
| 117 | 8.16 | Решение задач по теме «Вычисление объёма шара». |
|
|
| 118 | 8.17 | Объёмы шарового сегмента, шарового слоя, шарового сектора. |
|
|
| 119 | 8.18 | Площадь сферы. |
|
|
| 120 | 8.19 | Решение задач на вычисление площади сферы. |
|
|
| 121 | 8.20 | Повторительно-обобщающий урок по теме «Объём шара и площадь сферы». |
|
|
| 122 | 8.21 | Контрольная работа №9 по теме «Шар и сфера». |
|
|
| 123 | 8.22 | Зачёт №3 по теме «Объёмы тел». |
|
|
|
|
| 9. Комбинаторика (9ч) |
|
|
| 124 | 9.1 | Работа над ошибками. Правило произведения. Размещения с повторениями. |
|
|
| 125 | 9.2 | Перестановки. |
|
|
| 126 | 9.3 | Решение заданий с использование перестановок. |
|
|
| 127 | 9.4 | Размещения без повторений. |
|
|
| 128 | 9.5 | Сочетания без повторений. |
|
|
| 129 | 9.6 | Бином Ньютона. |
|
|
| 130 | 9.7 | Сочетания без повторений и бином Ньютона. |
|
|
| 131 | 9.8 | Урок обобщения и систематизации знаний по теме «Комбинаторика». |
|
|
| 132 | 9.9 | Контрольная работа №10 по теме «Комбинаторика». |
|
|
| 10. Элементы теории вероятностей (8ч) |
| 133 | 10.1 | Работа над ошибками. Вероятность события. |
|
|
| 134 | 10.2 | Сложение вероятностей. |
|
|
| 135 | 10.3 | Сложение вероятностей. Решение примеров. |
|
|
| 136 | 10.4 | Условная вероятность. Независимость событий. |
|
|
| 137 | 10.5 | Вероятность произведения независимых событий. |
|
|
| 138 | 10.6 | Формула Бернулли. |
|
|
| 139 | 10.7 | Урок обобщения и систематизации знаний по теме «Элементы теории вероятности». |
|
|
| 140 | 10.8 | Контрольная работа №11 по теме «Элементы теории вероятности». |
|
|
| 11. Комплексные числа (13ч) |
| 141 | 11.1 | Работа над ошибками. Определение комплексных чисел. |
|
|
| 142 | 11.2 | Определение комплексных чисел. Сложение и умножение комплексных чисел. |
|
|
| 143 | 11.3 | Комплексно сопряженные числа. Модуль комплексного числа. |
|
|
| 144 | 11.4 | Вычитание и деления комплексных чисел. |
|
|
| 145 | 11.5 | Геометрическая интерпретация комплексного числа. |
|
|
| 146 | 11.6 | Использование геометрической интерпретации комплексного числа. |
|
|
| 147 | 11.7 | Тригонометрическая форма комплексного числа. |
|
|
| 148 | 11.8 | Умножение и деление комплексного числа, записанного в тригонометрической форме. |
|
|
| 149 | 11.9 | Умножение и деление комплексного числа, записанного в тригонометрической форме. Формула Муавра. |
|
|
| 150 | 11.10 | Квадратное уравнение с комплексной переменной. |
|
|
| 151 | 11.11 | Извлечение корня из комплексного числа. Алгебраические уравнения. |
|
|
| 152 | 11.12 | Урок обобщения и систематизации знаний по теме «Комплексные числа». |
|
|
| 153 | 11.13 | Контрольная работа №12 по теме «Комплексные числа». |
|
|
|
|
| 12. Повторение курса алгебры и начал математического анализа (21ч) |
|
|
| 154 | 12.1 | Работа над ошибками. Решение уравнений с одним неизвестным методом разложения на множители и методом введения нового неизвестного. |
|
|
| 155 | 12.2 | Решение уравнений с одним неизвестным функционально-графическим методом и методом перехода от уравнения φ(f(x))= φ(g(x)) к уравнению f(x)= g(x). |
|
|
| 156 | 12.3 | Решение уравнений с одним неизвестным с применением нескольких методов. |
|
|
| 157 | 12.4 | Решение уравнений с одним неизвестным методом раскрытия модулей на промежутках. |
|
|
| 158 | 12.5 | Аналитические приёмы решения уравнений с двумя неизвестными. |
|
|
| 159 | 12.6 | Графические приёмы решения уравнений с двумя неизвестными. |
|
|
| 160 | 12.7 | Основные понятия, связанные с решением неравенств с одним неизвестным. Решение алгебраических неравенств с одним неизвестным. |
|
|
| 161 | 12.8 | Решение показательных неравенств с одним неизвестным. |
|
|
| 162 | 12.9 | Решение логарифмических неравенств с одним неизвестным. |
|
|
| 163 | 12.10 | Решение систем уравнений с двумя неизвестными методами сложения и подстановки. |
|
|
| 164 | 12.11 | Решение систем уравнений с двумя неизвестными методам равносильных преобразований. |
|
|
| 165 | 12.12 | Решение систем уравнений с двумя неизвестными функционально-графическим методом. |
|
|
| 166 | 12.13 | Изображение на координатной плоскости решений неравенств и систем неравенств с двумя неизвестными. |
|
|
| 167 | 12.14 | Изображение на координатной плоскости решений неравенств и систем неравенств с двумя неизвестными. |
|
|
| 168 | 12.15 | Подходы к решению задач с параметрами. |
|
|
| 169 | 12.16 | Решение задач с параметрами графическим методом. |
|
|
| 170 | 12.17 | Решение задач с параметрами аналитическим методом. |
|
|
| 171 | 12.18 | Решение задач с параметрами. |
|
|
| 172 | 12.19 | Самостоятельная работа по теме «Решение задач с параметрами». |
|
|
| 173 | 12.20 | Урок обобщения и систематизации знаний по теме «Уравнения и неравенства с двумя переменными». |
|
|
| 174 | 12.21 | Контрольная работа №13 по теме «Уравнения и неравенства с одной и двумя переменными. Задачи с параметром». |
|
|
| 13.Повторение курса стереометрии 10-11 классов (17 ч) |
| 175 | 13.1 | Работа над ошибками. Аксиомы стереометрии и их следствия. Решение задач. |
|
|
| 176 | 13.2 | Параллельность прямых, прямой и плоскости. Решение задач. |
|
|
| 177 | 13.3 | Угол между прямыми. Решение задач. |
|
|
| 178 | 13.4 | Параллельность плоскостей. Решение задач. |
|
|
| 179 | 13.5 | Построение сечений в тетраэдре и параллелепипеде. |
|
|
| 180 | 13.6 | Теорема о трёх перпендикулярах. Решение задач. |
|
|
| 181 | 13.7 | Площадь поверхности и объём призмы. Решение задач. |
|
|
| 182 | 13.8 | Площадь поверхности и объём пирамиды. Решение задач. |
|
|
| 183 | 13.9 | Площадь поверхности и объём цилиндра. Решение задач. |
|
|
| 184 | 13.10 | Площадь поверхности и объём конуса. Решение задач. |
|
|
| 185 | 13.11 | Площадь поверхности сферы и объём шара. Решение задач. |
|
|
| 186 | 13.12 | Векторы в пространстве. Решение задач. |
|
|
| 187 | 13.13 | Метод координат в пространстве. Решение задач. |
|
|
| 188 | 13.14 | Конус. Решение задач ЕГЭ. |
|
|
| 189 | 13.15 | Цилиндр. Решение задач ЕГЭ. |
|
|
| 190 | 13.16 | Пирамида. Решение задач ЕГЭ. |
|
|
| 191 | 13.17 | Решение задач ЕГЭ. |
|
|
| 14.Итоговое повторение курса математики (13ч) |
| 192 | 13.1 | Степени и корни. |
|
|
| 193 | 13.2 | Преобразование логарифмических выражений. |
|
|
| 194 | 13.3 | Преобразование тригонометрических выражений. |
|
|
| 195 | 13.4 | Решение тригонометрических уравнений, сводящихся к квадратным, однородных, линейных относительно 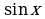 и и 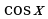 |
|
|
| 196 | 13.5 | Решение иррациональных уравнений. |
|
|
| 197 | 13.6 | Уравнение касательной к графику функции. Применение производной для исследования функций. |
|
|
| 198 | 13.7 | Первообразная. |
|
|
| 199 | 13.8 | Интеграл. |
|
|
| 200 | 13.9 | Повторение. Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке. |
|
|
| 201 | 13.10 | Повторение. Текстовые задачи. |
|
|
| 202 | 13.11 | Решение текстовых задач. |
|
|
| 203 | 13.12 | Итоговая контрольная работа за курс средней школы. |
|
|
| 204 | 13.13 | Подведение итогов. |
|
|





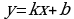 или совпадает с ней;
или совпадает с ней;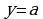 или совпадает с ней;
или совпадает с ней;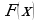 есть первообразная функции
есть первообразная функции 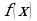 ;
;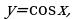 ее свойства и график.
ее свойства и график.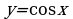 . Графическое решение тригонометрических уравнений и неравенств.
. Графическое решение тригонометрических уравнений и неравенств.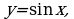 ее свойства и график.
ее свойства и график.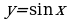 . Графическое решение тригонометрических уравнений и неравенств.
. Графическое решение тригонометрических уравнений и неравенств.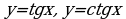 их свойства и графики.
их свойства и графики.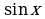 и
и