Решение дифференциальных уравнений I и II порядков.

Практическое занятие: Решение дифференциальных уравнений I и II порядков

Что нужно знать и уметь, для того чтобы научиться решать дифференциальные уравнения? Для успешного изучения дифференциальных уравнений вы должны хорошо уметь интегрировать и дифференцировать. Чем качественнее изучены темы "Производная функции" и "Неопределенный интеграл", тем будет легче разобраться в дифференциальных уравнениях. Придётся много интегрировать. И дифференцировать.

1. Решение дифференциальных уравнений I порядка

ДУ I порядка в общем случае содержит:

1) независимую переменную х;

2) зависимую переменную (функцию) у;

3) первую производную функции: (или ).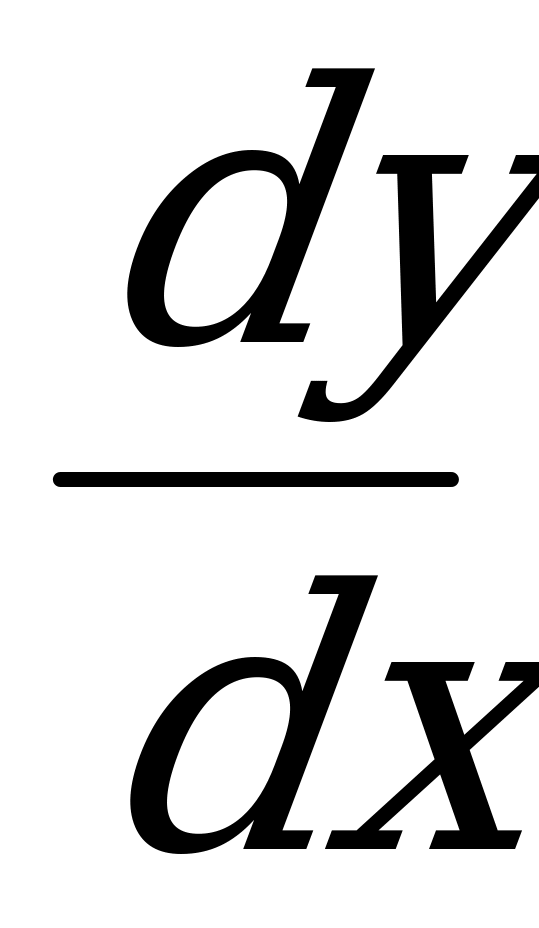

В некоторых уравнениях I порядка может отсутствовать «икс» или (и) «игрек», но это не существенно – важно чтобы в ДУ была первая производная , и не было производных высших порядков

Что значит решить дифференциальное уравнение? Решить дифференциальное уравнение – это значит, найти множество всех функций, которые удовлетворяют данному уравнению. Такое множество функций часто имеет вид 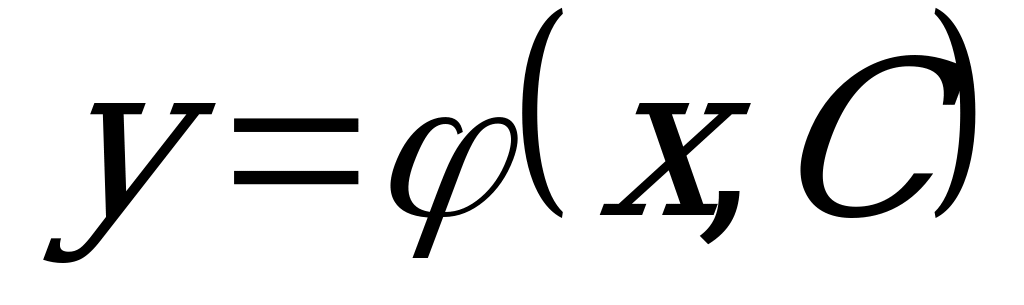(С – произвольная постоянная), который называется общим решением дифференциального уравнения.

Мы познакомились с двумя видами ДУ I порядка: уравнениями с разделяющимися переменными и линейными уравнениями. Вспомним как решают уравнения данных видов (при необходимости можно обратиться к предыдущей лекции). Перед решением уравнения следует определить его вид и, соответственно, метод решения.

Пример 1. Решить уравнение: .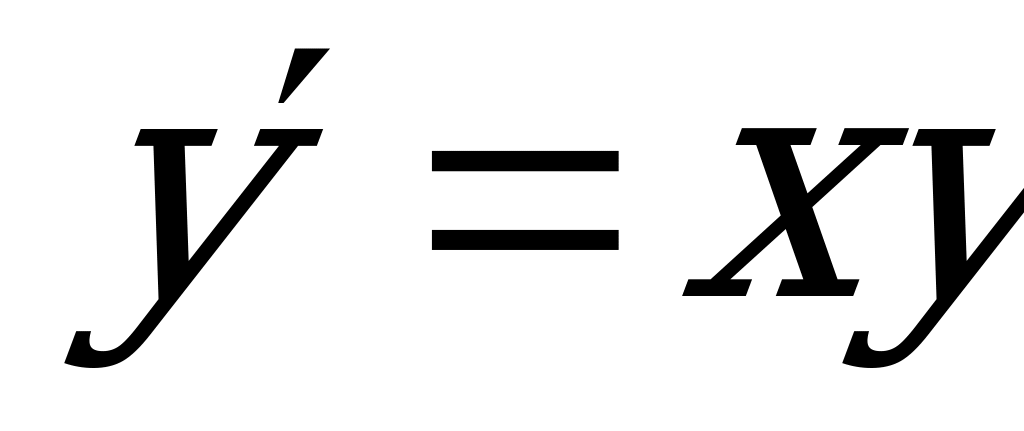

Решение:

Данное уравнение является ДУ с разделяющимися переменными. Работаем по алгоритму (приведен в лекции).

1) Разделяем переменные:

.

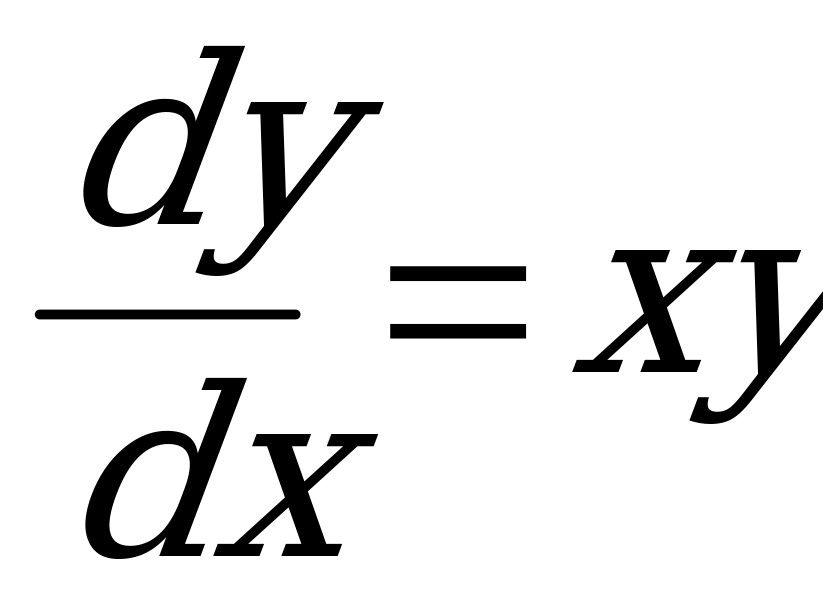
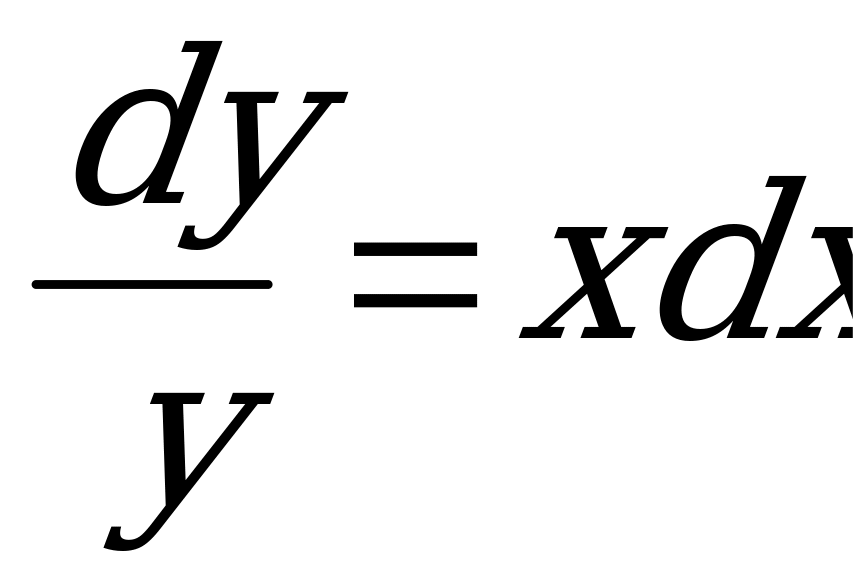2) Интегрируем обе части уравнения:

.

.

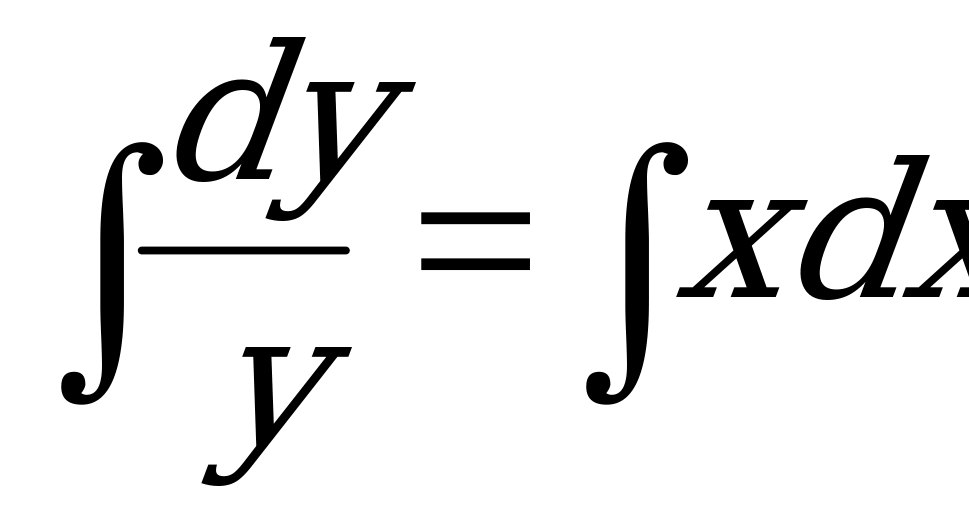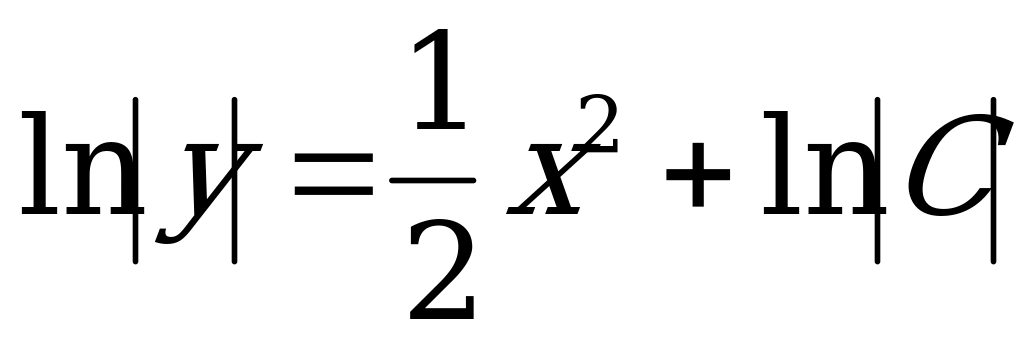Напоминаю, что если в решении содержится логарифм, то вместо постоянной интегрирования С записывают ее логарифм.

3) Преобразовываем выражение и выражаем у явно:

.

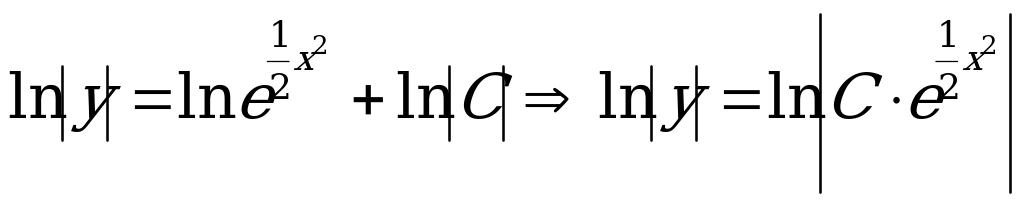При этом использовали свойство логарифмов .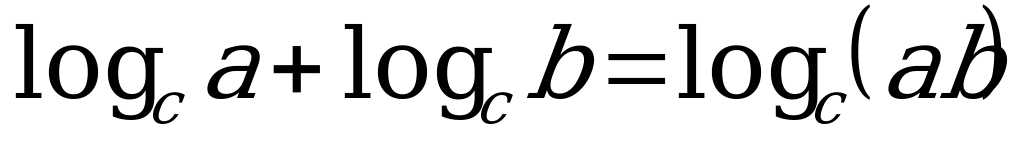

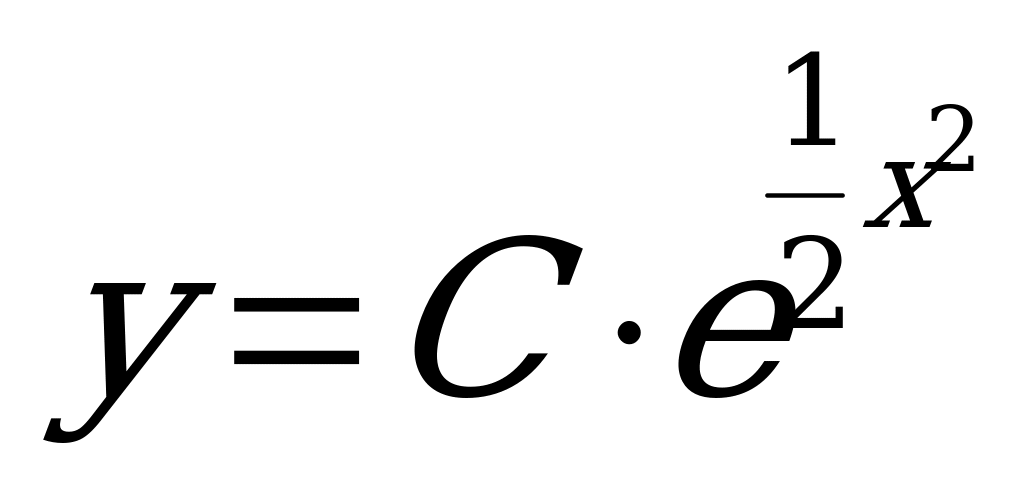- общее решение уравнения.

Ответ: .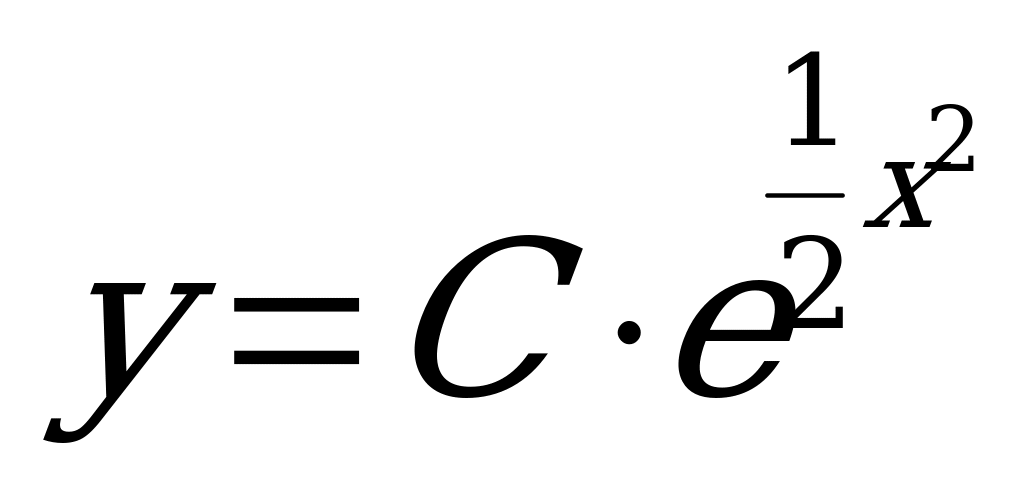

Пример 2. Решить уравнение: .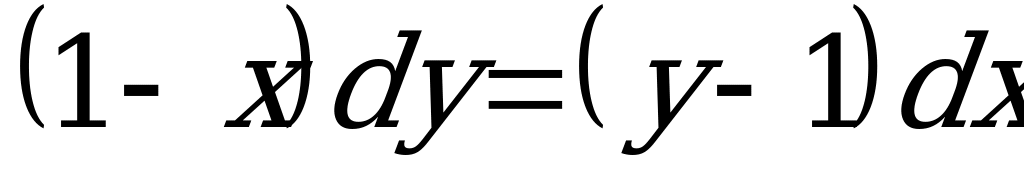

Решение:

Уравнение записано в дифференциалах и является ДУ с разделяющимися переменными. 1) Разделяем переменные:

.

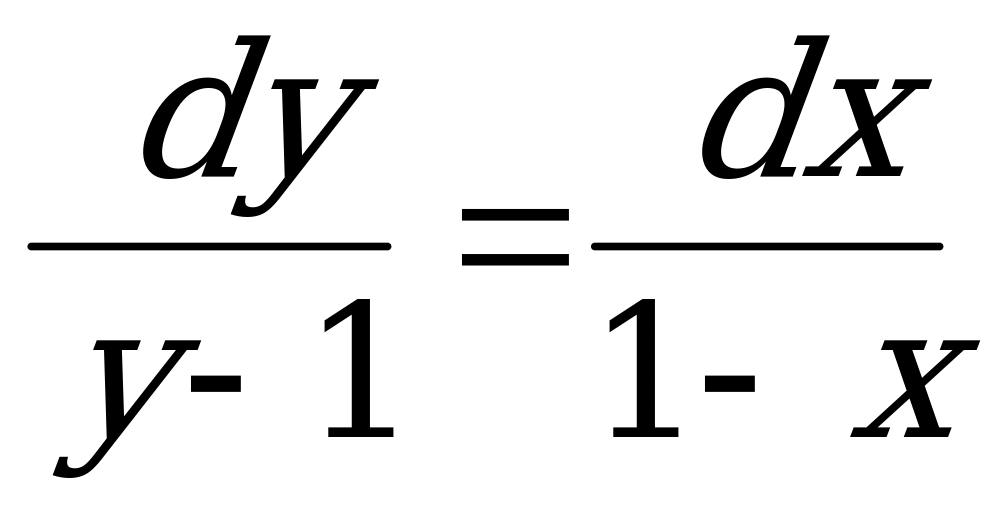2) Интегрируем обе части уравнения:

.

.

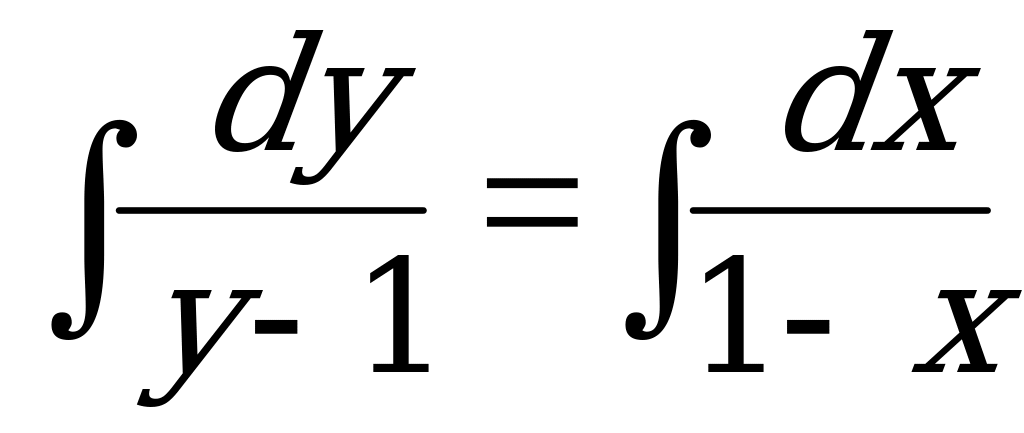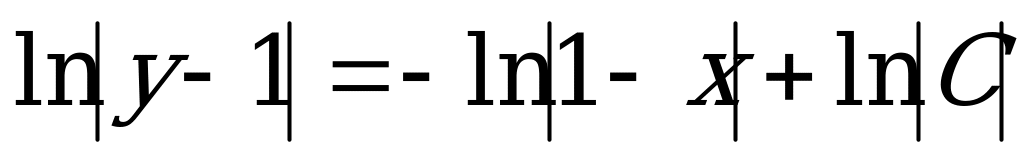3) Используя определение и свойства логарифма, выразим у:

.

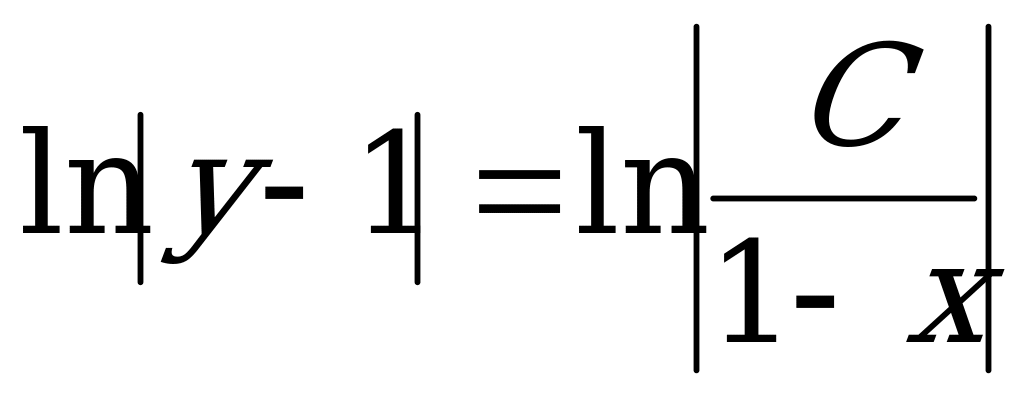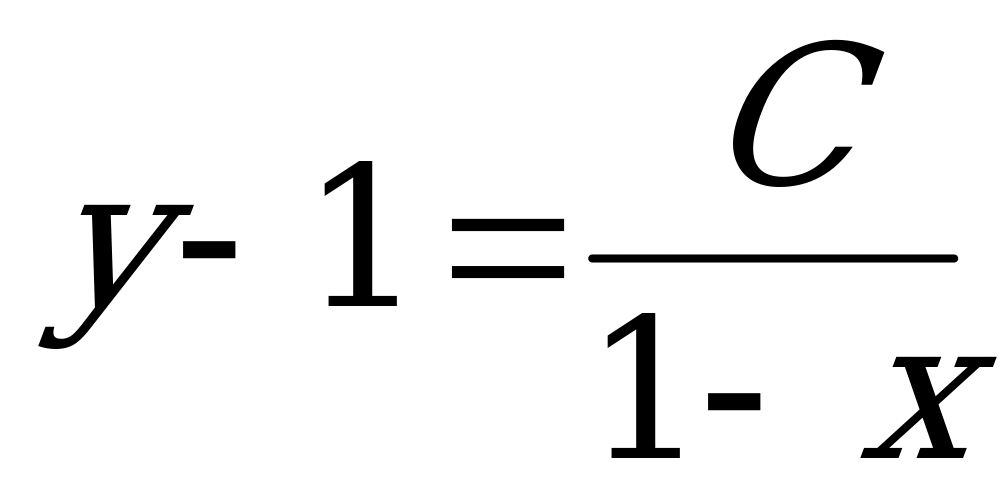или .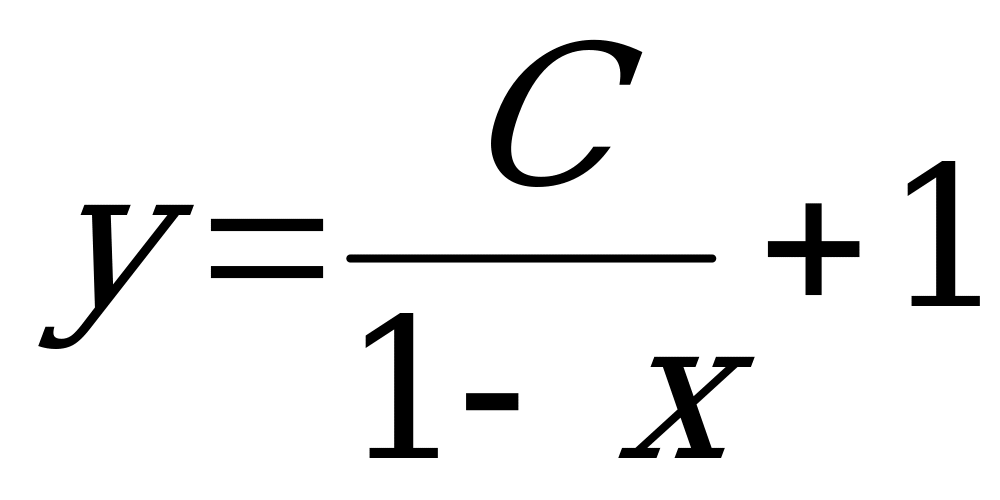

Ответ: .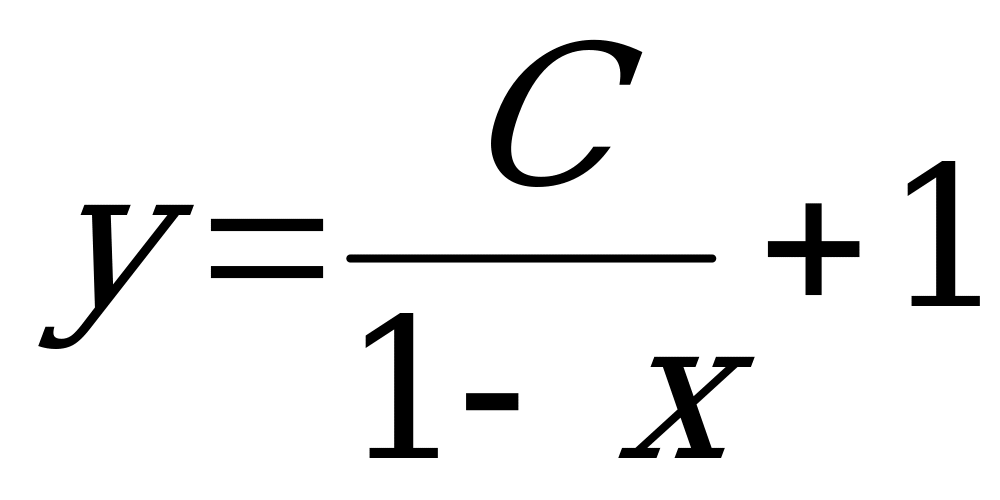

Пример 3. Решить уравнение: .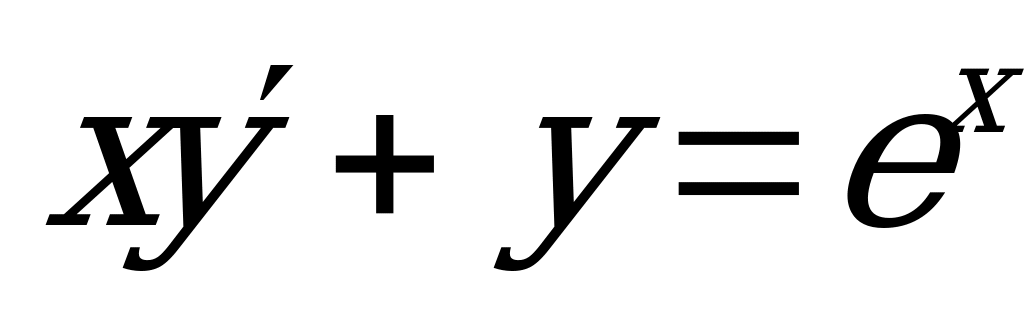

Решение:

1) Данное уравнение является линейным неоднородным ДУ I порядка.

Перепишем уравнение в стандартном виде:

; .

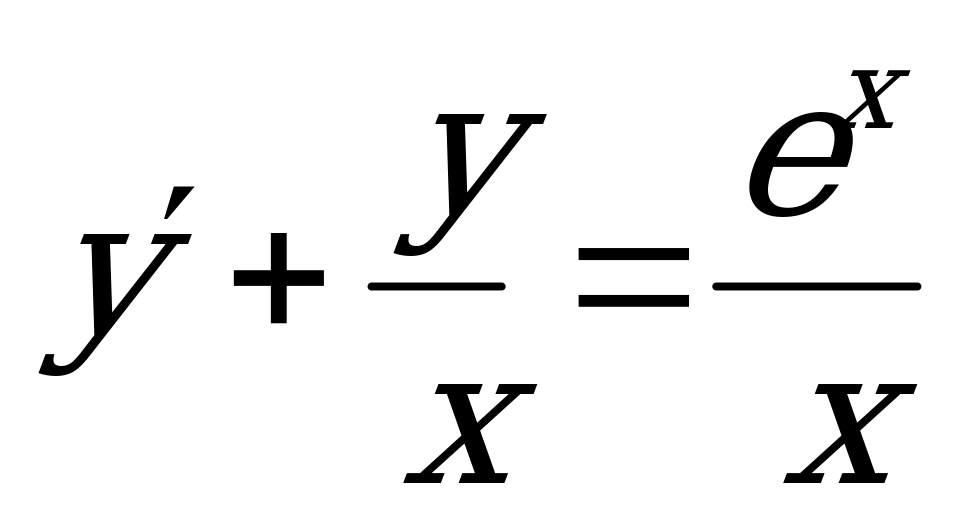
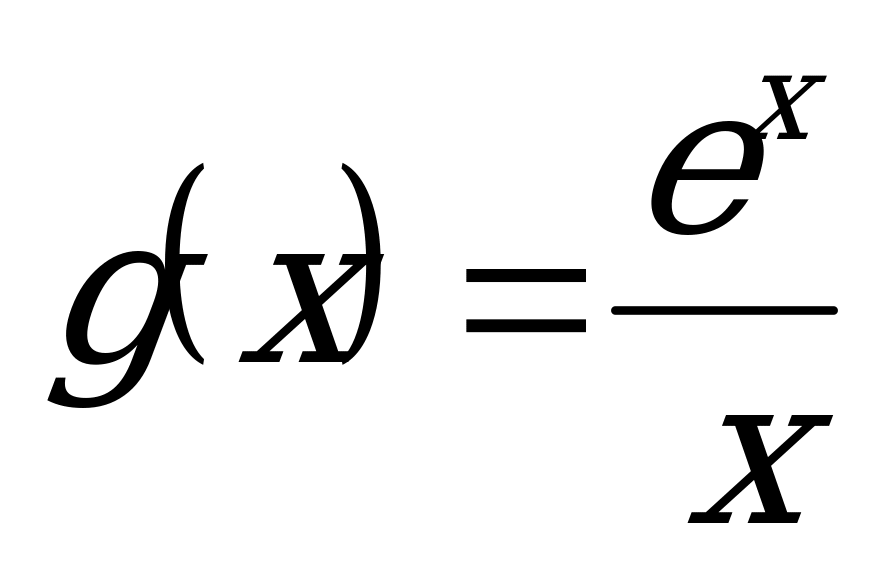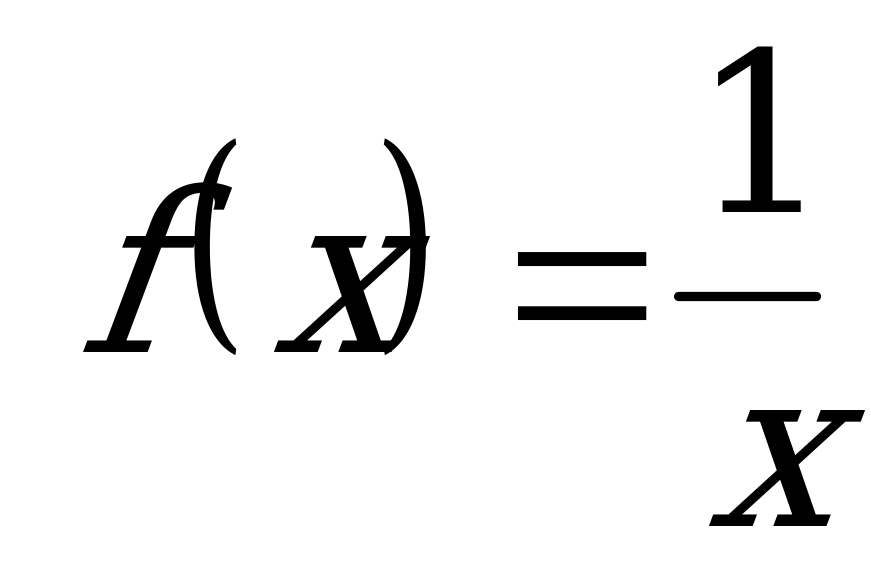2) Общее решение неоднородного линейного уравнения имеет вид:

.

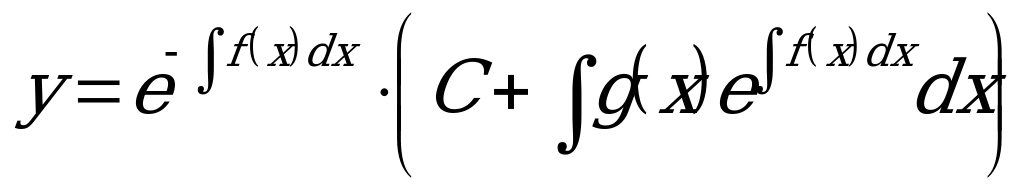Подставляя в это выражение значение функци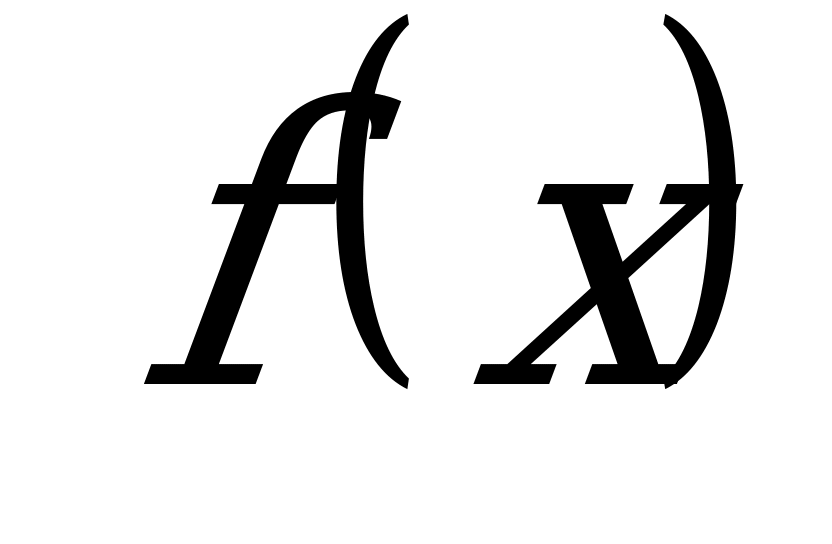й и 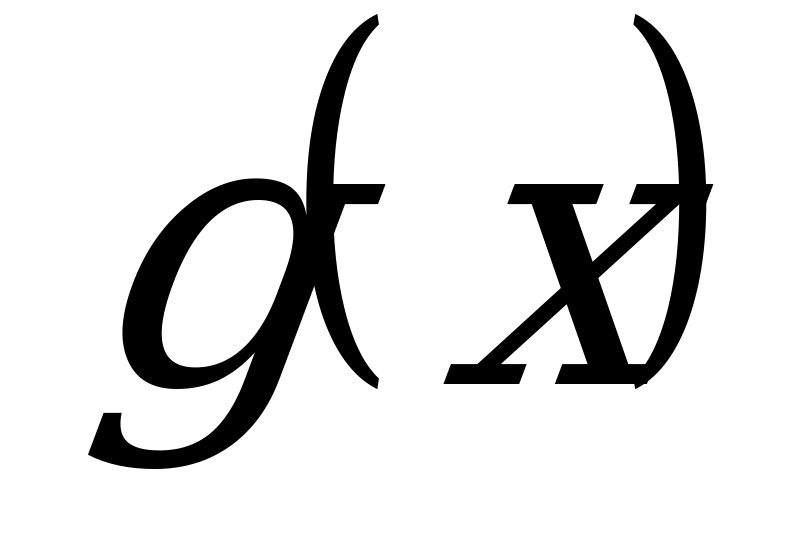, получим

.

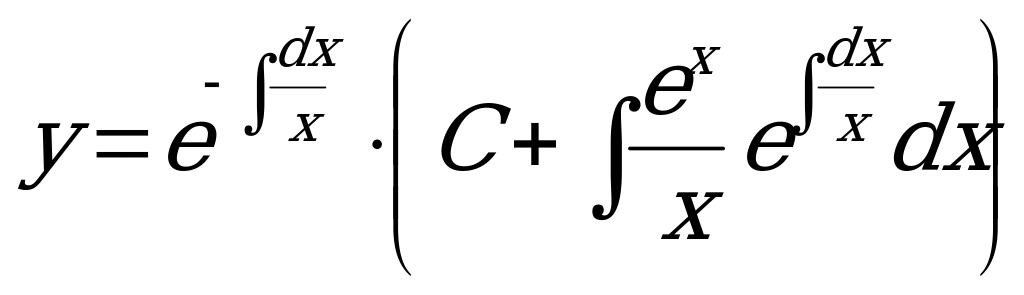Вычислим значения промежуточных интегралов:

; ; .

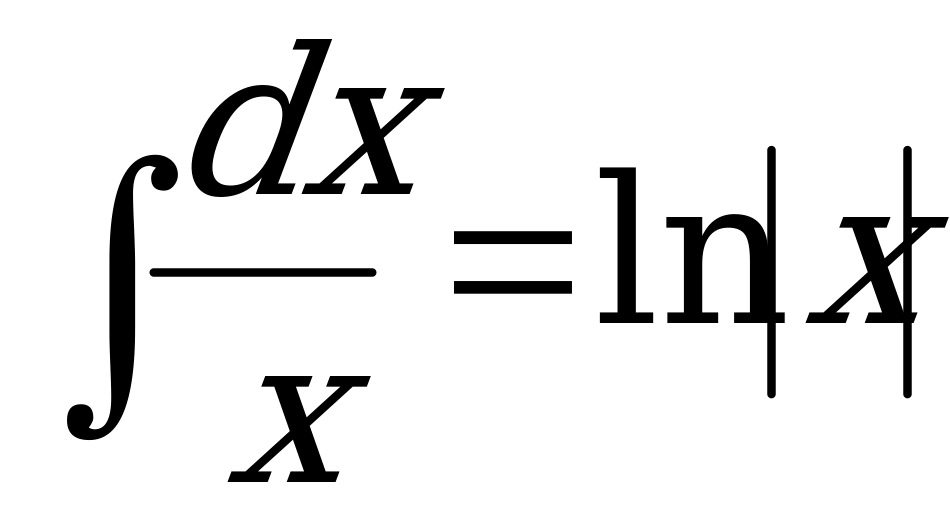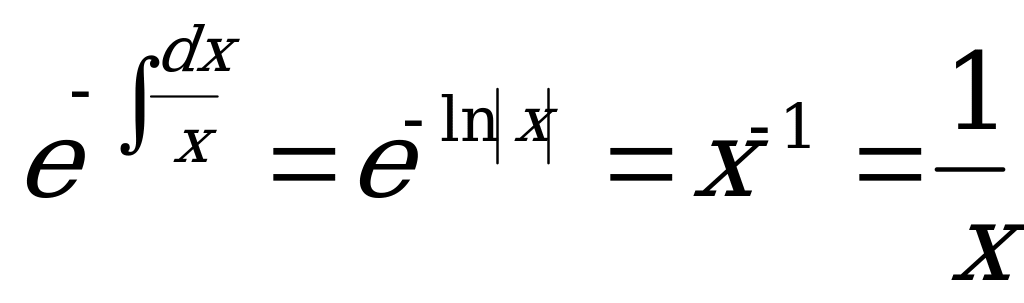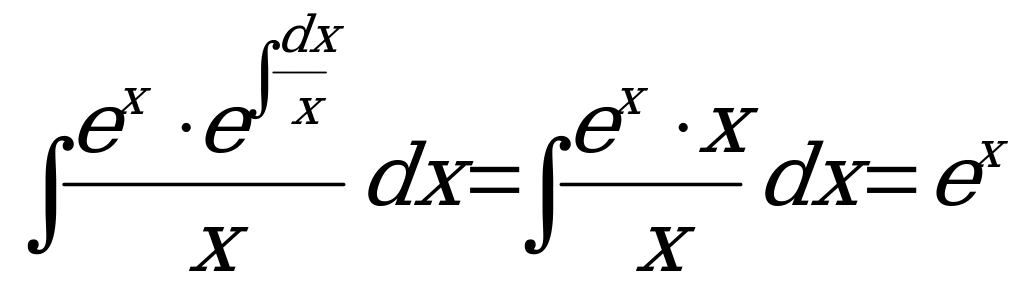Напоминаю, что при вычислении этих интегралов полагаем С=0, поскольку постоянная интегрирования уже включена в общий вид решения.

Запишем общее решение ДУ: .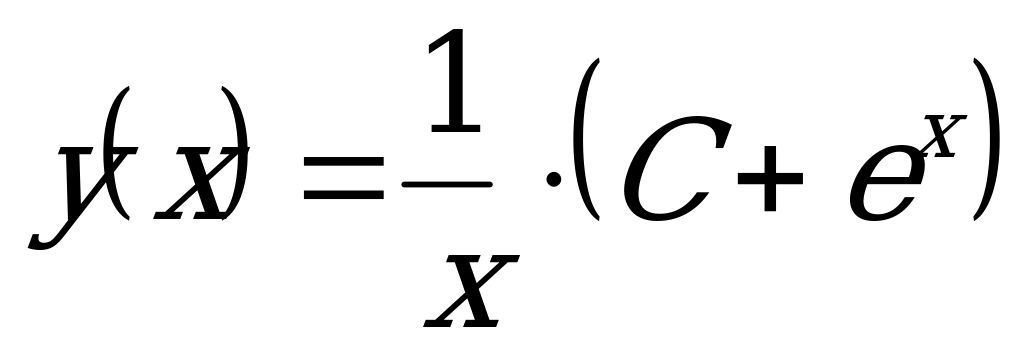

Ответ: .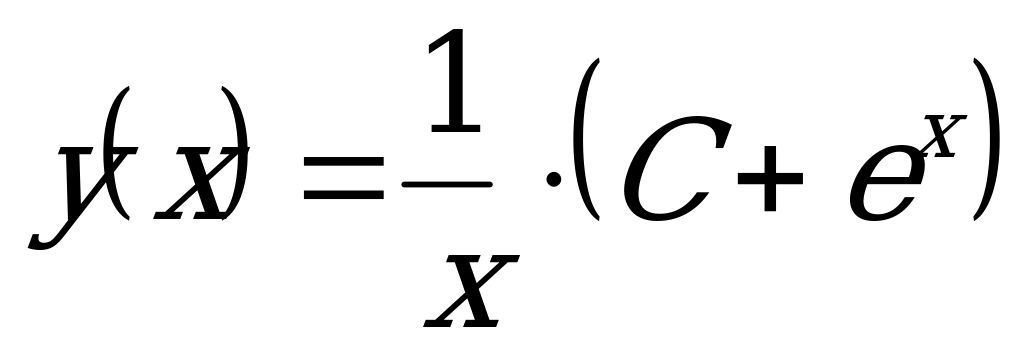

2. Решение дифференциальных уравнений II порядка

Переходим к рассмотрению дифференциальных уравнений второго порядка. У многих студентов может быть предубеждение, что ДУ II порядка –  что-то очень трудное и недоступное для освоения. Это не так. Научиться решать дифференциальные уравнения высшего порядка вряд ли сложнее, чем «обычные» ДУ I порядка. А местами – даже проще, поскольку в решениях активно используется материал школьной программы.

Наиболее популярны дифференциальные уравнения второго порядка. В дифференциальное уравнение второго порядка обязательно входит вторая производная и не входят производные более высоких порядков: 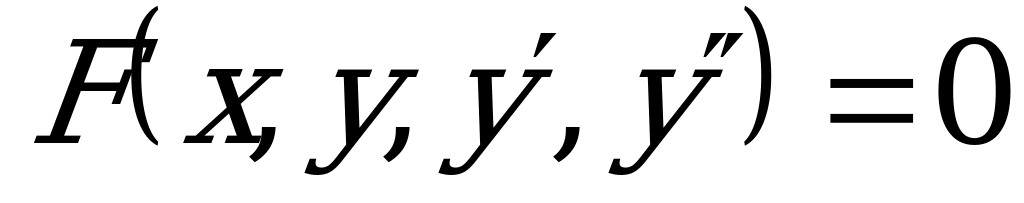. ДУ II порядка, которые предлагаются в практических задачах, можно разделить на две основные группы.

1) Первая группа – так называемые уравнения, допускающие понижение степени (порядка).

2) Вторая группа – линейные уравнения с постоянными коэффициентами.

ДУ II порядка, допускающее понижение степени решают двукратным интегрированием. Для решения однородного линейного уравнения с постоянными коэффициентами используют характеристическое уравнение, которое получают из исходного с помощью замены: 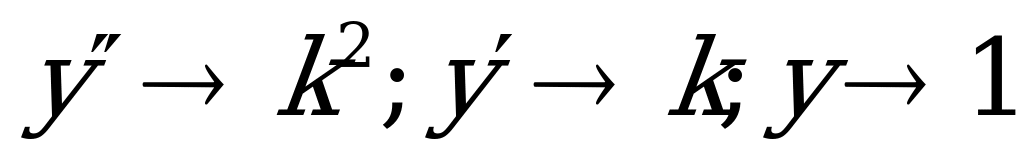: 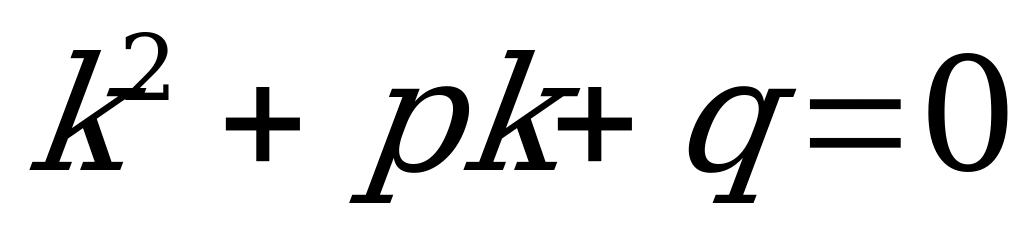. В зависимости от знака дискриминанта полученного характеристического уравнения общее решение ДУ записывается по разному:

а) Если , то характеристическое уравнение имеет два действительных корня: 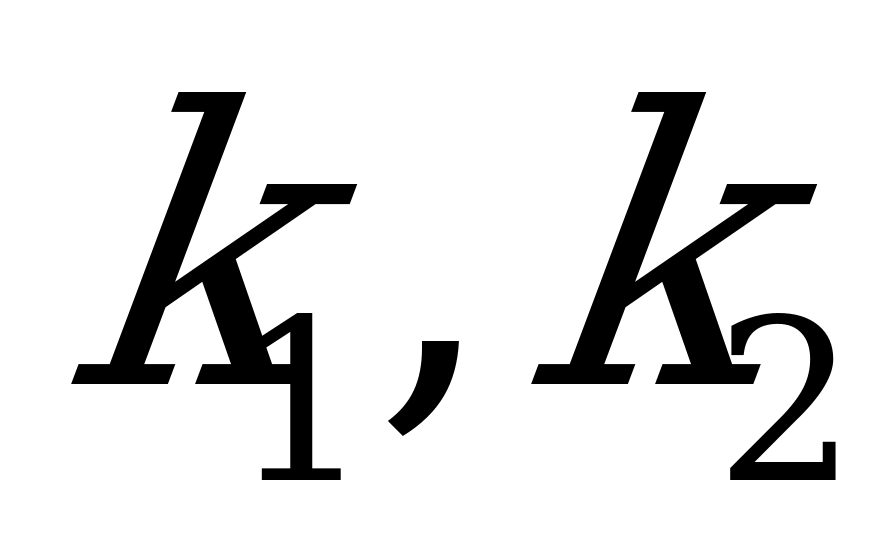. Тогда общее решение ДУ имеет вид: 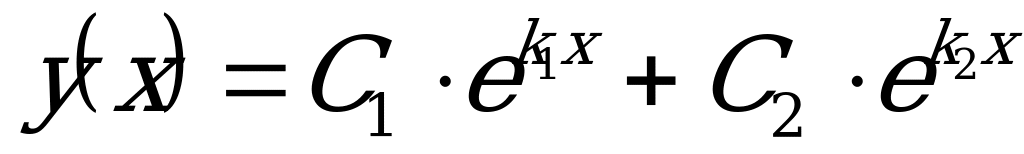, где 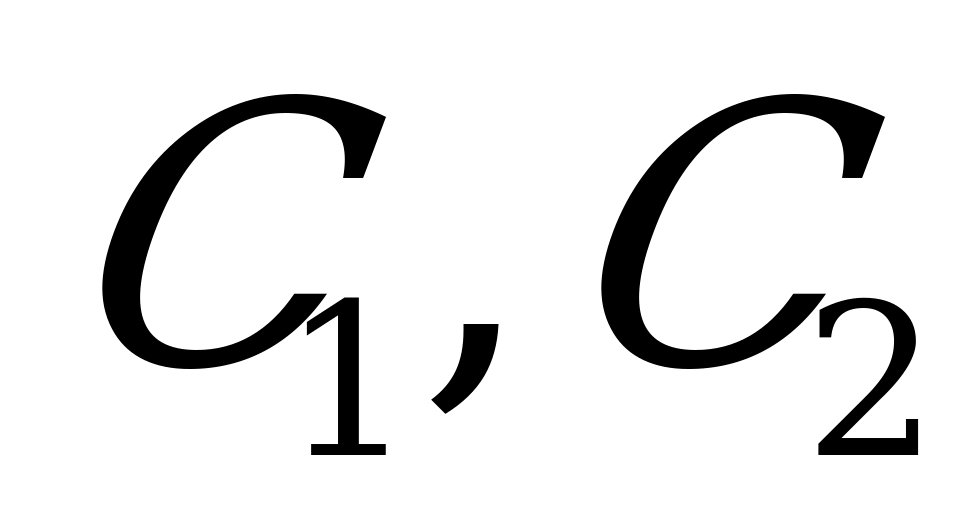- произвольные постоянные.

б) Если 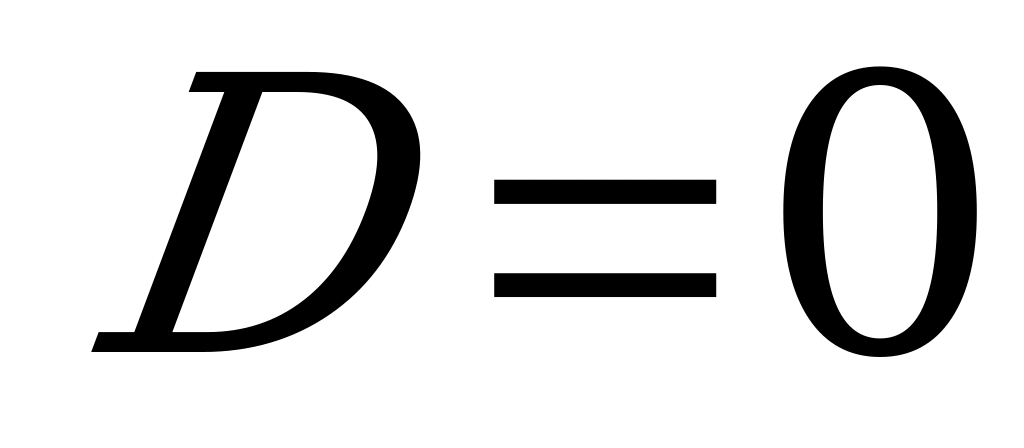, то характеристическое уравнение имеет один действительный корень: 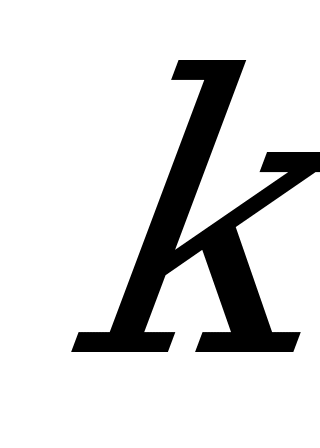. Тогда общее решение ДУ имеет вид: .

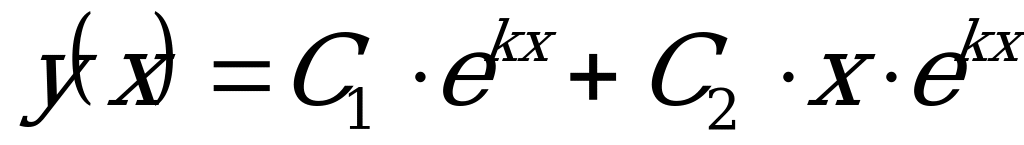в) Если 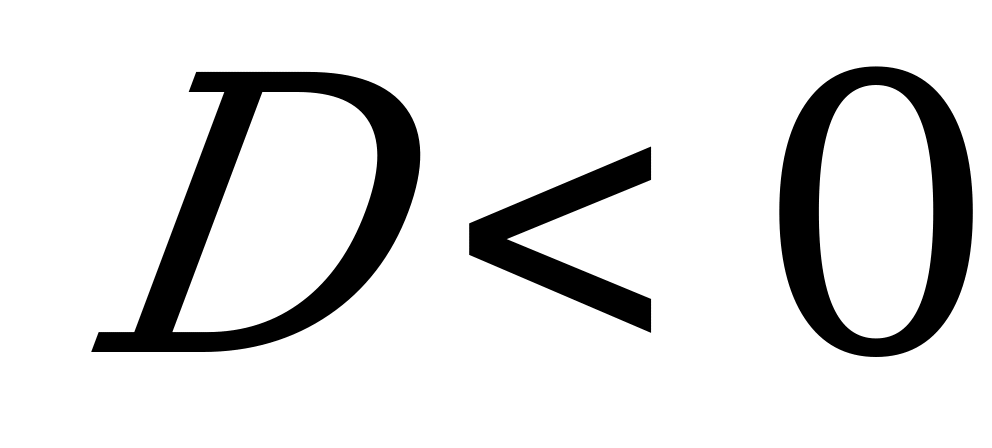, то характеристическое уравнение не имеет действительных корней. Общее решение ДУ в этом случае имеет вид: 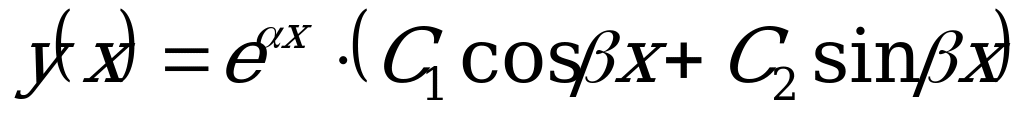, где .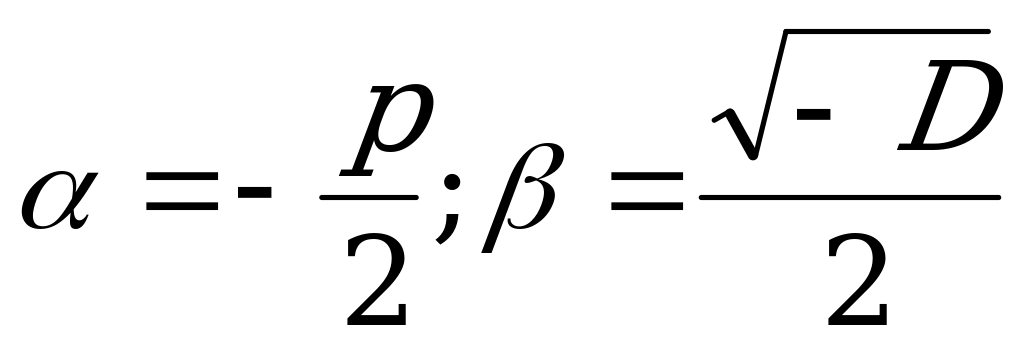

Пример 4. Решить уравнение: .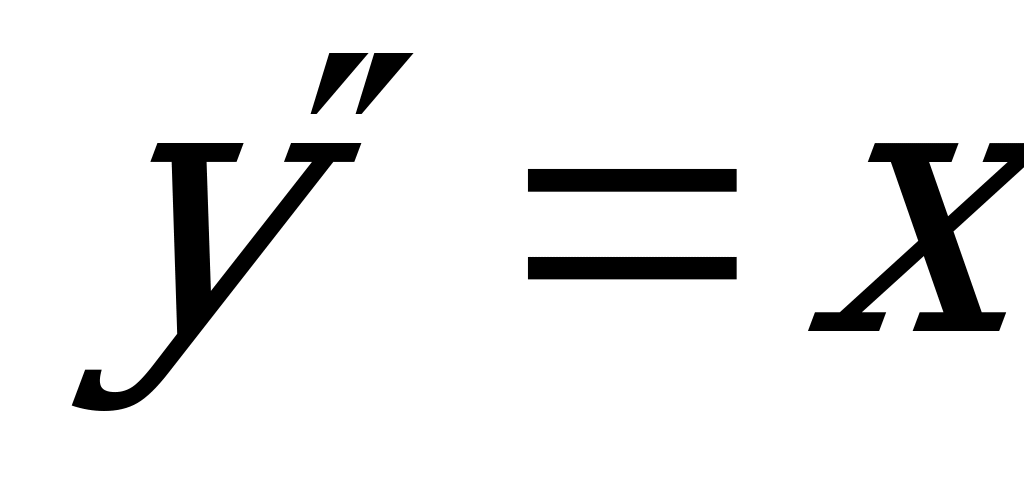

Решение:

Данное уравнение является простейшим ДУ II порядка, допускающим понижение степени.

1) Введем новую переменную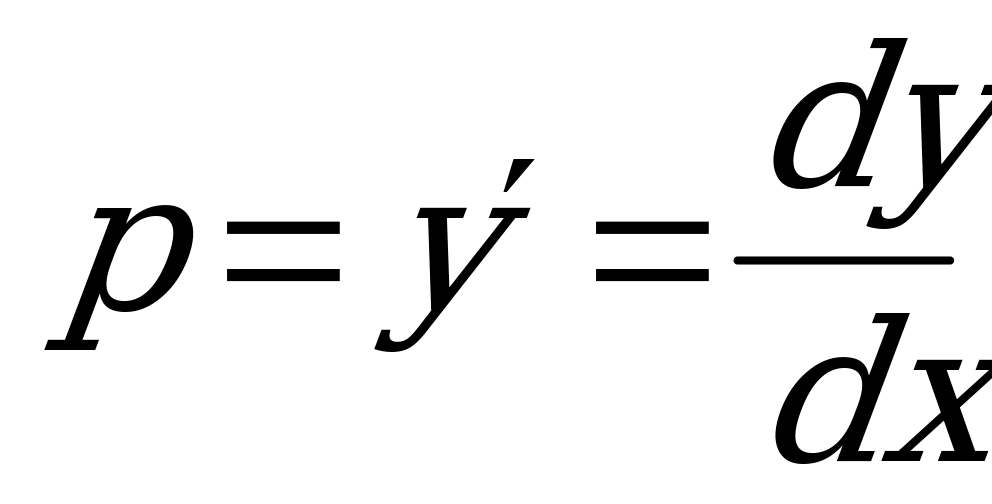

2) Получим ДУ I порядка с разделяющимися переменными: .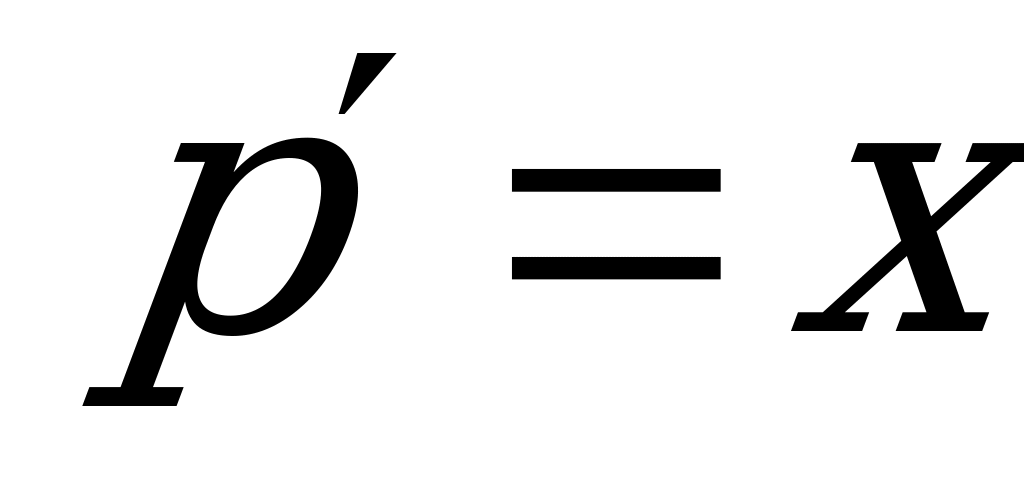

Перепишем уравнение в виде: .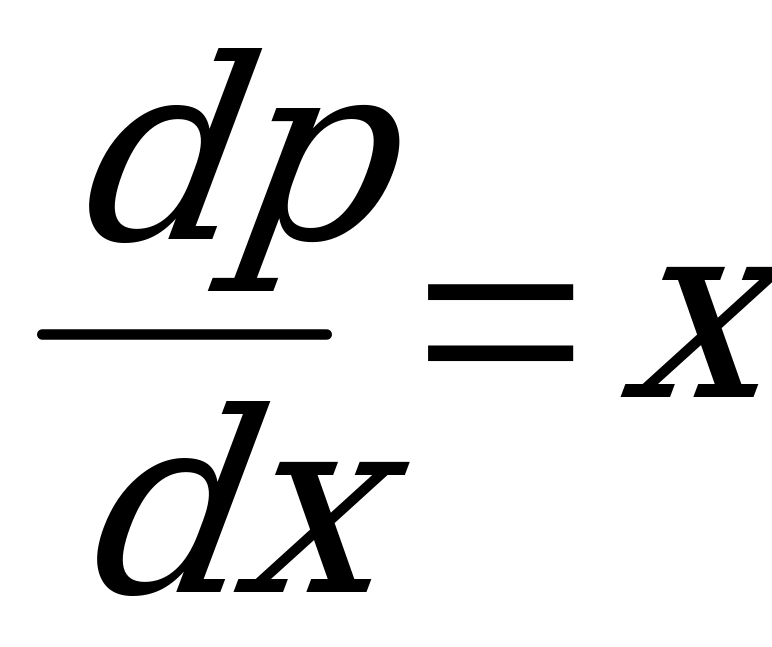

Разделим переменные : .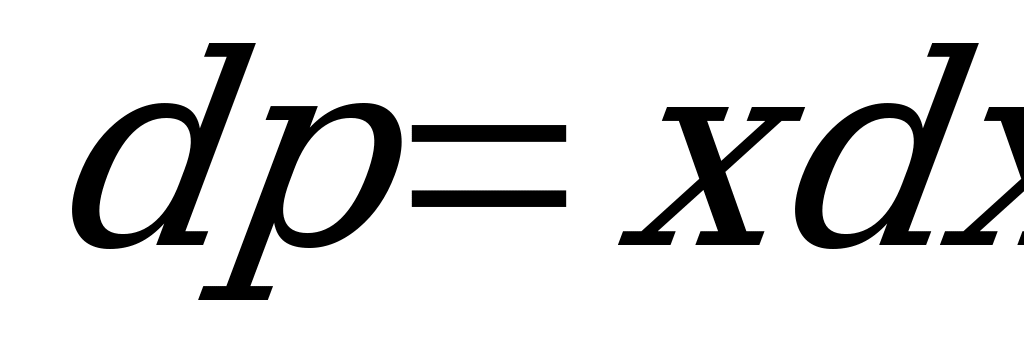

Проинтегрируем обе части полученного уравнения: .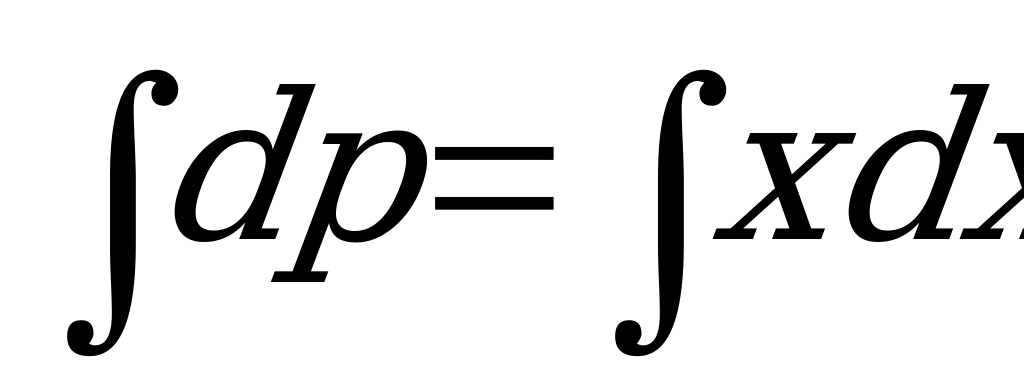

Получим .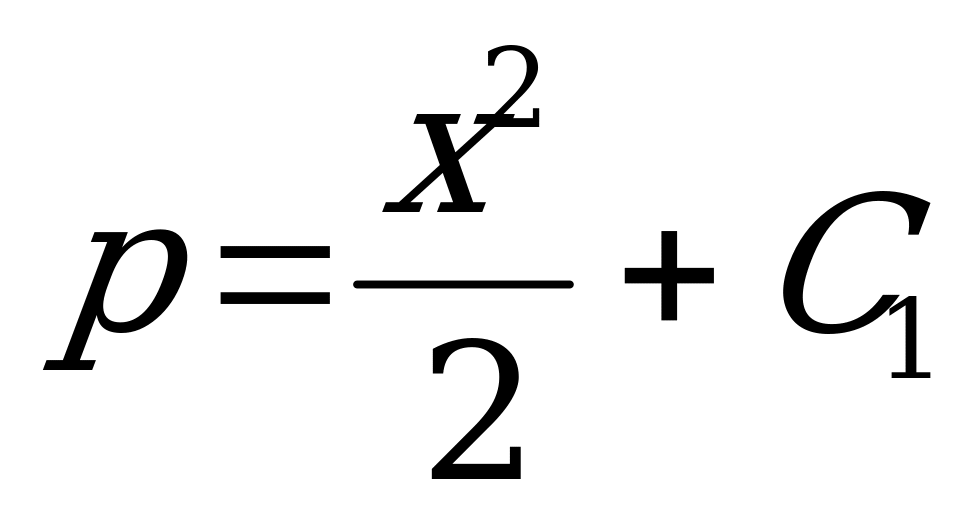

3) Вернемся к старой переменной и решим полученное уравнение: .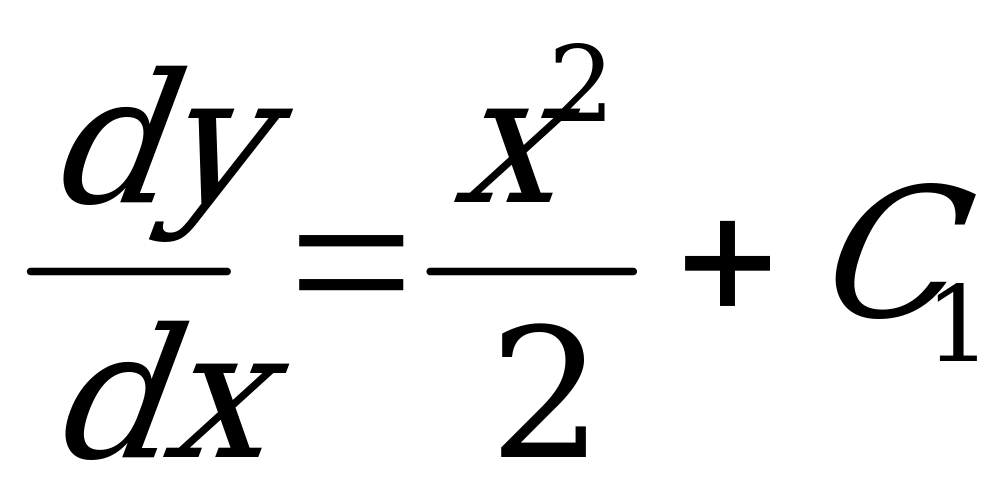

;

.

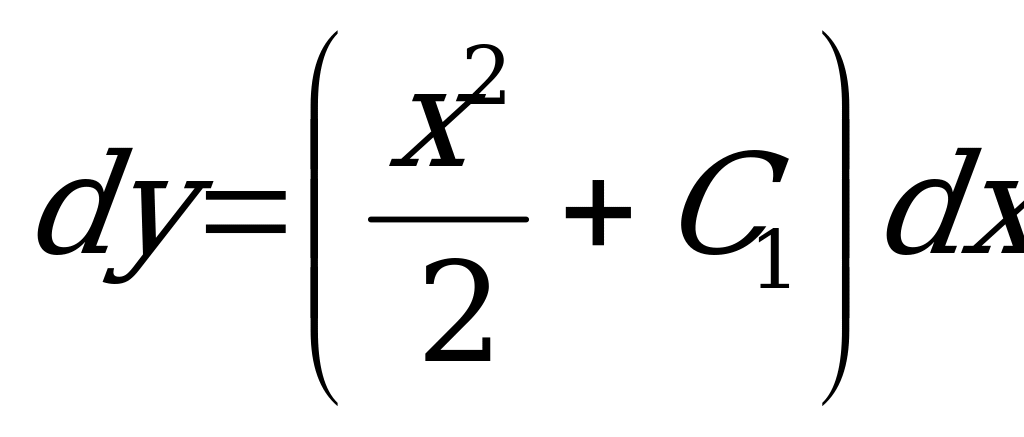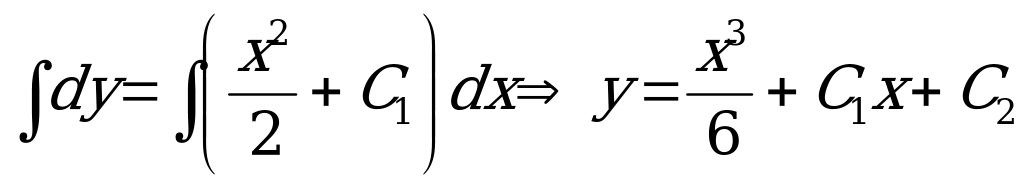Ответ: .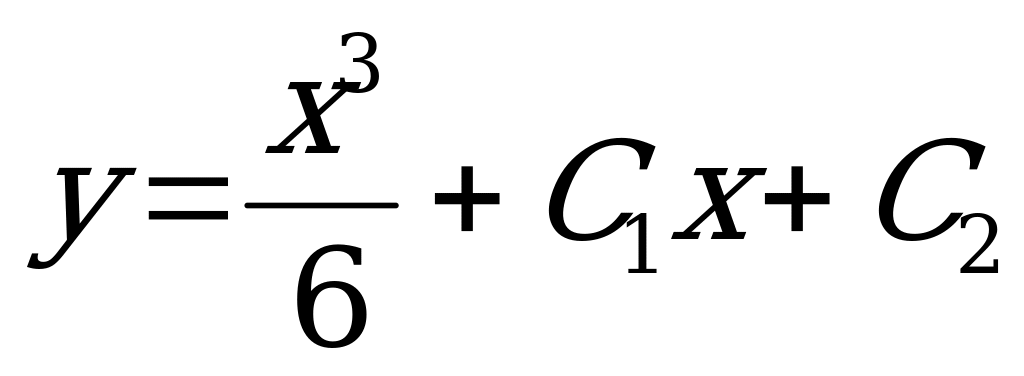

Пример 5. Решить уравнение: .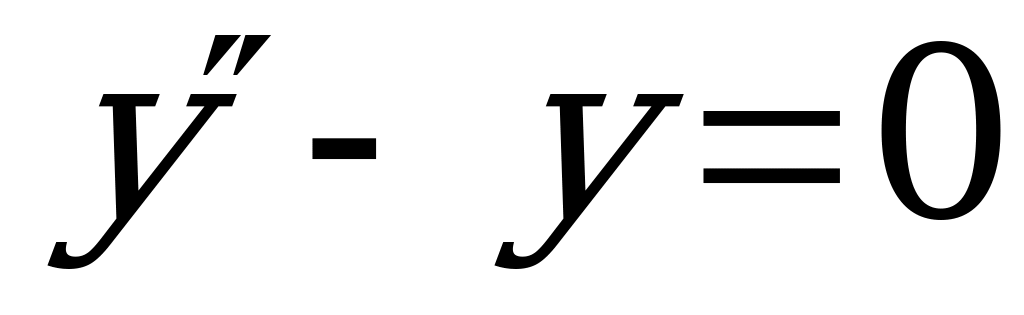

Решение:

Данное уравнение является однородным линейным ДУ II порядка с постоянными коэффициентами.

1) Составляем характеристическое уравнение, используя замену: :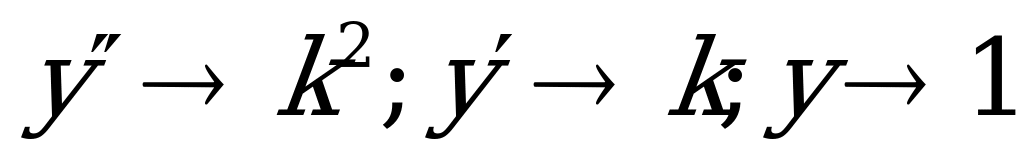

.

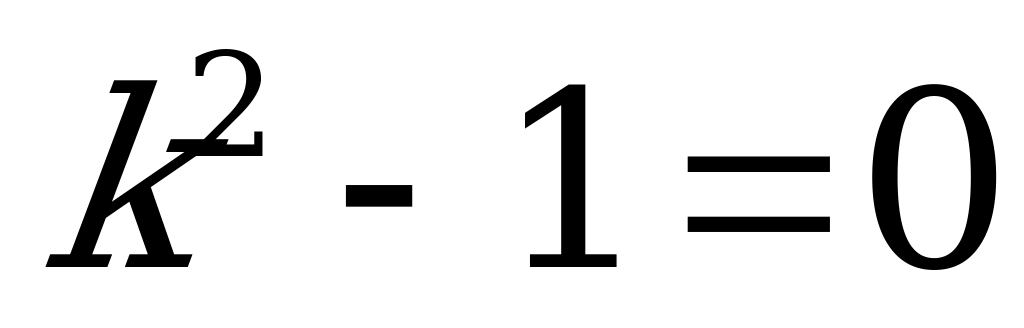2) Решаем полученное квадратное уравнение.

.

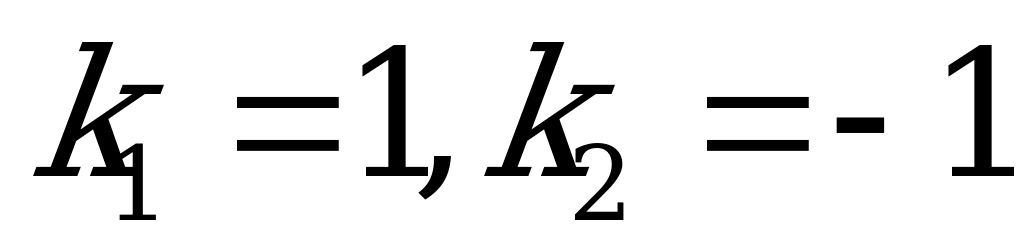Значит, общее решение ДУ имеет вид: .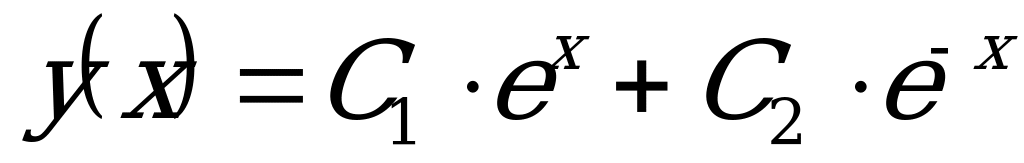

Ответ: .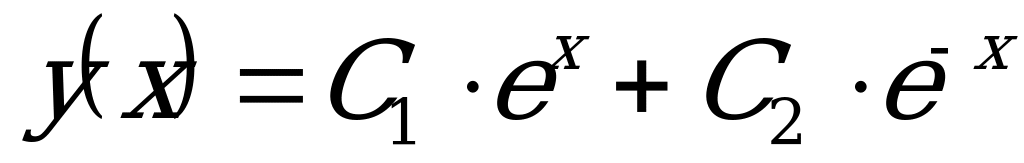

Задания для самостоятельного решения:

Решите ДУ I и II порядков. Полученные результаты сравните с ответом.

1. Уравнения с разделяющимися переменными:

1) 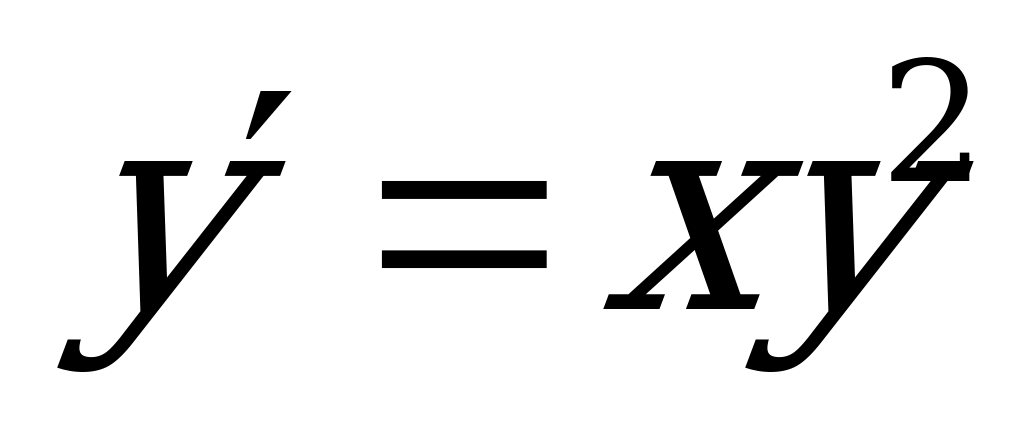(Ответ: )

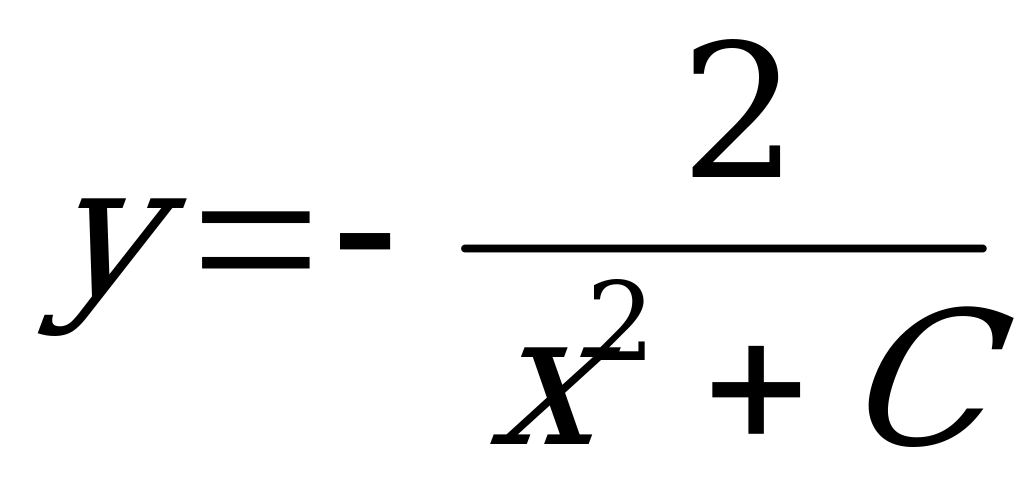2) 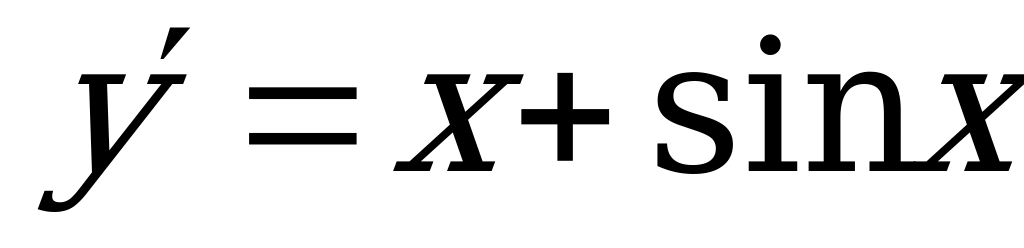(Ответ: )

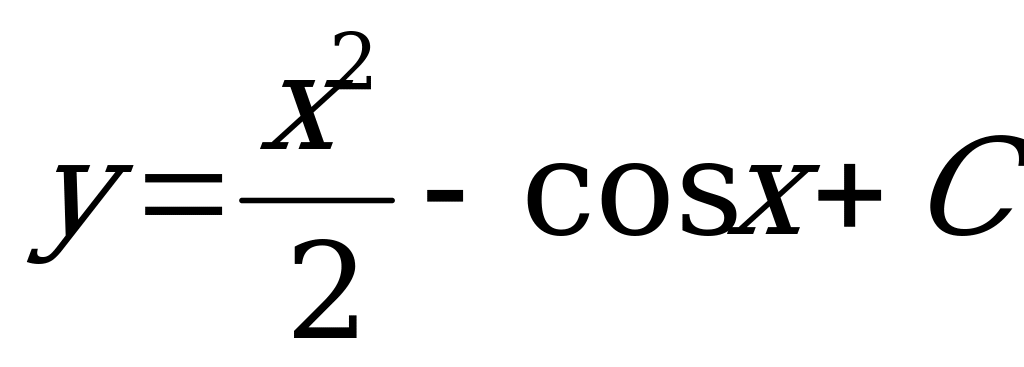3) 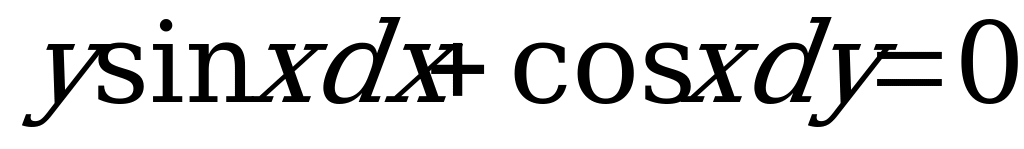(Ответ: )

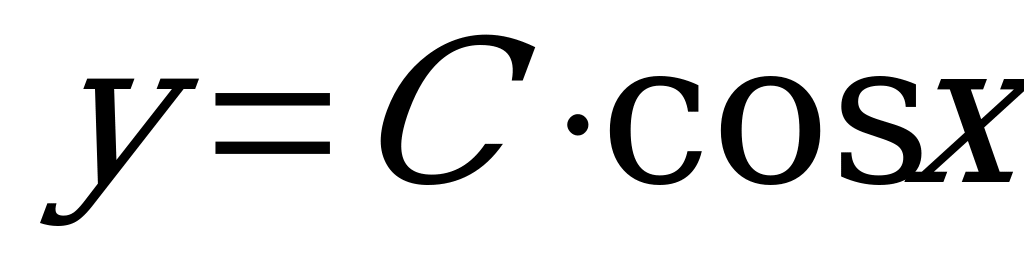4) 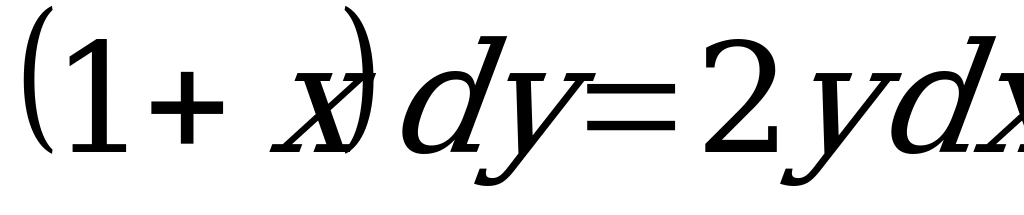(Ответ: )

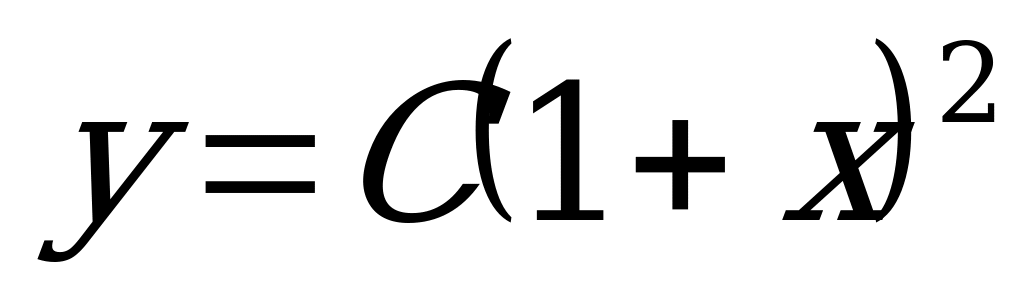2. Неоднородные линейные уравнения:

1) 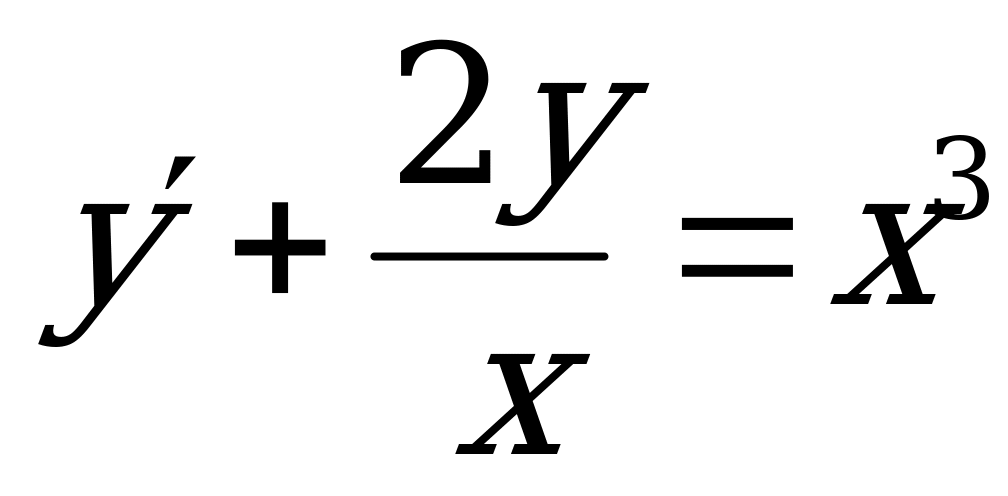(Ответ: )

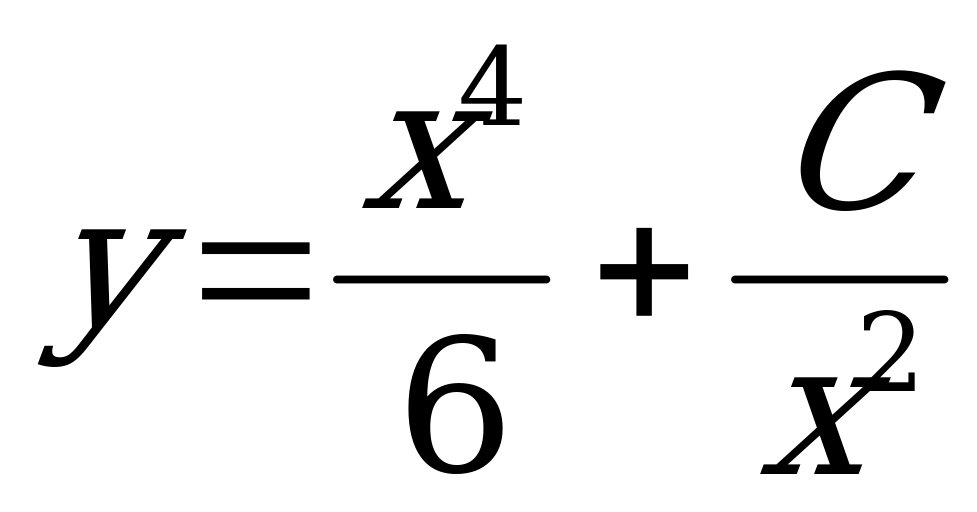2) 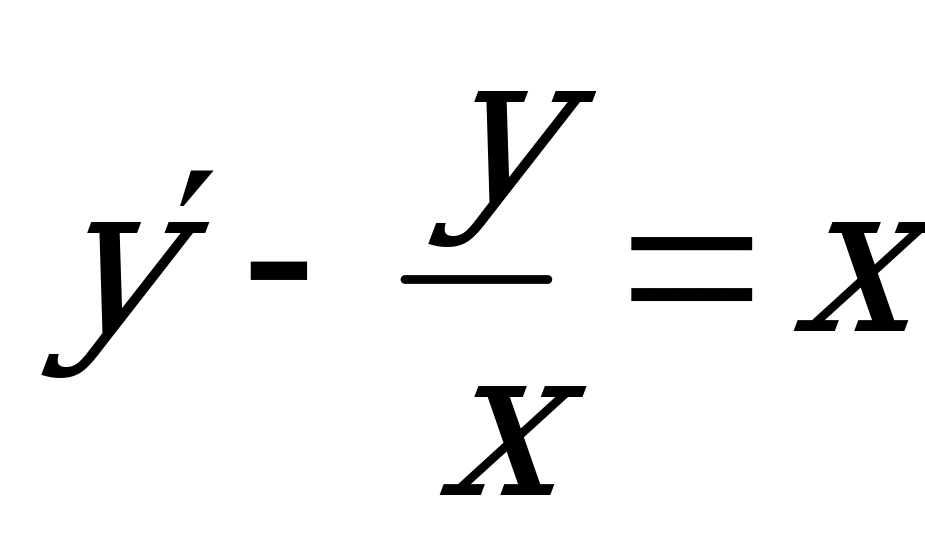(Ответ: )

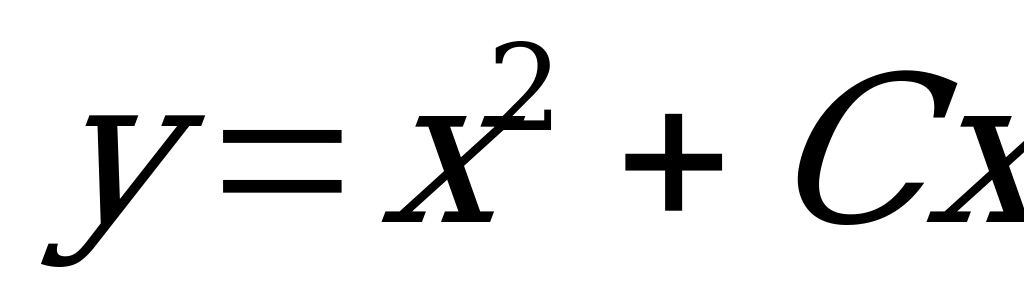3. ДУ II порядка, допускающие понижение степени:

1) 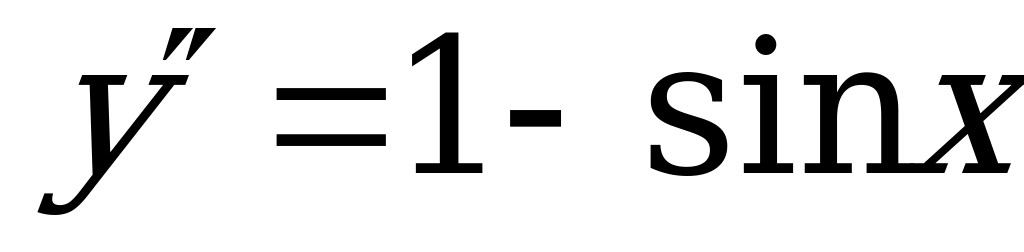(Ответ: )

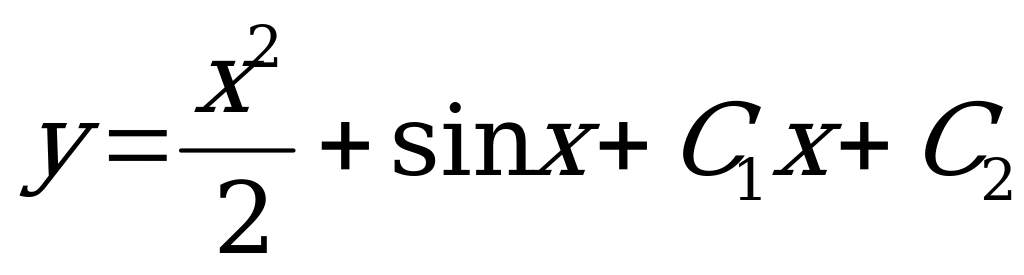2) 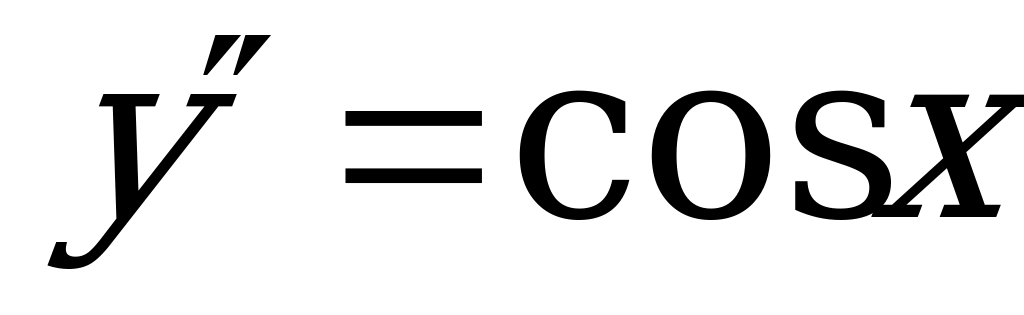(Ответ: )

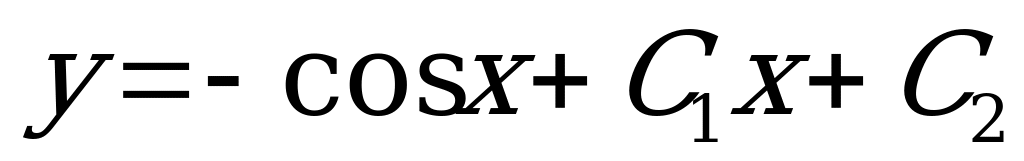4. Однородные линейные ДУ II порядка с постоянными коэффициентами:

1) 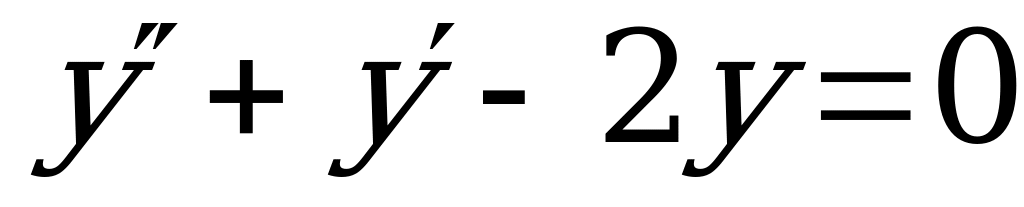(Ответ: )

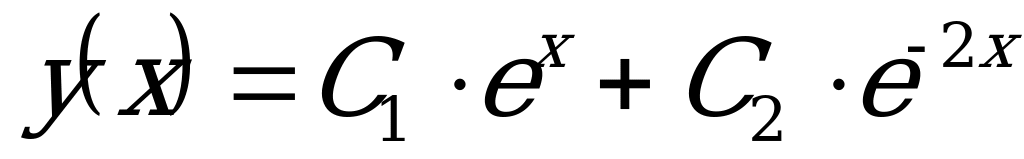2) 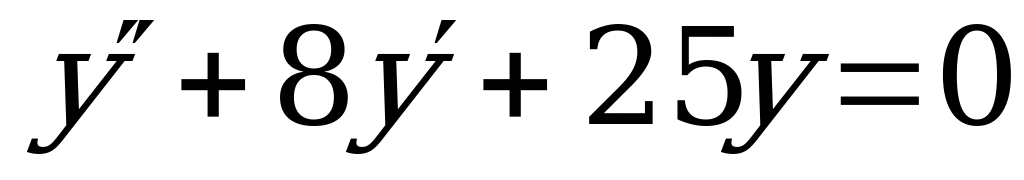(Ответ: )

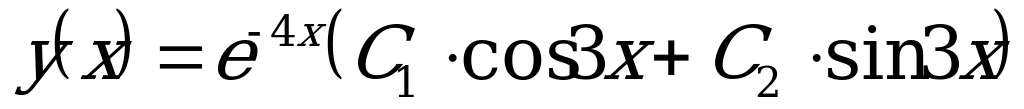Самостоятельная работа

Вариант №1

Решите уравнения:

1.

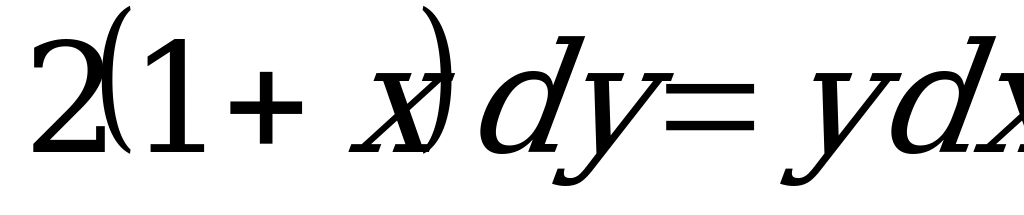
2.

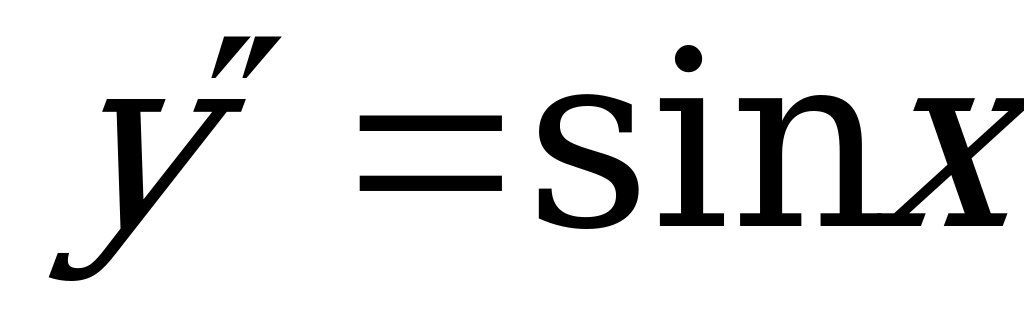
3. .

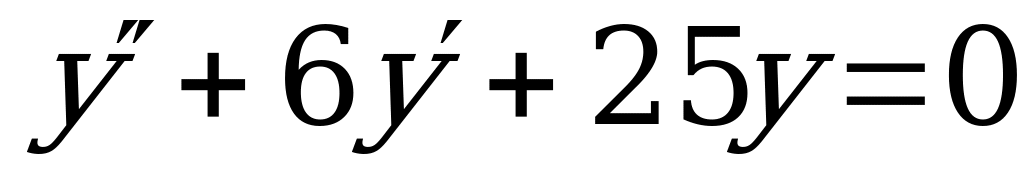Вариант №2

Решите уравнения:

1.

2.

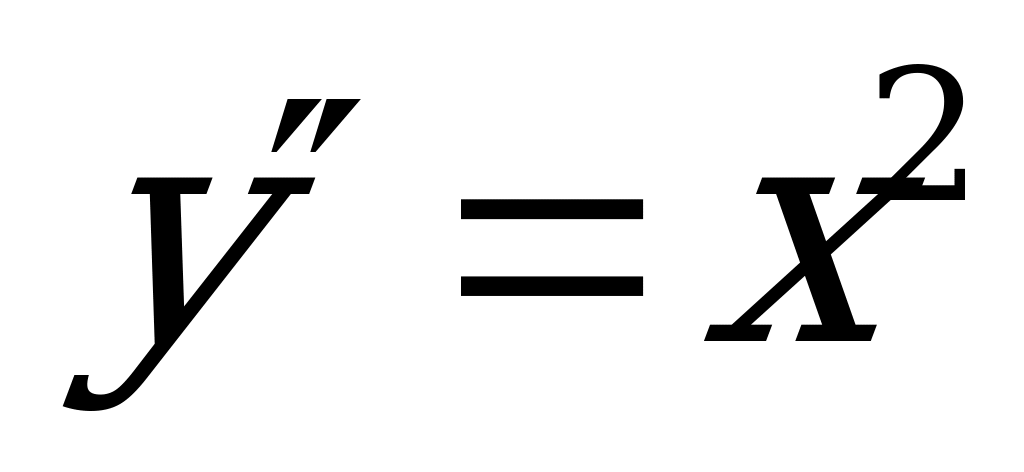
3. .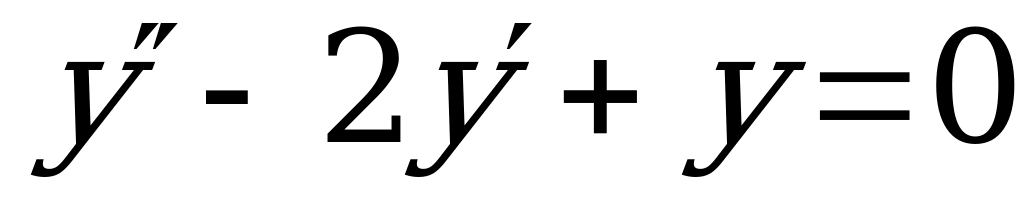
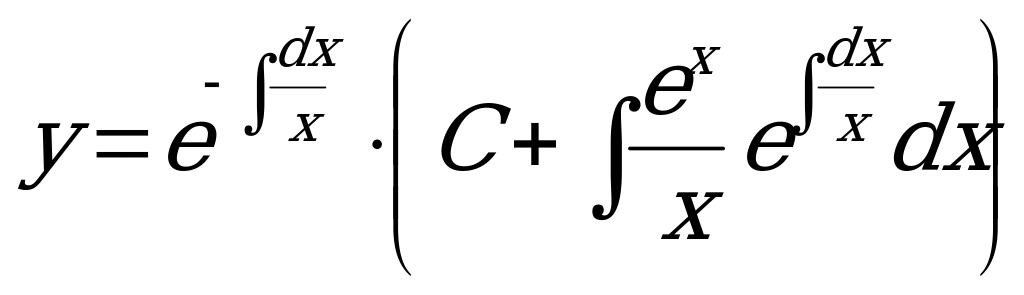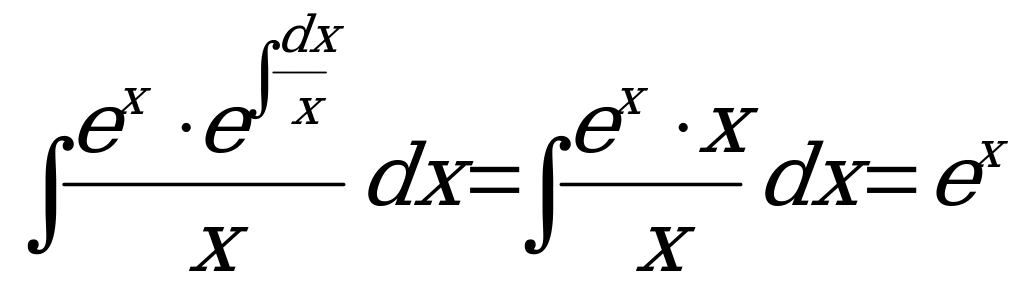