Решение неравенств с одной переменной

Основные понятия

• Решением неравенства с одной переменной называется…

такое значение переменной, при котором получается верное числовое неравенство.

• Два неравенства с одной переменной называют равносильными, если…

2X – 6 0

решения этих неравенств совпадают.

2x

Какие из трех неравенств являются равносильными?

2x 6

• Если оба неравенства не имеют решения, то это тоже равносильные неравенства .

y, то x – y 0 2. Если обе части неравенства с одной переменной умножить или разделить на одно и то же положительное число, то получится неравенство, равносильное данному: если x y, то a · x a · y, при a 0 3. Если обе части неравенства с одной переменной умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное данному: если x y, то –a · x 0 " width="640"

Свойства неравенств

• Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится неравенство, равносильное данному:

если x y, то x – y 0

2. Если обе части неравенства с одной переменной умножить или разделить на одно и то же положительное число, то получится неравенство, равносильное данному:

если x y, то a · x a · y, при a 0

3. Если обе части неравенства с одной переменной умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное данному:

если x y, то –a · x 0

Повторим алгоритм решения линейного неравенства

• Раскрой скобки
• Перенеси неизвестные слагаемые в левую часть неравенства, а известные – в правую; при этом не забудь поменять знак слагаемых на противоположный
• Приведи подобные в каждой части неравенства
• Раздели число в правой части на коэффициент при неизвестном; при этом не забудь: если делим на отрицательное число, знак неравенства меняем на противоположный.
• На числовом луче отметь полученное число, укажи интервал

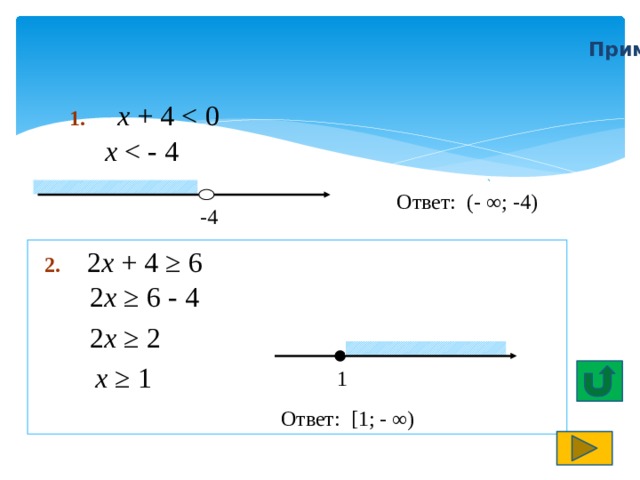
Примеры решения линейных неравенств

1. x + 4

x

Ответ: (- ∞; -4)

-4

2. 2 x + 4 ≥ 6

2 x ≥ 6 - 4

2 x ≥ 2

x ≥ 1

1

Ответ: [1; - ∞)

1) Решение

1) х + 2 ≥ 2,5 х -1

х – 2,5 х ≥ -1 - 2

– 1,5 х ≥ -3

: (-1,5)

х ≤ 2

x

2

Ответ: (- ∞; 2]

3 х - 0,25 х - 1 + 1,5 х – 0,5 3 х - 0,25 х + 1,5 х 3+1+0,5 2,25 х 4,5 х 2 x 2 Ответ: (2; +∞) " width="640"

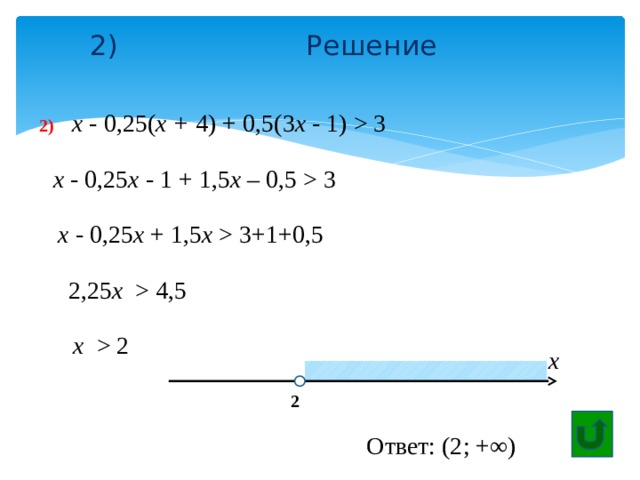
2) Решение

2) х - 0,25( х + 4) + 0,5(3 х - 1) 3

х - 0,25 х - 1 + 1,5 х – 0,5 3

х - 0,25 х + 1,5 х 3+1+0,5

2,25 х 4,5

х 2

x

2

Ответ: (2; +∞)

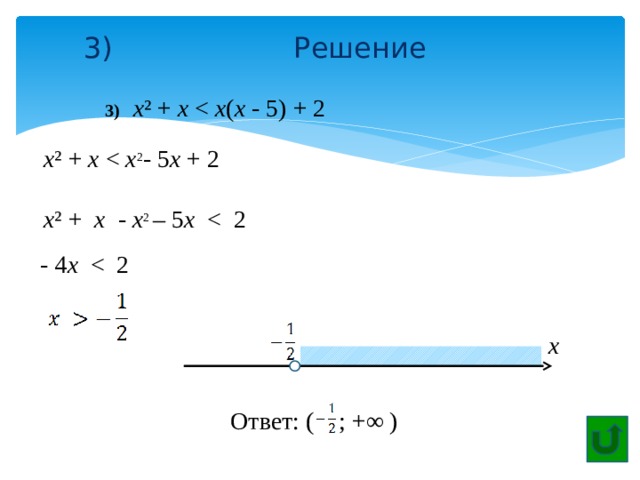
3) Решение

3) х ² + х х ( х - 5) + 2

х ² + х х 2 - 5 х + 2

х ² + х - х 2 – 5 х

- 4 х

x

Ответ: ( ; +∞ )

4) Решение

4 х – 16 – 9 х + 15 ≥ 24

: (-5)

x

-5

Ответ: (-∞ ; -5 ]

5) Решение

x

Ответ: (-∞; ]

115 2 . Какой из промежутков является решением неравенства -15x  45 А) -3 Б) -3 В) -3 3 Ответ: " width="640"

Устная работа

1. Назовите несколько чисел, которые являются решением неравенства 5x 115

2 . Какой из промежутков является решением неравенства -15x  45

А)

-3

Б)

-3

В)

-3 3

Ответ:

3? Ответ: " width="640"

Устная работа

3. Какой из промежутков является решением неравенства

4x + 19  5x – 1

А) ( -  ; 20  ; Б)  -20; 20  ; В) ( 20;  ); Г)  20;  )

Ответ:

4. Является ли решением системы неравенств числа

4; -1; 5,5

3x

2x +1 3?

Ответ:

14 ? Ответ: 6. Решите систему неравенств и выберите верный ответ: х – 4  12, 2x – 1 3, 3x +2 А) (-  ; 16  Б) ( 16; 18) В) (2; 18) Г)  16; 18) Ответ: " width="640"

Устная работа

5. Какое наибольшее целое число удовлетворяет неравенству -2x 14 ?

Ответ:

6. Решите систему неравенств и выберите верный ответ: х – 4  12,

2x – 1 3,

3x +2

А) (-  ; 16  Б) ( 16; 18) В) (2; 18) Г)  16; 18)

Ответ:

0 II. Найдите наименьшее целое число, являющееся решением неравенства 0,2(2 х +2) - 0,5( х -1) III. Найдите наименьшее натуральное число, являющиеся решением неравенства 3 х - 3 х + 4 " width="640"

Реши задачи

I. Найдите наибольшее целое число, являющееся решением неравенства

2( х -3) - 1-3( х -2) - 4( х +1) 0

II. Найдите наименьшее целое число, являющееся решением неравенства

0,2(2 х +2) - 0,5( х -1)

III. Найдите наименьшее натуральное число, являющиеся решением неравенства

3 х - 3 х + 4

0 2 х - 6 - 1- 3 х + 6 - 4 х - 4 0 -5 х - 5 0 х -5 х 5 х -1 -2 -3 x (-∞; -1) Ответ: -2 " width="640"

Реши задачу I.

I. Найдите наибольшее целое число, являющееся решением неравенства

2( х -3) - 1-3( х -2) - 4( х +1) 0

2 х - 6 - 1- 3 х + 6 - 4 х - 4 0

-5 х - 5 0

х

-5 х 5

х

-1

-2

-3

x (-∞; -1)

Ответ: -2

- 11 -11 -10 -9 x (-11; +∞) Ответ: - 10. " width="640"

Реши задачи II.

II. Найдите наименьшее целое число, являющееся решением неравенства

0,2(2 х +2) - 0,5( х -1)

0,4 х + 0,4 - 0,5 х +0,5

- 0,1 х + 0,9

- 0,1 х

- 0,1 х

x

х - 11

-11

-10

-9

x (-11; +∞)

Ответ: - 10.

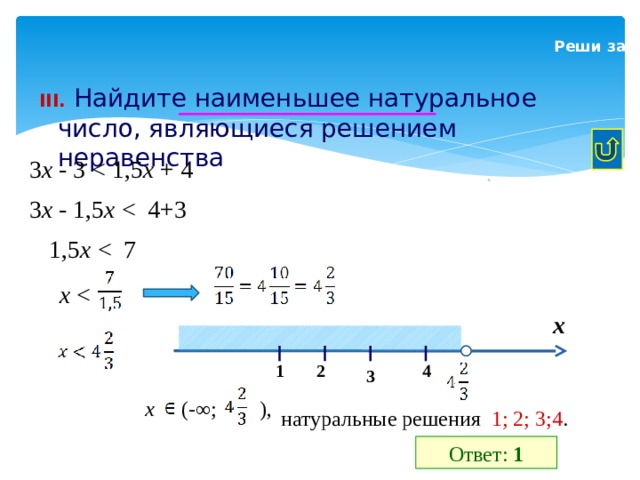
Реши задачи III.

III. Найдите наименьшее натуральное число, являющиеся решением неравенства

3 х - 3 х + 4

3 х - 1,5 х

1,5 х

х

х

2

1

4

3

x (-∞; ),

натуральные решения 1; 2; 3;4 .

Ответ: 1

Домашнее задание:

Решить задания с презентации: https://cloud.mail.ru/public/4NTZ/3QqKS4XMs