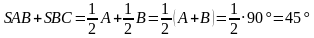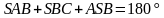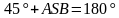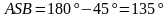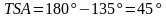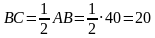Просмотр содержимого документа
«Решение задач по теме «Прямоугольные треугольники»»
Дата
Тема: Решение задач по теме «Прямоугольные треугольники»
Задачи: обобщить теоретические знания учащихся и закрепить навыки решения задач по теме.
Ход урока
АКТУАЛИЗАЦИЯ ЗНАНИЙ
Опрос по свойствам прямоугольного треугольника.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Открываем тетради и записываем сегодняшнее число и тему урока. Продолжаем подготавливаться к предстоящей контрольной работе. Выполняем письменно приведенные задания.
Задача 1.
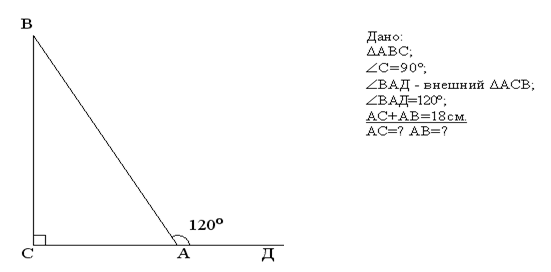
Решение: Найдем угол ВАС с помощью внешнего угла ВАD:
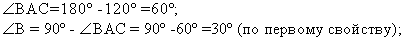
Катет, лежащий против угла в 30°, равен половине гипотенузы:
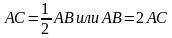
Пусть АС=х, тогда АВ=2х. Составим и решим уравнение:
х+2х=18,
3х=18,
х=АС=6,
АВ=2х=12.
Ответ: 6 см, 12 см.
Задача 2. Один острый угол прямоугольного треугольника на 60° больше другого. Найдите больший острый угол.
Дано: АВС – прямоугольный треугольник, угол С=90°, угол В больше угла А на 60°.
Найти: угол В.
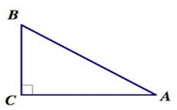
Решение. Пусть угол А=х, тогда угол В=х+60°. Применим свойство прямоугольного треугольника: сумма острых углов равна 90°. Тогда составим и решим уравнение:
х+х+60°=90°,
2х=90°-60°=30°,
х= 15°,
угол А=15°,
угол В=15°+60°=75°.
Ответ: 75°.
Задача 3. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника.
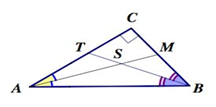
Дано: АВС – прямоугольный треугольник, угол С=90°, BT и AM – биссектрисы.
Найти: угол ASB или TSA.
Решение. Сумма острых углов прямоугольного треугольника равна 90°:
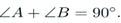
Угол 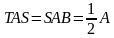 , угол
, угол 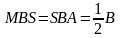 .
.
Найдем их сумму:
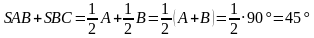
Применим теорему о сумме углов треугольника:
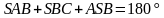
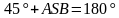
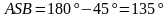
Но угол в 135° не является острым. Поэтому необходимо найти угол TSA, применяя теорему о смежных углах:
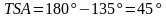
Ответ: 45°.
Задача 4. Лестница эскалатора метро длиной 40 м направлена под углом 30° к поверхности земли. На какой глубине находится метро.

Дано: АВ – лестница эскалатора, АВ=40 м, угол ВАС=30°.
Найти: ВС – глубина.
Решение. Действительно, данную задачу можно интерпретировать через прямоугольный треугольник. Представим, что лестница эскалатора – это гипотенуза прямоугольного треугольника. Известно, что она составляет с поверхностью земли угол в 30°. Тогда глубина метро, которая является катетом ВС, находится с помощью свойства катета против угла в 30°:
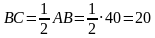
Ответ: 20 м.
ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ
Домашнее задание: повторить теорию по теме «Прямоугольные треугольники»









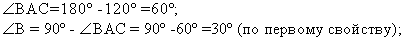
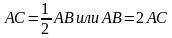


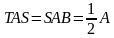 , угол
, угол 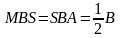 .
.