10 класс
Тема: «Теорема о трёх перпендикулярах»
Цель: Доказать теорему о трёх перпендикулярах, развивать логическое мышление, учить через моделирование, выдвигать гипотезы и доказывать их.
Тип урока: Урок усвоения новых знаний.
План.
1. Актуализация опорных знаний.
2. Мотивация урока.
3. Объяснение нового материала.
4. Решение задач.
5. Итог урока.
Ход урока.
I. Актуализация опорных знаний:
1. Что называется перпендикуляром к плоскости.
2. Что такое наклонная плоскости?
3. Проекция наклонной.
4. Свойства перпендикулярных прямых и плоскости.
5. Признак перпендикулярности прямых и плоскости.
6. Расстояние от точки до плоскости.
7. Расстояние от точки до прямой.
II. Мотивация урока.
Вот наклонная – красавица
Надеюсь вам она понравится
(А здесь проекции её)
Друг без друга ни куда,
Дружат – не разлей вода.
Для обычной для прямой
Мы дадим задание:
Стать для первой и второй
Перпендикулярной…
Думайте и не спешите
Как возможно это?
Где прямая стать должна?
Жду от вас ответа.
(Учащиеся моделируют с помощью стереометрических ящиков)
Объявляется тема и цель урока.
III. Объяснение нового материала.
Теорема: (ТТП). Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна наклонной.
Дано:
 : АВ
: АВ 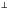
 .
.
АС – Наклонная
С,
т С  с
с
ВС 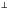 c
c
Доказать:
АС 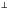 с.
с.

Попробуйте сформулировать теорему, обратную ТТП.
Теорема. (обратная) Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и её проекции.
Устно. Установите взаимное расположение прямых a и b по рисунку.
 ABCD – квадрат
ABCD – квадрат
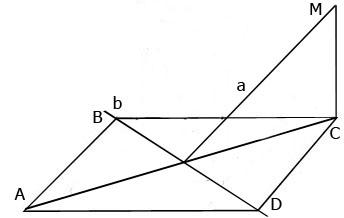 ABCD – ромб
ABCD – ромб
Алгоритм нахождения расстояния от точки, не лежащей в плоскости, до прямой, содержащейся в плоскости.
1. Найти перпендикуляр, проведённый из данной точки на плоскости.
2. Указать наклонную и её проекцию.
3. Доказать, что прямая перпендикулярна проекции наклонной и ссылаясь на ТТП, утверждать, что прямая перпендикулярна наклонной.
4. Наклонная перпендикулярна прямой, значит, длина наклонной и есть расстоянием от точки до прямой.
Решение задач:
Задача: В  ABC ,
ABC ,  A = 30
A = 30 ;
;  B = 60
B = 60
AD 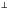 (ABC). Доказать CD
(ABC). Доказать CD 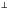 BC.
BC.
Дано: Доказательство:
 ABC
ABC  ABC:
ABC:
 A = 30
A = 30
 С = 180
С = 180 - (30
- (30 + 60
+ 60 )
)
 B = 60
B = 60 = 90
= 90
AD 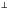 (ABC) АС
(ABC) АС 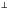 ВС
ВС
Доказать: AD –перпендикуляр
CD 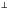 BC DC – наклонная
BC DC – наклонная
АС – проекция
АС 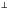 СВ, по ТТП DС
СВ, по ТТП DС 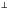 СВ
СВ

Итог: п.148, доказательство обратной теоремы
Из истории: Аналитический способ доказательства предложил Рене Декарт.
В первой книге по геометрии «Начала» Евклида нет доказательства ТТП.







 : АВ
: АВ 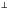
 с
с 
 ABCD – квадрат
ABCD – квадрат ABCD – ромб
ABCD – ромб ABC ,
ABC ,  A = 30
A = 30 ;
; 









