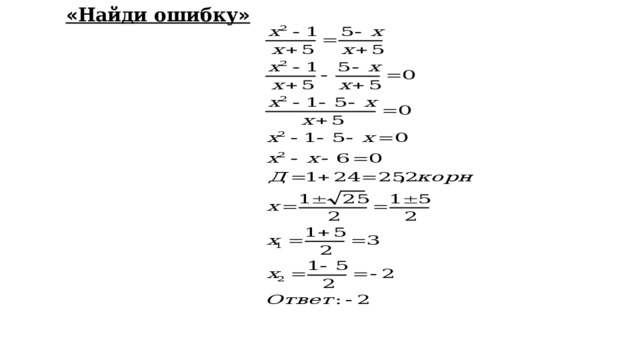Уравнения, виды уравнений и способы их решений

Девиз урока « Считай несчастным тот день или тот час, в котором, ты не усвоил ничего, ничего не прибавил к своему образованию» . Ян Амос Каменский

Жить – значит иметь проблемы.

Решать их – значит расти интеллектуально.

Дж.Гилфорд, психолог

Установка на успех

1 .Определи для себя значение данного материала. 2 .Наметь цель и не отступай от неё. 3. Радуйся, когда тебе удастся достичь хотя бы маленького успеха. 4. Не огорчайся, если с первого раза не удастся. Попробуй ещё раз. 5. Не бойся попросить помощи. 6. Спрашивай, если в чём-то сомневаешься. 7. Я верю, что каждый из вас справится.

Успехов, вам !

Проверь себя

Пример 3 .

Пример 1 .

Пример 2.

Общий знаменатель х(1-х)

Общий знаменатель 2(x+1)(х -1) =2( х 2 -1)

Общий знаменатель (x+6)(х -1)(х+3)

Ответ: -8.

x = -8

нет решений

Ответ: нет решений .

x 1 =6, x 2 = - 2,2.

Ответ: -2,2; 6 .

Решите устно

Создатель теории относительности Альберт Эйнштейн в своё время заметил: «Мне приходится делить свое время между политикой и уравнениями . Однако уравнения для меня важнее, потому что политика — для настоящего , а уравнения — для вечности»

АЛЬБЕРТ ЭЙНШТЕЙН

14.03.1879 -18.04.1955

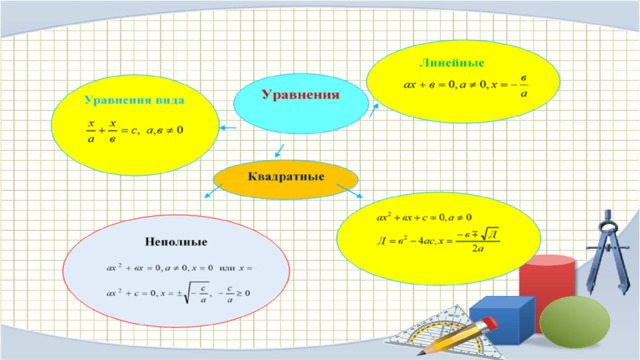
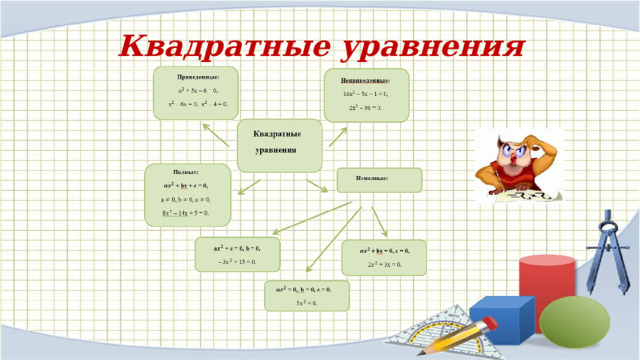
Квадратные уравнения

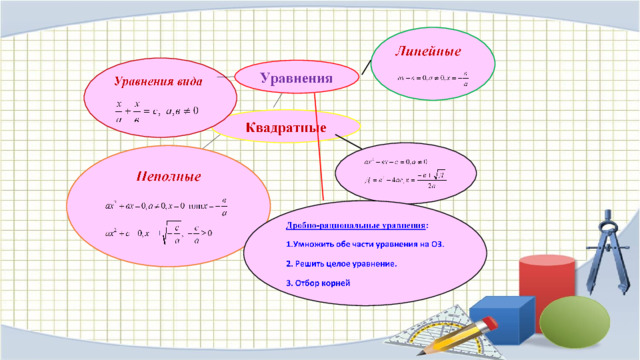
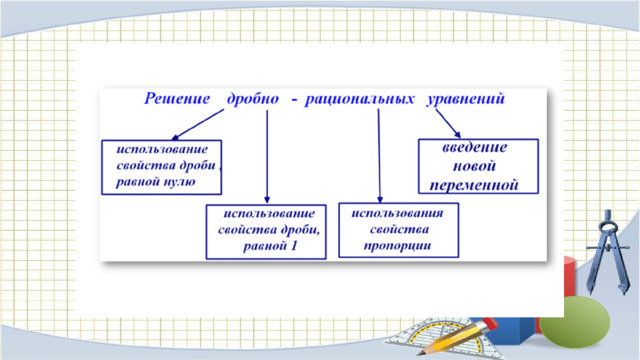
Способы решения дробных рациональных уравнений

1. Приведение дробей к общему знаменателю.

2.Умножение дробей на общий знаменатель всех дробей.

3.Графический.

4.Введение новой переменной.

5.Выделение из дроби целой части.

Решим уравнение

Решение. ОДЗ: х≠2

Умножим обе части уравнения на (х-2), получим

2х²-(3х+2)=х(х-2),

2х²-3х-2=х²-2х,

2х²-3х-2-х²+2х=0,

х²-х-2=0,

D=1+8=9,

х=(1±3):2,

х₁=-1, х₂=2.

Если х=-1, х-2=-1-2=-3≠0;

если х=2, то х-2=2-2=0.

Решить уравнение

∙ 6

Наименьший общий знаменатель

Решим целое уравнение

Решим дробное рациональное уравнение

∙ 6

0

0

Если x= 5, то

Если x= - 2, то

Ответ: 1,5

Ответ: - 2

Целое рациональное уравнение

Дробные рациональные уравнения

Левая и правая части каждого равенства являются рациональными выражениями. Такие уравнения называются рациональными уравнениями .

Алгоритм решения дробно-рационального уравнения:

1) найти общий знаменатель дробей, входящих в уравнение;

2) умножить обе части уравнения на общий знаменатель;

0

0

3) решить получившееся целое уравнение;

Если x= 5, то

4) исключить из его корней те, которые обращают в нуль общий знаменатель.

Если x= - 2, то

Ответ: - 2

Пример.

Алгоритм решения дробно-рационального уравнения:

1) найти общий знаменатель дробей, входящих в уравнение;

2) умножить обе части уравнения на общий знаменатель;

3) решить получившееся целое уравнение;

4) исключить из его корней те, которые обращают в нуль общий знаменатель .

Ответ: 3

Решим дробное рациональное уравнение

Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называют дробным.

Вопрос:

Какие рациональные уравнения называются дробными?

Решим уравнение

Решим уравнение

ОДЗ: х≠0; х≠-1;х≠-2

Общий знаменатель: 4х(х+1)(х+2). Умножим обе части уравнения на 4х(х+1)(х+2), получим

4(х+2)+ 4х=х(х+1)(х+2),

4х+8+4х=х(х²+3х+2),

8х+8=х³+3х²+2х,

х³+3х²-6х-8=0,

(х³-8)+3х(х-2)=0,

Решим уравнение:

Решение.

ОДЗ: х ≠ -2, х ≠ 3

(х+2)(х-3) – общий знаменатель.

Умножим обе части уравнения на (х+2)(х-3), получим (х-1)(х-3)=(х-4)(х+2)- (х+2)(х-3),

х²-х-3х+3=х²-4х+2х-8-х²-2х+3х+6,

х²-3х+5=0,

D=9-20

Ответ: корней нет

Решим уравнение:

х-1 – общий знаменатель.

Умножим обе части уравнения на х-1,

получим 2(х-1)-(х+1)=0;

2х-2-х-1=0,

х-3=0,

х=3.

Если х=3, то х-1=3-1=2 ≠0.

Ответ:3

метод «Шести шляп» мышление делится на шесть различных режимов , каждый из которых представлен шляпой своего цвета.

Белая шляпа (факты)

Собираем информацию, которая у нас имеется.

А имеются …... Необходимо определить …….

Как это сделать?

Чёрная шляпа (критика)

Какие имеются недостатки, проблемы в решении задачи

Красная шляпа (чувства)

есть ли у вас предложения, как решить задачу, что необходимо сделать?

Жёлтая шляпа (оптимизм)

Каким правилом можно воспользоваться, чтобы узнать ….?

Зелёная шляпа (креативность)

Мы определили, что…

Синяя шляпа (процесс)

решим полученное уравнение …

3.71. Тракторист должен был вспахать за некоторое время поле площадью 180 га. Но ежедневно он вспахивал на 2 га больше, чем планировал, поэтому закончил работу на 1 день раньше срока. За сколько дней тракторист вспахал поле?

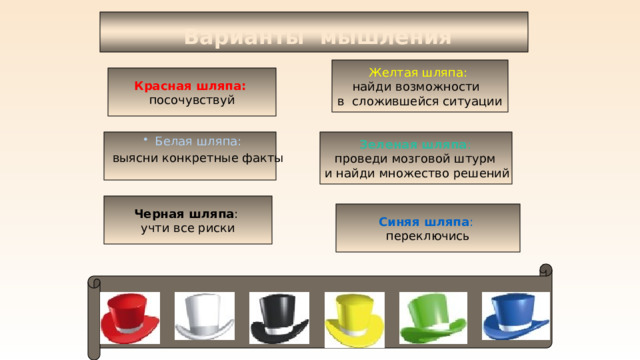
Варианты мышления

Желтая шляпа:

найди возможности

в сложившейся ситуации

Красная шляпа:

посочувствуй

• Белая шляпа:

Зеленая шляпа :

проведи мозговой штурм

выясни конкретные факты

и найди множество решений

Черная шляпа :

учти все риски

Синяя шляпа :

переключись

Синяя шляпа

Организация мышления. Мышление о мышлении. Чего мы достигли? Что нужно сделать дальше?

Зелёная шляпа

Творчество. Различные идеи. Новые идеи. Предложения. Каковы некоторые из возможных решений и действий? Каковы альтернативы?

Жёлтая шляпа

Преимущества. Почему это стоит сделать? Каковы преимущества? Почему это можно сделать? Почему это сработает?

Чёрная шляпа

Осторожность. Суждение. Оценка. Правда ли это? Сработает ли это?

В чем недостатки?

Что здесь неправильно?

Белая шляпа

Информация. Вопросы. Какой мы обладаем информацией? Какая нам нужна информация?

Красная шляпа

Эмоции. Интуиция, чувства и предчувствия. Не требуется давать обоснование чувствам. Какие у меня по этому поводу возникают чувства?

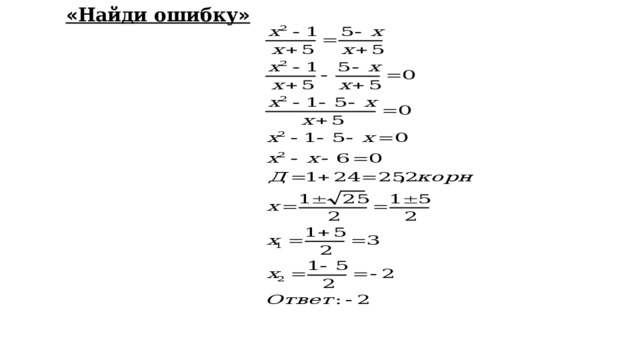
« Найди ошибку »

Физкультминутка