Просмотр содержимого документа
«Урок геометрии Параллелограмм и трапеция»
ПАРАЛЛЕЛОГРАММ И ТРАПЕЦИЯ
Цели: доказать признаки параллелограмма и рассмотреть решение задач.
Ход урока
I. Проверка домашнего задания.
1. Ответить на вопросы учащихся по домашнему заданию.
2. Выполнить задания (устно):
1) На рисунке а) 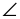 1 =
1 = 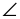 4,
4, 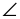 2 =
2 = 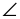 3. является ли четырехугольник АВСD параллелограммом?
3. является ли четырехугольник АВСD параллелограммом?
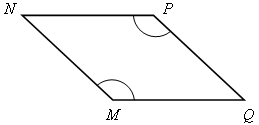
2) На рисунке б) 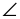 1 =
1 = 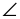 2 =
2 = 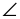 3. Докажите, что четырехугольник АВСD – параллелограмм.
3. Докажите, что четырехугольник АВСD – параллелограмм.
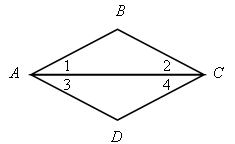
3) На рисунке в) ММ || РQ, 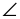 М =
М = 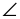 Р. Докажите, что МNPO – параллелограмм.
Р. Докажите, что МNPO – параллелограмм.
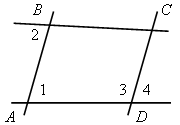
4) Является ли четырехугольник АВСD, изображенный на рисунке г), параллелограммом, если а) 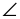 1 = 70°;
1 = 70°; 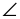 3 = 110°;
3 = 110°; 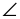 2 +
2 + 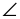 3 = 180°;
3 = 180°;
б) 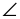 1 =
1 = 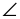 2,
2, 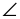 2 ≠
2 ≠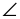 4?
4?

а) б)
в) г)
3. Анализ самостоятельной работы.
II. Изучение нового материала.
1. Перед тем как приступить к изучению признаков параллелограмма, следует напомнить учащимся, что означает слово «признак» и что такое обратная теорема.
2. Предложить учащимся самим сформулировать теоремы, обратные утверждениям о свойствах параллелограмма.
3. Подчеркнуть, что некоторое утверждение верно, но отсюда еще не следует, что верно и обратное ему утверждение.
4. Доказательство признаков можно провести силами учащихся.
III. Закрепление изученного материала.
Решить задачи №№ 379, 382.
№ 379.
Решение
3) Тогда ВK = DМ.
4) Четырехугольник ВМDK является параллелограммом, так как
ВK || DМ, ВK = DМ.
№ 382.
Решение
| | 1) По свойству параллелограмма АО = ОС, ВО = ОD. 2) По условию ВВ1 = В1О = ОD1 =
= D1D и АА1 = А1О = ОС1 = С1С. 3) Четырехугольник А1В1С1D1 – параллелограмм, так как его диагонали пересекаются и точкой пересечения делятся пополам. |
IV. Итоги урока.
Если в задаче необходимо доказать, что АВСD – параллелограмм, то применяют один из признаков:
| АВ || СD и ВС || СD | 
| АВСD – параллелограмм |
| АВ || СD и АВ = СD | 
| АВСD – параллелограмм |
| АВ = СD и АD = ВС | 
| АВСD – параллелограмм |
| АО = ОС и ВО = ОD | 
| АВСD – параллелограмм |
Домашнее задание: вопросы 6–9, с. 114; №№ 380, 373, 377, 384.






















