Задача о лебеде, раке и щуке

История о том, как «лебедь, рак да щука везти с поклажей воз взялись» – известна, конечно, всем. Но пробовали ли вы проверять этот рассказ на основании законов механики? Результат проверки получается, сверх ожидания, вовсе не похожий на вывод баснописца.

Будем рассуждать так, словно перед нами обыкновенная задача на сложение нескольких сил, действующих под углом одна к другой. Направление сил определено в басне:

…Лебедь рвется в облака,

Рак пятится назад, а щука тянет в воду.

Это значит, что одна сила, тяга лебедя (А), направлена вверх; другая, тяга щуки (В) – вбок; третья, тяга рака (С) – назад. Не забудем, что существует еще четвертая сила, вес воза, которая направлена отвесно вниз. Крылов утверждает, что «воз и ныне там», – другими словами, что равнодействующая всех четырех сил в данном случае равна нулю.

Так ли это?

Посмотрим. Лебедь, рвущийся к облакам, не только не мешает работе рака и щуки, но даже помогает им: тяга лебедя, направленная против силы тяжести, облегчает вес воза, а может быть, даже и вполне уравновешивает его – ведь груз невелик («поклажа бы для них казалась и легка»). Остаются всего две силы: тяга рака и тяга щуки. О направлении этих сил говорится, что «рак пятится назад, а щука тянет в воду». Само собою разумеется, что вода находилась не впереди воза, а сбоку (не потопить же воз собрались крыловские труженики!). Но если силы рака и щуки направлены под углом одна к другой, то равнодействующая их никак не может равняться нулю.

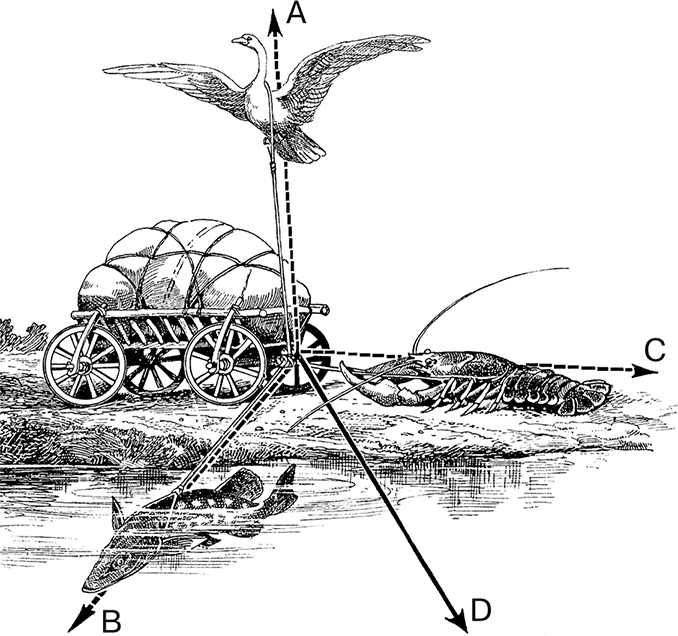
Задача о лебеде, раке и щуке, решенная по правилам механики. – Равнодействующая D должна сдвинуть воз с места.

Поступая по правилам механики, строим на обеих силах В и С параллелограмм; диагональ его D дает направление и величину искомой равнодействующей. Ясно, что эта равнодействующая сила должна сдвинуть воз с места, тем более что вес воза вполне или частью уничтожается тягою лебедя (трением мы здесь, ради простоты, пренебрегаем). Другой вопрос – в какую сторону сдвинется воз: вперед, назад или в бок; это зависит от соотношения сил и от величины угла между ними.

Во всяком случае, как видите, Крылов едва ли мог с уверенностью утверждать, что «возу все нет ходу», что «воз и ныне там».