Россия, Вязьма
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 26.11.2024 11:44
камышкова жанна валентиновна
учитель математики
57 лет
15 406
2 368 
Местоположение
Специализация
Задачи для проведения олимпиад по математике в 10-11 классах
Категория:
Математика
04.09.2017 18:57
Просмотр содержимого документа
«Задачи для проведения олимпиад по математике в 10-11 классах»
Задачи к олимпиаде по математике 10 – 11 класс.
№ 1. Укажите сумму всех целых чисел К, при которых выражение
(6К2-13К-5):(3К+4) является целым числом.
а) -10; б) 1; в) 10; г) 23.
№ 2. При каких значениях параметра а уравнение |х-2|+|х-3|=а не имеет решений?
а) а≤1; в) а≤0; г) а
№ 3. Укажите количество целых значений параметра а, при которых абсцисса и ордината вершины параболы у=(х-2а)2-а2-8а-15 положительны.
а) 0; б) 1; в) 2; г) 3.
№ 4. Найдите число целых решений неравенства │2х-5│+│4-х│≤х+1.
а) 4; б) 3; в) 2; г) 1.
№ 5. Найдите сумму всех чётных чисел К, каждое из которых делится без остатка на 33 и удовлетворяет условию -396≤К
а) -726; б) -792; в) 530; г) -131.
№ 6. Если в окружности хорда длиной 30 см перпендикулярна диаметру и делит его в отношении 1:9, то диаметр окружности равен
а) 50 см; б) 45 см; в) 40 см; г) 35 см.
№ 7. Найдите сумму корней уравнения │(х-4)3-36│=28.
а) 14; б) -10; в) 8; г)0.
№ 8. Найдите площадь четырёхугольника, ограниченного прямыми
2у-3х=12, 2у-3х=18 и осями координат .
а) 15; б) 6; в) 1,5; г) 30.
№ 9. Если точка касания вписанной в прямоугольный треугольник окружности делит катет на отрезки 5 см и 7 см, то периметр треугольника равен:
а) 84 см; б) 44; в) 104; г) 94.
№ 10. Найдите сумму корней уравнения │х+1│=2│х-2│.
а) 6; б) 3; в) 0; г) корней нет.
№ 11. Около равнобедренного треугольника АВС с основанием АС и углом при основании 75ᵒ описана окружность с центром О. Найдите её радиус, если площадь треугольника ВОС равна 16.
а) 8; б) 4; в) 2; г) 5.
№ 12. Найдите значение функции у=(3f(x)-2f(-x)):(2g(x)-3g(-x)) в точке х0, если известно, что функция у=f(x ) четная, функция y=g(x) нечётная, f(x0)=5, g(x0)=1.
а) 1; б) -5; в) 25; г) -1.
№ 13. Первоначальная цена товара на торгах повышалась несколько раз на одно и то же количество рублей. После третьего повышения цена равнялась 1200 рублей, а после двенадцатого повышения – 1650 рублей. Через сколько повышений первоначальная цена удвоилась?
а) 21; б) 50; в) 42; г) 10.
№ 14. Имеются два слитка сплава серебра и олова. Первый слиток содержит 360 г серебра и 40 г олова, а второй слиток – 450 г серебра и 150 г олова. От каждого слитка взяли по куску, сплавили их и получили 200 г сплава, в котором оказался 81% серебра. Определите массу (в граммах) куска, взятого от второго слитка.
а) 120; б) 80; в) 100; г) 162.
№ 15. За 10 дней Карл украл у Клары 165 кораллов и из них 147 в первые 7 дней. Каждый день он крал на одно и то же число кораллов меньше, чем в предыдущий день. Сколько кораллов Карл украл в десятый день?
а) 3; б) 4; в) 1; г) 2.
№ 16. Сколько граммов воды нужно выпарить из 0,5 кг солевого раствора, содержащего 85% воды, чтобы получить массу с содержанием 75% воды.
а) 200; б) 100; в) 125; г) 150.
№ 17. Площадь треугольника АВС равна 15. На стороне АС взята точка D так, что AD:DC=2:3. Длина перпендикуляра DН, проведённого на сторону ВС, равна 6. Найдите ВС.
а) 3; б) 10/3; в) 5; г) 7,5.
№ 18. В равнобедренном треугольнике высоты, проведённые к основанию и боковой стороне, равны соответственно 5 и 6. Найдите длину боковой стороны.
а) 6,25; б) 6,5; в) 6; г) 5,6.
№ 19. Число 200 увеличили на 30%, полученное число увеличили на 20%. Какое число получится в итоге?
а) 312; б) 300; в) 250; г) 350.
№ 20. Сколько процентов числа 7 составляет разность между ним и 4% числа 28?
а) 84%; б) 50%; в) 1,12%; г) 5,88%.
№ 21. При каких значениях а парабола у=9х2 -12х+20а касается оси абсцисс?
а) а=0,2; б) а0; в) а
№ 22. Решите уравнение (х2+2х)2-(х+1)2=55
а) -4; 2; б) -7; 8; в) корней нет; г) 5; 11.
№ 23. Количество целых значений параметра а, при которых абсцисса вершины параболы у=(х-6а)2+а2-5а-6 положительна, а ордината отрицательна, равно:
а) 5; б) 6; в) 7; г) 0.
№ 24. Произведение корней уравнения (х-0,3)(х2-4)=(3х-0,9)(х+2)2
а) 2,4; б) 4,8; в) -2,4; г) -4,8.
№ 25. Решите неравенство I2х-1I5.
а) х3; б) х3; в) -2
№ 26. В многоугольнике с периметром 31 см провели диагональ d, которая разбила его на два многоугольника с периметрами 21 см т 30 см. Чему равна диагональ d?
а) 10; б) 10,5; в) 20; г) 15.
№ 27. В двух канистрах находится 90 л бензина. Если из первой канистры перелить во вторую 10% бензина, находящегося в первой канистре ,то в обеих канистрах бензина будет поровну. Сколько литров бензина в каждой канистре?
а) 50 л и 40 л; б) 45 л и 45 л; в)55 л и 35 л ; г) 52 л и 37 л.
№ 28. В кубе АВСDА1В1С1D1 найдите угол между прямыми АВ1 иВС1.
а) 60ᵒ; б) 90ᵒ; в) 45ᵒ; г) 30ᵒ.
№ 29. Насос может выкачать из бассейна 1/3 воды за 10 мин. Проработав 0,25 ч, насос остановился. Найдите вместимость бассейна, если после остановки насоса в бассейне осталось 40 м3 воды.
а) 80 м3; б) 120 м3; в) 100 м3; г) 90 м3.
№ 30. Вкладчик сначала снял со своего счёта в банке 1/5 своих денег, потом 5/16 оставшихся и ещё 999 рублей. После этого у него осталось на сберкнижке 1/4 всех денег. Каким был первоначальный вклад?
а) 3330; б) 4000; в) 3500; г) 3335.
№ 31. На выпускном экзамене по математике 1440 школьников решили задачи с ошибками,3120 школьников, сдававших экзамен в этот день, не решили ни одной задачи, а число школьников, решивших все задачи правильно, относится к числу не решивших ни одной задачи, как 5:3. Сколько школьников экзаменовалось по математике в этот день.
а) 9760; б) 6640; в) 5200; г) 12 630.
№ 32. В треугольник АВС вписана окружность радиуса 5, касающаяся стороны АС в точке D, стороны АВ в точке Е, стороны ВС в точке F. Отрезок АD равен радиусу окружности, СD=15. Найдите площадь треугольника ВЕF.
а) 40; б) 75; в) 150; г) 50.
№ 33. Найдите значение выражения (81/2·271/2·641/4)2/3-((1281/3)3/5)5/7.
а) 10; б) 0; в) -64; г) 100.
№ 34. Заработные платы рабочего за январь и февраль относятся как 9:8, а за февраль и март как 6:8. За март он получил на 450 рублей больше, чем за январь, и за перевыполнение квартального плана рабочему начислили премию в размере 20% его трёхмесячного заработка. Найдите размер премии.
а) 1494; б) 1035; в) 2250; г) 2070.
№ 35. Если длины сторон трапеции — целые числа, то ее периметр не может быть равен
а) 6; б) 5; в) 7; г) 2013.
№ 36. Две окружности имеют общий центр. Хорда большей окружности имеет длину 20 и касается меньшей окружности. Чему равна площадь закрашенного кольца?
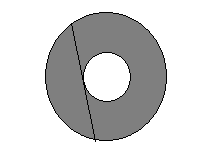
а) 100π; б) 150π; в) 200π; г) 250π.
№ 37. Чему равна сумма х+у, если х2-6х=2ху-х2-у2-9?
а) 6; б) 0; в) 3; г) невозможно определить .
№ 38. Биссектриса BL угла B в треугольнике ABC делит сторону AC в отношении 1 : 2 ( AL : LC = 1: 2 ). Какой угол образует эта биссектриса с медианой, проведенной из вершины A?
а) 90ᵒ; б) 45ᵒ; в) 60ᵒ; г) 30ᵒ.
№ 39. Сколько цифр содержит запись наименьшего натурального числа, которое делится на 225 и записывается (в десятичной системе) только нулями и единицами?
а) 11; б) 12; в) 10; г) 13.
№ 40. На какое число частей нельзя разделить плоскость четырьмя различными
прямыми?
а) 7; б) 8; в) 9; г) 10.
№ 41. Любитель арифметики перемножил первые 2013 простых числа. На сколько нулей оканчивается произведение?
а) 1; б) 0; в) 10; г) 100.
№ 42. Альберт всегда лжет. Однажды он сказал своему другу Франку: «Хотя бы один из нас никогда не лжет». Тогда обязательно
а) бывает, что Франк лжет; б) Франк всегда лжет;
в) Франк никогда не лжет; г) бывает, что Франк говорит правду.
№ 43. Мистеру Бину нужно 50 секунд, чтобы спуститься пешком по неподвижному эскалатору. Движущийся эскалатор поднимает его, стоящего на ступеньке, за 60 секунд. Сколько секунд нужно мистеру Бину, чтобы спуститься пешком по поднимающемуся эскалатору?
а) 300; б) 10; в) 300/11; г) 450.
№ 44. Вилли написал на листе два числа. В качестве третьего числа он написал сумму первого и второго, в качестве четвертого – сумму второго и третьего и т. д., пока не написал шестое число. Потом он сложил все шесть полученных чисел и заметил, что если знать такую сумму, то всегда можно точно определить, каким было одно из шести слагаемых. Какое?
а) пятое; б) шестое; в) второе; г) третье.
№ 45. Правильный шестиугольник и правильный треугольник имеют одинаковые периметры. Каково отношение их площадей?
а) 1,5; б) 2; в) 4; г) 6.
№ 46. Если сумма углов треугольника равна а, то квадрат угла квадрата равен
а) а2:4; б) а2:2; в) а:2; г) а:4.
№ 47. Маша старше Миши ровно на один месяц (дни их рождения приходятся на одно и то же число в двух соседних месяцах), а Даша старше Миши на столько же дней, на сколько Маша старше Даши. В каком месяце не могла родиться Даша?
а) в августе; б) в апреле; в) в мае; г) в декабре.
№ 48. Виноград содержит 90% влаги, а изюм – 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма?
а) 190; б) 100; в) 150; г) 120.
№ 49. У скольких двузначных чисел сумма цифр суммы цифр равна 1?
а) 10; б) 1; в) 2; г) 9.
№ 50. В корзине лежат 30 грибов - несколько белых и несколько подберезовиков. Если мы вынем 12 грибов, то среди них обязательно будет хотя бы один белый. Если мы вынем 20 грибов, то среди них обязательно
будет хотя бы один подберезовик. Сколько белых грибов в корзине?
а) 19; б) 11; в) 12; г) 29.
№ 51. Часовая стрелка часов имеет длину 4 см, а минутная – 8 см. Каково отношение расстояний, проходимых концами стрелок от 2 до 5 часов дня?
а) 1:24; б) 1:2; в) 1:12; г) 1:4.
№ 52. Если a и b — числа разных знаков, то самым большим из четырех чисел q=a2– b2, r = (a + b)2, s = (a – b)2, t = a2 + b2 является
а) s; б) q; в) r; г) t.
№ 53. По листу клетчатой бумаги со стороной клетки 1 см ползет жук. Он
проделал путь длиной 3 см. Каково наибольшее количество клеток,
внутри которых мог побывать жук?
а) 10; б) 3; в) 9; г) 11.
№ 54. Найдите все значения числового параметра а, при которых корни уравнения 
положительны.
а) аϵ[-1;-3/4]; б) аϵ(-1;-3/4]; в) аϵ[-1;-3]; г) аϵ[-1;0)
№ 55. Решите уравнение (х-2)(х-3)(х+4)(х+5)=1320. В ответе укажите сумму его корней.
а) -2; б) 2; в) 11; г) 0.
№ 56. Вычислить сумму a2006 + 1/a2006, если a2– а+ 1 = 0.
а) -1; б) 1; в) 2; г) 1,5.
№57. Дрожжевые грибки при благоприятных условиях размножаются с большой скоростью, увеличиваясь в объеме в 2 раза за каждую минуту. В колбу поместили 1 гриб, который заполнил ее за 30 минут. За сколько минут заполнят колбу помещенные в нее два гриба?
а) 29; б) 15; в) 14; г) 20.
№ 58. Программист дал объявление о поиске высокооплачиваемой работы.
Известно, что число предложений ему изменяется каждый день на одно и то
же число после его сообщения о поиске работы. На пятый день программисту поступило 26 предложений, а на двадцать пятый 6 предложений. Сколько всего предложений поступило программисту?
а) 465; б) 350; в) 395; г) 425.
№ 59. В процессе технологических операций из кожуха химического реактора в бассейн сначала откачали 50% имевшейся в нем воды, затем еще 100 л и, наконец, еще 5% остатка. В результате количество воды в бассейне
возросло на 31%. Сколько воды было в кожухе реактора первоначально, если
в бассейне вначале было 2000 л воды?
а) 1000; б) 1500; в) 300; г) 900.
№ 60. В треугольнике АВС АВ=10, угол А – тупой. Найдите медиану ВМ, если АС=20,а площадь треугольника АВС равна 96.
а) 16; б) 15; в) 12; г) 14.
№ 61. Найдите все значения параметра к, при которых прямая у=кх+2 имеет не менее трёх различных общих точек с графиком функции у=II3x-2I-4I.
а) [-1;3]; б) [3;12]; в) (-12;-3); г) (-12;-10).
№ 62. Покрасив два метра забора, Том Сойер «уступил» это занятие другому мальчику, который покрасил 30% неокрашенной части забора. После этого Том ещё трижды «уступал» своё право красить забор другим мальчикам. Первый и второй из них покрасили соответственно 1/5 и 1/6 всего забора, а третий – 85% оставшейся неокрашенной части. Найдите длину забора, если последний оставшейся метр Том красил сам.
а) 24,2; б) 24; в) 28,8; г) 32,4.
№ 63. Ученику прислали задание, состоящее из 20 задач. За каждую верно решённую задачу ему ставят 8 баллов, за каждую неверно решённую – минус 5 баллов, за задачу которую он не брался решать – 0 баллов. Ученик получил в сумме 13 баллов. Сколько задач он брался решать?
а) 13; б) 15; в) 10; г) 17.
№ 64. В классе находится учитель и несколько его лучших учеников. Найдите сколько учеников находится в классе, если возраст учителя больше их среднего возраста на 24 года и больше среднего возраста всех присутствующих в классе на 20 лет.
а) 5; б) 10; в) 15; г) 8.
№ 65. Решите уравнение х2+5у2+4ху+2у+1=0. В ответе укажите х+у.
а) 1; б) -1; в) 2; г) 3.
№ 66. Последовательность строится по следующему закону. На первом месте стоит число 7, далее за каждым числом стоит сумма цифр его квадрата, увеличенная на 1. Какое число стоит на 2000 месте?
а) 5; б) 20; в) 8; г) 11.
№ 67. Найти наименьшее натуральное число, дающее остатки: 1 – при делении на 2, 2 – при делении на 3, 3 - при делении на 4, 4 – при делении на 5, 5 – при делении на 6. В ответе укажите сумму цифр этого числа.
а) 14; б) 24; в) 11; г) 17.
№. 68. Решите уравнение Ix-2I+Ix-3I+I2x-8I=9. В ответе укажите произведение корней (если они есть).
а) 5,5; б) 5; в) 6,5; г) корней нет.
№ 69. Сторону квадрата уменьшили на 20%. На сколько процентов уменьшилась его площадь?
а) 36%; б) 20%; в) 10%; г) 40%.
№ 70. Семья состоит из мужа, жены и дочери. Если бы зарплата мужа увеличилась в двое, общий доход семьи вырос бы на 60%. Если бы стипендия дочери уменьшилась в двое, общий доход семьи уменьшился бы на 2%. Сколько процентов от общего дохода семьи составляет зарплата жены?
а) 36%; б) 30%; в) 28%; г) 32%
№ 71. В классе 21 шестиклассник, среди них два друга – Митя и Петя. Класс случайным образом делят на три группы, по 7 человек в каждой. Найдите вероятность того, что Митя и Петя окажутся в одной группе.
а) 0,3; б) 0,1; в) 0,2; г) 0,25.
№ 72. В кубе АВСDA1B1C1D1 найдите угол между прямой АВ1 и плоскостью АВС1.
а) 30ᵒ; б) 45ᵒ; в) 60ᵒ; г) 90ᵒ.
№ 73. У флориста (составителя букетов) имеются розы: 84 красные, 24 белые и 36 желтых. Какое наибольшее количество одинаковых букетов он может составить, если хочет использовать все имеющиеся розы?
а) 12; б) 4; в) 6; г) 18.
№ 74. Стрелок стреляет по мишени один раз. В случае промаха он делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,6. Найдите вероятность того, что мишень будет поражена.
а) 0,84; б) 0,36; в) 0,6; г) 0,8.
№ 75. Перед началом футбольного матча судья бросает монету, чтобы определить, какая команда будет владеть мячом. Команда «Меркурий» по очереди играет с командами «Марс», «Юпитер», «Уран». Найдите вероятность того, что во всех матчах право владеть мячом выиграет команда «Меркурий».
а) 0,125; б) 0,5; в) 1,5; г) 0,25.
№ 76. В кубе А…D1 точки К и М лежат на рёбрах ВВ1 и В1С1 соответственно, причём В1М:В1С1=В1К:В1В=0,6. Найдите угол между прямыми КМ и АС. Ответ дайте в градусах.
а) 60; б) 30; в) 45; г) 90.
№ 77. Два завода выпускают одинаковые автомобильные предохранители. Первый завод выпускает 40% предохранителей, второй – 60%. Первый завод выпускает 4% бракованных предохранителей, а второй – 3%. Найдите вероятность того, что случайно выбранных в магазине предохранитель бракованный.
а) 0,034; б) 0,24; в) 0,07; г) 0,34.
№ 78. Галя дважды бросила игральный кубик. Известно, то в сумме у неё выпало 9 очков. Найдите вероятность того, что при втором броске выпало 6 очков.
а) 0,25; б) 0,3; в) 0,54; г) 0,2.
№ 79. Четыре рубашки дешевле куртки на 20%. На сколько процентов шесть рубашек дороже куртки?
а) 20; б) 30; в) 40; г) рубашка и шесть курток стоят одинаково.
№ 80. Какое из следующих чисел является кубом натурального числа?
а) 6,4·1013; б) 6,4·1012; в) 6,4·1014; г) 6,4·1011.
№ 81. С полуночи до полудня Ученый Кот рассказывает сказки, а с полудня до полуночи – спит под дубом. На дубе том висит плакат: «Два часа назад Кот делал то же самое, что будет делать через час». В какой из указанных моментов времени надпись на плакате верна?
а) 22:30; б) 1:30; в) 23:30; г) 0:30.
№ 82. Пусть A= sin2 α + sin2 β, B = cos2 α + cos2 β. Какой из вариантов возможен?
а) А=3/4; В=5/4; б) А=1,5; В=4/3; в) А=2; В=2; г) А=1; В=1,5.
№ 83. Трапеция АВСD с основанием АВ вписана в окружность. Угол АDВ равен 65º, а угол DВС равен 35º. Тогда угол А равен
а) 75ᵒ; б) 80ᵒ; в) 70ᵒ; г) 105ᵒ.
№ 84. Если многоугольник (возможно, невыпуклый) составлен из 8 одинаковых правильных треугольников, то он не может быть
а) треугольником; б) трапецией; в) ромбом; г) шестиугольником.
№ 85. Сколько существует треугольников, у которых одна из сторон равна 3 см, другая – 4 см, а один из углов равен 10º?
а) 4; б) 3; в) 2; г) 1.
№ 86. Каждая пара вершин куба соединена отрезком. Сколько различных
середин у всех этих отрезков?
а) 19; б) 18; в) 12; г) 28.
№ 87. Вычислите 64-5/6-(0,125)-1/3-32·2-4·16-1,5+(30)4·4.
а) 2; б) -1; в) -2; г) 1.
№ 88. Дан куб А…D1. Через точки С, D1 и середину ребра АА1 проведена секущая плоскость. Найдите площадь сечения, если ребро куба равно 4.
а) 18; б) 16; в) 15,5; г) 15.
№ 89. Найдите расстояние от точки пересечения медиан прямоугольного треугольника до его гипотенузы, равной 25, если один из катетов 20.
а) 4; б) 12; в) 12,5; г) 5.
№ 90. В треугольнике ОВН точка М лежит на стороне ОВ, ОМ=4, МВ=28,
а) 16; б) 32; в) 8; г) 14.
№ 91. Дан куб А…D1. Через точки А, В1 и середину ребра СС1 проведена секущая плоскость. Найдите площадь полной поверхности куба, если площадь сечения равна 36.
а) 192; б) 32; в) 144; г) 216.
№ 92. Группа туристов в первый день путешествия прошла 10 км. Далее туристы решили ежедневно преодолевать на 5 км больше, чем в предыдущий день. В результате они преодолели расстояние 450 км. Сколько дней туристы были на маршруте, если в течении этого времени 8 дней они отдыхали?
а) 20; б) 12; в) 4; г) 18.
№ 93. Окружность разделена на 4 дуги, длины которых равны 2, 5, 6 и х. Дуга длины 2 соответствует центральному углу в 30º. Найдите величину х.
а) 11; б) 10; в) 9; г) 8.
№ 94. Скучая на уроке, отличник Петя заметил, что муха ползет по столу со
Скоростью 10000 миллиаршин в килосекунду. Один аршин равен 71 сантиметру. Определите скорость мухи в метрах в секунду.
а) 0,0071; б) 7,1; в) 0,071; г) 0,71.
№ 95. Сколько нечетных среди чисел 1015 ⋅1510 , 1515 +1010 , 1510 ⋅1515 , 1510+1515 ?
а) 2; б) 0; в) 1; г) 3.
№ 96. Окружности радиусов 3 см и 5 см расположены так, что у них ровно три общие касательные. Тогда расстояние между центрами окружностей
а) равно 8 см; б) меньше 2 см; в) равно 2 см; г) больше 8 см.
№ 97. Прямые y = 2x +3 и y = kx −3 пересекаются в первой четверти, причем ниже прямой y = 5. Тогда обязательно
а) k 8; б) 2k ≤5; в) ) 0 k ≤ 2; г) ) 5 k ≤8.
№ 98. Если n – число ребер некоторой призмы, то
а) n обязательно делится на 3; б) n может равняться 2006;
в) n обязательно четно; г) ) n обязательно нечетно.
№ 99. Если а = (11-12)13, то
а) а - положительно и близко к 0;
б) а – большое положительное число;
в) а – большое по модулю отрицательное число;
г) а - отрицательно и близко к 0.
№ 100. Пусть О – центр окружности, описанной около треугольника АВС. Найдите больший угол треугольника АВС, если АВОС – ромб.
а) 120º ; б) 100º; в) 110º; г) 150º.
№ 101. Семья Добсонов состоит из папы, мамы и нескольких детей. Средний
возраст членов семьи – 18 лет. Без 38-летнего папы средний возраст – 14 лет. Сколько детей в этой семье?
а) 4; б) 3; в) 2; г) 5.
№ 102. Какое самое маленькое значение может принимать периметр неравнобедренного треугольника с целыми длинами сторон?
а) 9; б) 6; в) 4; г) 3.
№ 103. В треугольнике АВС точка D – середина АВ, E – середина DВ, F – середина ВС. Если площадь треугольника АВС равна 96, то площадь треугольника АEF равна
а) 36; б) 32; в) 16; г) 48.
№ 104. При возведении в квадрат
а) изменяются все числа, кроме двух; б) число всегда изменяется;
в) изменяются все числа, кроме одного; г) число всегда увеличивается.
№ 105. Народная примета племени Уа-Уа гласит: «Если крокодилы едят быстро, то скоро будет дождь». Это означает, что
а) если дождя не ожидается, а крокодилы едят, то они едят не быстро;
б) если собирается дождь, то крокодилы едят быстро;
в) если крокодилы едят медленно, то дождя не будет;
г) если крокодилы воздерживаются от еды, то дождя не будет.
№ 106. Число 10100 назовем гигантом. Чему равно число 1000100?
а) гигант3; б) 100 гигантов; в) 3 гиганта; г) гигант2.
№ 107. ABCD – квадрат, а CDF – правильный треугольник. Чему равен угол BAF?
а) 75ᵒ; б) 60ᵒ; в) 85ᵒ; г) 67,5ᵒ.
№ 108. Прямоугольный треугольник таков, что длина его гипотенузы равна сумме квадратов длин его катетов. Чему равен радиус окружности, описанной около этого треугольника?
а) 1/2; б) 1; в) 2; г) такого треугольника не существует.
№ 109. Вася учится стрелять в тире. Месяц назад, на первом занятии, он попал 40 раз из 100. Сегодня, после месяца тренировок, он сделал 200 выстрелов и обнаружил, что его меткость (то есть доля удачных выстрелов) повысилась на 80%. Сколько раз он попал сегодня?
а) 144; б) 160; в) 120; г) 140.
№ 110. Маша сложила три числа: количество вершин, количество ребер и количество граней некоторой пирамиды. Какой результат она могла получить?
а) 30; б) 28; в) 29; г) 32.
№ 111. Решите уравнение (х+1)(х+2)(х+3)(х+4)=120. В ответе укажите произведение его корней
а) -6; б) 6; в) -96; г) корней нет.
№ 112. Укажите промежуток, которому принадлежит корень уравнения 2х4+5х3+6х2+5х+2=0.
а) [-1;0]; б) (0;1); в) [1;2]; г) корней нет.
№ 113. Вычислите х12·х2+х1··х22 , где х1 и х2 – корни уравнения х2-13х+2=0.
а) 26; б) 13; в) -13/2; г) корней нет.
№ 114. Среди нескольких различных простых чисел ровно n % делятся на 5. Чему не может равняться n ?
а) 15; б) 25; в) 20; г) 5.
№ 115. Решите уравнение I5-4xI+I2+4хI=7.
а) [-0,5; 1,25]; б) решений нет; в) (-0,5; 1,25); г) [0,5; 1,25].
№ 116. Решите уравнение I5-хI+I2+14хI=7-13х. В ответе укажите сумму его корней.
а) -2; б) 0; в) корней нет; г) 2.
№ 117. Найдите сумму целых решений неравенства х4-20х2+64
а) 0; б) 6; в) 3; г) -6.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
