Тема урока «Умножение многочлена на многочлен»
. С .

Самостоятельная работа
д) – 0,5c 2 ( c 3 + 2);
а) а ( х – у );
б) 2 p (3 – q );
е) –5 х (3 х 2 – 4);
в) –2 х ( х – 4);
ж) 2 a 4 ( а 3 – 0,5);
з) – q 7 ( q 3 – q 5 ).
г) 4 y ( у 3 + 0,25);

Самостоятельная работа
д) – 0,5c 2 ( c 3 + 2);
а) а ( х – у );
Ответ: ax-ay
Ответ: -0,5 c 5 - c 2
е) –5 х (3 х 2 – 4);
б) 2 p (3 – q );
Ответ: 6p-2pq
Ответ: -15х 3 +20x
в) –2 х ( х – 4);
ж) 2 a 4 ( а 3 – 0,5);
Ответ: -2 х 2 +8x
Ответ: 2 a 7 -a 4
з) – q 7 ( q 3 – q 5 ).
г) 4 y ( у 3 + 0,25);
Ответ: - q 10 + q 12
Ответ: 4 у 4 +y

Правило умножения многочленов
(а + b)(с + d) = ас + bс + аd + bd
(а + b)(с + d) = ас +аd + bс + bd
Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.

Изучение нового материала
( а + b ) ( c + d )
Обозначим двучлен ( a + b ) буквой х.
х ( c + d ) = x c +x d = ( a + b ) c + ( a + b ) d = ac + bc + ad + bd.
Итак, ( a + b ) ( c + d ) = ac + bc + ad + bd.
Чтобы умножить многочлен на многочлен, нужно
каждый член одного многочлена умножить
на каждый член другого многочлена и
полученные результаты сложить.

Алгоритм умножения многочлена на многочлен
1. Каждый член первого многочлена умножаем на каждый член второго многочлена
2. Полученные произведения складываем
3. Приводим подобные слагаемые

Пример 1 . Умножить многочлен (3 а – 2b ) на
многочлен (2 a + 3 b ).
Решение:
(3 a – 2 b )(2 a + 3 b ) =
= 3 a · 2 a + 3 a · 3 b + ( – 2 b ) · 2 a + (– 2 b ) · 3 b =
= 6 a 2 + 9 ab – 4 ab – 6 b 2
= 6 a 2 + 5 ab – 6 b 2 .
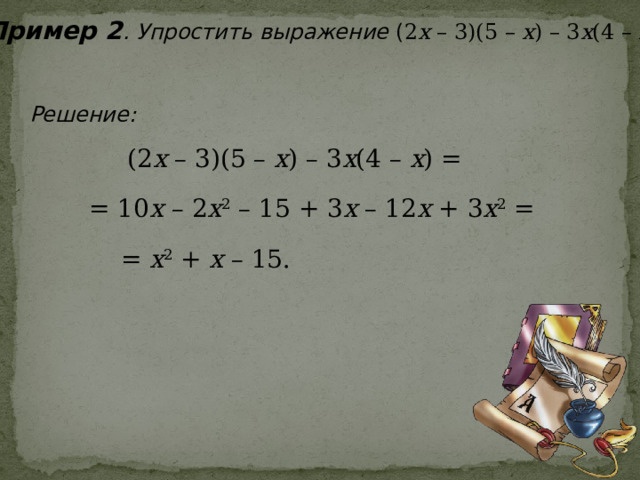
Пример 2 . Упростить выражение ( 2 х – 3)(5 – х ) – 3 х (4 – х ).
Решение:
(2 х – 3)(5 – х ) – 3 х (4 – х ) =
= 10 х – 2 х 2 – 15 + 3 х – 12 х + 3 х 2 =
= х 2 + х – 15.

Проверим!
1 вариант. (2а+3) ∙ (3а - 2) =
= 6а 2 – 4а +9а – 6 = 6а 2 +5а - 6
2 вариант. (4х+7) ∙ (2х-3) =
=8х 2 – 12х+ 14х – 21 = 8х 2 +2х – 21

Проверим!
1 вариант. (2а+3) ∙ (3а - 2) =
=
2 вариант. (4х+7) ∙ (2х-3) =

1. Сформулируйте правило умножения многочлена на многочлен.
Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные результаты сложить.
2.

Пример 3 . Докажем, что при любом натуральном
значении п значение выражения
( п + 1)( п + 2) – (3 п – 1)( п + 3) + 5 п ( п + 2) + п +7
кратно 3 .
Решение:
( п + 1)( п + 2) – (3 п – 1)( п + 3) + 5 п ( п + 2) + п +7 =
= п 2 + 2 п + п + 2 – 3 п 2 – 9 п + п + 3 + 5 п 2 + 10 п + п +7 =
3 ( п 2 + 2 п + 4).
= 3 п 2 + 6 п + 12 =
Вывод: При любом натуральном п произведение
3 ( п 2 + 2 п + 4) делится на 3, а значит и значение выражения
( п + 1)( п + 2) – (3 п – 1)( п + 3) + 5 п ( п + 2) + п +7
делится на 3.

Закрепление изученного
Учебник стр. 187,
№ 706
№ 707(а-г)
№ 708(а-г)
№ 709 (а,в)
№ 711 (а)

Домашнее задание
п. 7.4,
№ 707(д-з)
№ 708(д-з);
№ 709 (б, г)