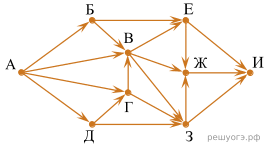
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город И, проходящих через город Г?

Решение.
Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.
При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчете сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.
С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:
А = 1.
Д = А = 1.
Г = А + Д = 2.
В = Г = 2. (А и Б не учитываем, поскольку путь должен проходить через Г)
Е = В = 2. (Б не учитываем, поскольку путь должен проходить через Г)
З = В + Г = 4. (Д не учитываем, поскольку путь должен проходить через Г)
Ж = В + Е + З = 8.
И = Е + Ж + З = 14.
Примечание. Необходимо найти количество различных путей из города А в город И, проходящих через город Г.
Приведем другое решение.
Количество путей из города А в город И, проходящих через город Г, равно произведению количества путей из города А в город Г и количества путей из города Г в город И.
Найдем количество путей из города А в город Г:
А = 1.
Д = А = 1.
Г = А + Д = 2.
Найдем количество путей из города Г в город И (при этом Г - исходный пункт):
Г = 1.
В = Г = 1.
Е = В = 1.
З = В + Г = 2.
Ж = В + Е + З = 4.
И = Е + Ж + З = 7.
Тогда количество путей из города А в город И, проходящих через город Г, равно 2 · 7 = 14.
Ответ: 14.
Просмотр содержимого документа
«Разбор задания ОГЭ по информатике. Декабрь 2024. Анализирование информации, представленной в виде схем. Поиск путей из одного города в другой, проходящих или не проходящих через определенный пункт»
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город И, проходящих через город Г?
Решение.
Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.
При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчете сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.
С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:
А = 1.
Д = А = 1.
Г = А + Д = 2.
В = Г = 2. (А и Б не учитываем, поскольку путь должен проходить через Г)
Е = В = 2. (Б не учитываем, поскольку путь должен проходить через Г)
З = В + Г = 4. (Д не учитываем, поскольку путь должен проходить через Г)
Ж = В + Е + З = 8.
И = Е + Ж + З = 14.
Примечание. Необходимо найти количество различных путей из города А в город И, проходящих через город Г.
Приведем другое решение.
Количество путей из города А в город И, проходящих через город Г, равно произведению количества путей из города А в город Г и количества путей из города Г в город И.
Найдем количество путей из города А в город Г:
А = 1.
Д = А = 1.
Г = А + Д = 2.
Найдем количество путей из города Г в город И (при этом Г - исходный пункт):
Г = 1.
В = Г = 1.
Е = В = 1.
З = В + Г = 2.
Ж = В + Е + З = 4.
И = Е + Ж + З = 7.
Тогда количество путей из города А в город И, проходящих через город Г, равно 2 · 7 = 14.
Ответ: 14.


















