Муниципальное казенное общеобразовательное учреждение
«Толпинская средняя общеобразовательная школа»
Урок алгебры
в 10 классе
«Показательная функция,
её свойства и график»
Дуплина Ирина Александровна
учитель математики, 1 категория
2020 – 2021 г
ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЁ СВОЙСТВА И ГРАФИК.
НЕКОТОРЫЕ НАИБОЛЕЕ ЧАСТО ВСТРЕЧАЮЩИЕСЯ
ВИДЫ ТРАНСЦЕНДЕНТНЫХ ФУНКЦИЙ ,
ПРЕЖДЕ ВСЕГО ПОКАЗАТЕЛЬНЫЕ,
ОТКРЫВАЮТ ДОСТУП КО МНОГИМ ИССЛЕДОВАНИЯМ.
л. ЭЙЛЕР
Цели:
Образовательные: повторение и закрепление учебного материала, коррекция, углубление, расширение знаний по теме «Показательная функция, ее свойства и график»: изучить основные свойства показательной функции; формировать умения использовать свойства показательной функции для исследования функций и решения уравнений и неравенств; включение в активную познавательную деятельность.
Развивающие: развитие графической культуры, математической речи, формирование алгоритма рефлексивного мышления.
Воспитательные: воспитание активности, самостоятельности, толерантности.
Тип урока: урок применения знаний на практике.
Форма: урок – практикум.
Ход урока
Организационный момент.
Здравствуйте, ребята. На предыдущем уроке мы начали изучение показательных функций. Сегодня мы продолжим работать с показательной функцией, исследовать её свойства, применять их на практике и ещё раз убедимся в справедливости высказывания Эйлера.
II. Устная работа.
1. Вычислить.
а) 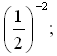 б) (–3)0; в)
б) (–3)0; в) 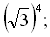
г) 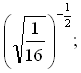 д) 037; е)
д) 037; е) 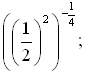
ж) 3–6 · 38; з) 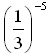 · 3–3; и)
· 3–3; и) 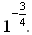
2. Среди заданных функций укажите те, которые являются показательными.
а) y = x3; б) y = 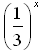 ; в) y =
; в) y = 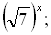
г) y = 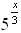 ; д) y = 8x2; е) y =
; д) y = 8x2; е) y = 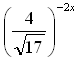 .
.
3. Найдите область определения функции:
а) у = а2х; б) у = 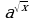 ; в) у =
; в) у = 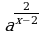 ; г) у =
; г) у = 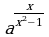 ; д) у =
; д) у = 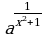 ; е) у =
; е) у = 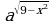 .
.
Ш. Расширение информационного поля учащихся. Применение показательной функции (работа по слайдам)
1У. Объяснение нового материала.
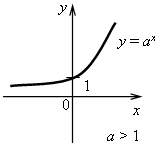
Перечислим основные свойства показательной функции y = ax. (вместе с учащимися по таблице).
1) D (f) = (–; +).
2) Ни четная, ни нечетная.
3) Монотонна. При 0 a a 1 – возрастает.
4) Ограничена снизу и не ограничена сверху.
5) Не имеет ни наименьшего, ни наибольшего значений.
6) Непрерывна.
7) E (f) = (0; +).
8) Выпукла вниз.
Рассмотренные свойства функции позволяют решать многие задачи, которые условно можно разбить на группы:
I группа. Нахождение значения функции для заданного аргумента и, наоборот, нахождение значения аргумента для заданного значения показательной функции.
II группа. Сравнение чисел, записанных в виде степени с действительным показателем. Сравнение показателей степеней при известном соотношении степеней.
III группа. Исследование показательной функции на монотонность, ограниченность, нахождение наибольшего и наименьшего значений функции.
IV группа. Графическое решение уравнений и неравенств вида
ax = b (ax b и др.)
IV. Формирование умений и навыков.
1. № 195 (устно).
При выполнении данного упражнения учащиеся должны назвать функцию, указать её вид, назвать её график. Следует оперировать такими понятиями как монотонность, ограниченность.
2. № 197(1,3).
При выполнении этого задания ученики должны обосновать выбор ключевых точек, единичного отрезка, расположение графика, возрастание (убывание).
3. № 199(1,3) 200(1,3)
При выполнении данных заданий используются свойства монотонности показательной функции.
№ 200
Все графики показательных функций проходят через точку с координатами (0; 1). Учащиеся могут изобразить соответствующие графики:
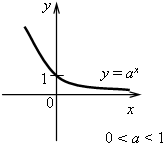
1) у = (1/3)х – убывающая (0
3) у = (5)х – возрастающая (5 1). Значит х1.
V. Проверочная работа.
Вариант 1
Найдите значение аргумента х, при котором функция у = 7х принимает значение, равное 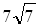 .
.
а ) 3/2 ; б)3; в)-2.
Сравните числа 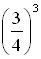 и
и 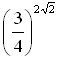 .
.
а)больше ; б)меньше ; в)равно.
Исследуйте на монотонность функцию y = 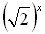 – 3.
– 3.
а)возрастает; б)убывает; в)не является ни возрастающей ни убывающей.
Вариант 2
Найдите значение аргумента х, при котором функция у = 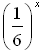 принимает значение, равное
принимает значение, равное 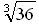 .
.
а)-2/3; б)2; в)2/3.
Сравните числа 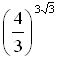 и
и 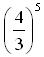 .
.
а)больше; б)меньше; в)равно.
Исследуйте на монотонность функцию y = –4x.
а)возрастает; б)убывает; в)не является ни возрастающей, ни убываюшей.
Вариант 3
Найдите значение аргумента х, при котором функция у = 5х принимает значение, равное 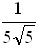 .
.
Сравните числа 1 и 0,23–0,5.
Исследуйте на монотонность функцию y =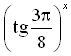 .
.
Вариант 4
Найдите значение аргумента х, при котором функция y = 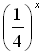 принимает значение, равное
принимает значение, равное 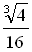 .
.
Сравните числа 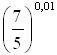 и 1.
и 1.
Исследуйте на монотонность функцию y =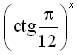 .
.
VI. Итоги урока.
Вопросы учащимся:
– Функция какого вида называется показательной?
– Назовите D (f) и E (f) функции у = ах.
– Каков характер монотонности показательной функции? Где она принимает наибольшее и наименьшее значения?
– Сформулируйте теоремы, изученные на этом уроке. На каком свойстве показательной функции они основаны?
Домашнее задание: параграф 11, №194(1,2), №199(2,4),№200(2,4)






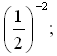 б) (–3)0; в)
б) (–3)0; в) 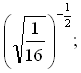 д) 037; е)
д) 037; е) 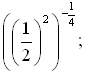
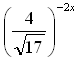 .
.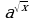 ; в) у =
; в) у = 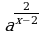 ; г) у =
; г) у = 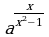 ; д) у =
; д) у = 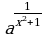 ; е) у =
; е) у = 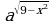 .
.

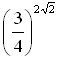 .
.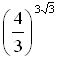 и
и 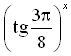 .
.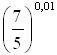 и 1.
и 1.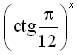 .
.









