20.04.20 ДО-193б математика

Тема: « Понятие объема. Свойства объема.

Объем прямоугольного параллелепипеда»

Цель занятия: Ввести понятие объема тела, рассмотреть свойства объемов, теорему об объеме прямоугольного параллелепипеда и следствие об объеме; сформировать умение применять данный материал при решении задач.

ХОД ЗАНЯТИЯ

1. Организационный момент

Сообщение темы и целей занятия, актуальность данной темы

1. Актуализация знаний

Что называется параллелепипедом? прямоугольным параллелепипедом? Какие свойства прямоугольного параллелепипеда вы знаете?

III. Объяснение нового материала

1) Понятие объема тела

Еще в глубокой древности у людей возникла необходимость в измерении количества различных веществ. Сыпучие вещества и жидкости можно было мерить, наполняя ими сосуды определенной вместимости, т.е. определяя их количество по объему. Понятие объема в стереометрии вводится аналогично понятию площади в планиметрии. В планиметрии мы определяли площадь так: площадь многоугольника – это величина той части плоскости, которую занимает многоугольник. Сформулировать аналогично данному понятию понятие объема. Величина части пространства, занимаемого геометрическим телом, называется объемом этого тела.

2) Единицы измерения объема

В повседневной жизни нам часто приходится определять объемы различных тел. Например, коробки, банки. В житейской практике единицами объема служили меры емкости, используемые для хранения сыпучих и жидких тел.
Среди них английские меры:

• Бушель – 36,4 дм³

• Галлон – 4,5 дм³

• Баррель (сухой) – 115,628 дм³

• Баррель (нефтяной) – 158,988 дм³

• Английский баррель для сыпучих веществ 163,65 дм³.

В Киевской Руси существовала мера зерна – кадь. ( Это примерно 230 кг ржи) Жидкости же мерили бочками и ведрами. В XIX в. система мер жидкости имела вид:

• Ведро – 12 дм³

• Бочка – 490 дм³

• Штоф – 1,23 дм³ = 10 чарок

• Чарка – 0,123 дм³=0,1 штофа = 2 шкалика

• Шкалик – 0,06 дм³ = 0,5 чарки.

Для того, чтобы определить какая из двух емкостей вместительнее, можно заполнить одну из них водой, а затем проверить, вся ли вода поместится в другую, и если вся, то заполнит ли она ее полностью. Однако решить эту задачу иначе – вычислить объем каждой емкости. Для этого нам нужны единицы объемов. Когда в планиметрии мы вводили единицы площади, то за единицу площади брали квадрат со стороной 1 см (1 см²). Аналогично, за 1см³ принимаем куб с ребром 1 см. Процедура измерения объемов аналогична процедуре измерения площадей. Число измерения (единичных кубов) и частей единицы, содержащихся в данном теле, принимается за числовое значение объема при выбранной единице измерения. Это число может быть как рациональным (в частности, целым), так и иррациональным.

3) Свойства объемов

Аналогичны свойствам площадей в планиметрии.

1. Равные тела имеют равные объемы. (Понятие определяется на основе понятия наложения).

2. Объем тела, состоящего из некоторых частей, равен сумме объемов этих частей.

3. Объем куба с ребром а равен а³.

4) Объем прямоугольного параллелепипеда

Поиск формул, позволяющих вычислять объемы различных тел, был долог.
В древнеегипетских папирусах, в вавилонских клинописных табличках встречаются правила для нахождения объема усеченной пирамиды, но не сообщаются правила для вычисления объема полной пирамиды.
Определять объемы призмы, пирамиды, цилиндра и конуса умели древние греки еще задолго до Архимеда. Но только он имел общий метод, позволяющий определить любую площадь или объем. Идеи Архимеда легли в основу интегрального исчисления. Сам ученый определил с помощью своего метода площади, объемы почти всех тел, которые рассматривались в античной математике. На могильной плите Архимеда, как завещал ученый, был изображен цилиндр с вписанным шаром, а эпитафия говорила о величайшем открытии Архимеда – о том, что объемы этих тел относятся как 3 : 2.Когда Римский оратор и общественный деятель Цицерон, живший в 1 в. до н.э., был в Сицилии, он еще видел этот заросший кустами и терновником памятник с шаром и цилиндром.

Мы будем находить объем прямоугольного параллелепипеда, используя следующую теорему ( давно знакомая вам формула, попробуйте сформулировать эту теорему):

Теорема: Объем прямоугольного параллелепипеда равен произведению трех его измерений.

V = abc

5) Следствия

Рассмотрим следствия из данной теоремы

1. Объем прямоугольного параллелепипеда, равен произведению площади основания на высоту.

IV. Закрепление

1. Учащиеся получают модели прямоугольных параллелепипедов, нужно выполнить нужные измерения, вычислить диагональ и объем данного параллелепипеда.

2. Решение задач

Задача 1

Сколько пакетов с соком войдет в коробку?

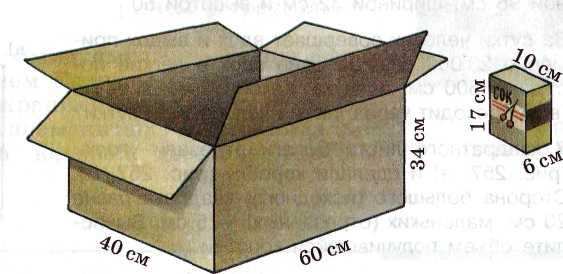
Задача 2

Найдите объем тела:

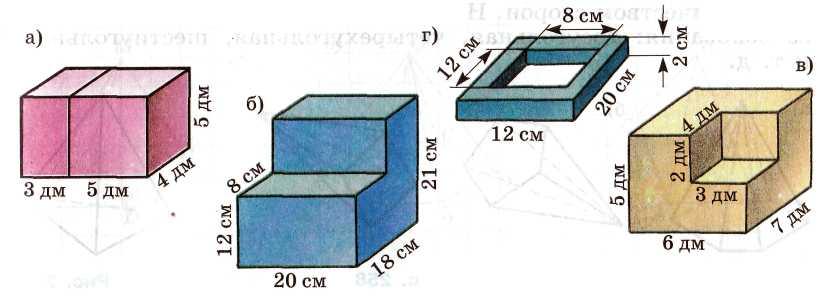
Задача 3

Сколько литров воды вмещает бак, имеющий форму куба с ребром 6 дм?

Задача 4

За сутки человек совершает вдох и выдох примерно 23 000 раз. За один вдох в легкие поступает 500 см³ воздуха. Какой объем воздуха (в литрах) проходит через легкие человека за сутки?

Задача 5

Больному прописали глазные капли, по 2 капли 3 раза в день в оба глаза. Во флаконе 10 мл лекарства. Объем капли 1/9 мл. Хватит ли одного флакона на неделю?

Задача 6. Измерения прямоугольного параллелепипеда равны 8 см, 12 см и 18 см. найдите ребро куба, объем которого равен объему этого параллелепипеда.

Учащиеся решают данную задачу на листочках, затем в рабочую тетрадь записывают только ответ, а листок с решением сдают учителю. После этого решение с ответом отображается на экране, учащиеся проверяют свое решение и ответ.

Задача 7. Диагональ прямоугольного параллелепипеда равна 18 см и составляет угол в 30° с плоскостью боковой грани и угол в 45°с боковым ребром. Найдите объем прямоугольного параллелепипеда.

Учащиеся на местах обдумывают решение, затем один выходит к доске и демонстрирует решение.

Решение задач из учебного пособия №134, 137, 138, 145

V. Итог занятия

Что такое объем тела? Какие единицы измерения вы знаете? Какие свойства объема вы знаете? Сформулируйте теорему о объеме прямоугольного параллелепипеда и следствия из нее.

VI. Домашнее задание

• Гл.2 §1, №135, 147 Выучить основные определения и теоремы

Дополнительное задание(для дистанционного обучения)

• !Придумать задачу с практическим содержанием на нахождение объема прямоугольного параллелепипеда, решить ее.

• ! Сделать модель прямоугольного параллелепипеда, найти его длину, ширину, высоту, диагональ, объем