4
§18. Функциялар
18.1. Функциянын аныктамасы
Эгерде Х көптүгүнүн ар бир х элементине У көптүгүнүн бир гана у элементи туура келсе, анда у өзгөрмө чоңдугу х өзгөрмө чоңдугунун функциясы деп аталат жана y=f(x) деп белгиленет. Х көптүгүнүн элементтери көз каранды эмес өзгөрмөлөр же аргумент деп аталат, ал эми у көз каранды өзгөрмө же функция деп аталат. Х көптүгүнүн элементтери функциянын аныкталуу областы же жашоо областы деп аталат да 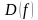 деп белгиленет. У көптүгүнүн элементтери функциянын маанилеринин көптүгү деп аталат да
деп белгиленет. У көптүгүнүн элементтери функциянын маанилеринин көптүгү деп аталат да 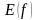 деп белгиленет.
деп белгиленет.
№18.1. 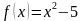 ,
, 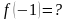
№18.2. 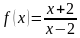 ,
, 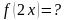
№18.3. 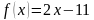 функциясы х тин кандай маанисинде 7 ге барабар?
функциясы х тин кандай маанисинде 7 ге барабар?
№18.4. 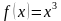 функциясынын
функциясынын 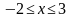 интервалындагы маанилеринин көптүгүн тапкыла.
интервалындагы маанилеринин көптүгүн тапкыла.
№18.5. Функциялардын аныкталуу аймагын тапкыла: 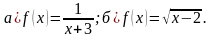
18.2. Жуп жана так функциялар
Эгерде y=f(x) функциясынын аныкталуу аймагынын ар бир х мааниси үчүн,
-
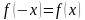 барабардыгы орун алса,
барабардыгы орун алса, 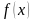 функциясы жуп;
функциясы жуп;
-
 барабардыгы орун алса,
барабардыгы орун алса, 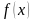 функциясы так функция деп аталат.
функциясы так функция деп аталат.
№18.6. Берилген функцияларды аныкталуу аймагында так же жуп экендигин аныктагыл:
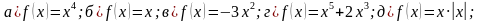
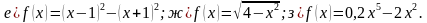
18.3. Өсүүчү жана кемүүчү функциялар
Эгерде Х интервалында каалагандай 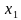 жана
жана 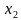 маанилери
маанилери 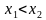 болсо жана
болсо жана
-
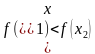 барабарсыздыгы орун алса, анда
барабарсыздыгы орун алса, анда 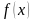 функциясы Х интервалында өсүүчү
функциясы Х интервалында өсүүчү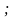
-
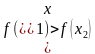 барабарсыздыгы орун алса, анда
барабарсыздыгы орун алса, анда 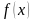 функциясы Х интервалында кемүүчү;
функциясы Х интервалында кемүүчү;
-
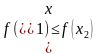 барабарсыздыгы орун алса, анда
барабарсыздыгы орун алса, анда 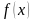 функциясы Х интервалында кемибөөчү;
функциясы Х интервалында кемибөөчү;
-
барабарсыздыгы орун алса, анда 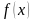 функциясы Х интервалында өсбөөчү деп аталат
функциясы Х интервалында өсбөөчү деп аталат
Өсүүчү жана кемүүчү функцияларды монотондуу функциялар дейбиз.
18.4. Татаал функциялар
Эгерде у чоңдугу и дан функция болуп, ал эми и функциясы х тен функция болсо, б.а.  болсо, анда у чоңдугу х тен татаал функция болот дейбиз да
болсо, анда у чоңдугу х тен татаал функция болот дейбиз да  жазабыз. У чоңдугу көз каранды болбогон х аргументинен татаал функция, ал эми и арадагы аргумент деп аталат.
жазабыз. У чоңдугу көз каранды болбогон х аргументинен татаал функция, ал эми и арадагы аргумент деп аталат.  татаал функциясы
татаал функциясы  функциясынын аныкталуу областына кирүүчү
функциясынын аныкталуу областына кирүүчү  функциясындагы х тин маанилери үчүн гана аныкталат.
функциясындагы х тин маанилери үчүн гана аныкталат.
Эскертүү.
№18.7. болсо, анда  жана
жана  ти тапкыла.
ти тапкыла.
№18.8. болсо, анда  ди тапкыла.
ди тапкыла.
18.5. Тескери функция
Эгерде  функциясы берилип, х өзгөрмөсү у өзгөрмөсү аркылуу туюнтулса, анда
функциясы берилип, х өзгөрмөсү у өзгөрмөсү аркылуу туюнтулса, анда  функциясына
функциясына  тескери функция болот. Бирок х тамгасы менен аргументти, ал эми у аркылуу функцияны белгилөө көнүмүш болгондуктан,
тескери функция болот. Бирок х тамгасы менен аргументти, ал эми у аркылуу функцияны белгилөө көнүмүш болгондуктан,  тамгасы менен белгиленген функциялык көз карандылыкты
тамгасы менен белгиленген функциялык көз карандылыкты  түрүндө жазууга болот. Ошентип,
түрүндө жазууга болот. Ошентип,  функциясына тескери болгон
функциясына тескери болгон  функциясын чыгаруу үчүн
функциясын чыгаруу үчүн  теңдемесин х ке карата чыгаруу керек.
теңдемесин х ке карата чыгаруу керек.
Мисалы,  барабардыгында у тин ар бир маанисине х тин
барабардыгында у тин ар бир маанисине х тин  мааниси туура келет. Демек,
мааниси туура келет. Демек, функциясы
функциясы  функциясына тескери функция.
функциясына тескери функция.
 функциясы Х аралыгында аныкталып, өссө (же кемисе) жана маанилеринин областы У аралыгы болсо, анда У аралыгында аныкталуучу жана өсүүчү (кемүүчү) татаал функция болот.
функциясы Х аралыгында аныкталып, өссө (же кемисе) жана маанилеринин областы У аралыгы болсо, анда У аралыгында аныкталуучу жана өсүүчү (кемүүчү) татаал функция болот.
№18.9. Берилген функцияга тескери функцияны тапкыла:
18.6. Функциянын түрлөрү
1) Турактуу функция.  түрүндөгү функцияны турактуу функция дейбиз турактуу функциянын графиги абсцисса огуна параллель болуп (0; с) чекити аркылуу өткөн түз сызык болот. Мисалы, ж.б. турактуу функциялар.
түрүндөгү функцияны турактуу функция дейбиз турактуу функциянын графиги абсцисса огуна параллель болуп (0; с) чекити аркылуу өткөн түз сызык болот. Мисалы, ж.б. турактуу функциялар.
2) Түз пропорционалдуулук.  формуласы менен берилген функция түз пропорционалдуу функция деп аталат. k саны пропорционалдуулук коэффициенти деп аталат. Түз пропорционалдуу функциянын касиеттери:
формуласы менен берилген функция түз пропорционалдуу функция деп аталат. k саны пропорционалдуулук коэффициенти деп аталат. Түз пропорционалдуу функциянын касиеттери:
- аныкталуу областы, чыныгы сандардын көптүгү - ℝ;
- функция так функция, себеби, 
-  болсо, функция бардык сан огунда өсүүчү;
болсо, функция бардык сан огунда өсүүчү;  болсо, функция бардык сан огунда кемүүчү;
болсо, функция бардык сан огунда кемүүчү;
- түз пропорционалдуу функциянын графиги түз сызык болот.
3) Сызыктуу функция.  формуласы менен берилген функцияны сызыктуу функция дейбиз. Мында
формуласы менен берилген функцияны сызыктуу функция дейбиз. Мында  жана
жана  чыныгы сандар. Сызыктуу функциянын касиеттери:
чыныгы сандар. Сызыктуу функциянын касиеттери:
- аныкталуу областы, чыныгы сандардын көптүгү - ℝ ;
- функция жуп да, так да эмес;
-  болсо, функция бардык сан огунда өсүүчү;
болсо, функция бардык сан огунда өсүүчү;  болсо, функция бардык сан огунда кемүүчү;
болсо, функция бардык сан огунда кемүүчү;
- сызыктуу функциянын графиги түз сызык болот.
4) Тескери пропорционалдуулук.  формуласы менен берилген функцияны тескери пропорционалдуу функция дейбиз. k саны пропорционалдуулук коэффициенти деп аталат. Тескери пропорционалдуу функциянын касиеттери:
формуласы менен берилген функцияны тескери пропорционалдуу функция дейбиз. k саны пропорционалдуулук коэффициенти деп аталат. Тескери пропорционалдуу функциянын касиеттери:
- аныкталуу областы, нөл чекитинен башка чыныгы сандардын көптүгү - ℝ
- функция так,
-  болсо, функция ℝ
болсо, функция ℝ интервалында өсүүчү,
интервалында өсүүчү,  болсо, функция ℝ
болсо, функция ℝ интервалында кемүүчү;
интервалында кемүүчү;
- координата октору функциянын графигинин вертикалдуу жана горизонталдуу асимптоталары болот;
- тескери пропорционалдуу  функциясынын графигин гипербола дейбиз.
функциясынын графигин гипербола дейбиз.
5) Кубдук функция  Касиеттери:
Касиеттери:
- аныкталуу областы, чыныгы сандардын көптүгү - ℝ;
- функция так;
- функция бүткүл сан огунда өсүүчү;
- функциянын графиги кубдук парабола.
6)  түрүндөгү функция. Касиеттери:
түрүндөгү функция. Касиеттери:
- аныкталуу областы - 
- функция так да, жуп да эмес;
- функция возрастает на луче 
7) Рационалдуу функциялар. Рационалдык функциясынын аныкталуу областы  функциясынын аныкталуу областы жана
функциясынын аныкталуу областы жана  функциясынын
функциясынын  болгон маанилеринен башка маанилеринин көптүгү
болгон маанилеринен башка маанилеринин көптүгү
№18.10. Функциялардын аныкталуу областарын тапкыла:
8) Рационалдуу көрсөткүчтүү функциялар.  түрүндөгү функция рационалдык көрсөткүчтүү функция деп аталат. Рационалдык көрсөткүчтүү функциянын аныкталуу областы:
түрүндөгү функция рационалдык көрсөткүчтүү функция деп аталат. Рационалдык көрсөткүчтүү функциянын аныкталуу областы:
- эгерде п – так сан болсо, анда  функциясынын аныкталуу областы;
функциясынын аныкталуу областы;
- эгерде п – жуп сан болсо, анда  барабарсыздыгынын чечими.
барабарсыздыгынын чечими.
№18.11. Функциялардын аныкталуу областарын тапкыла:
ТЕСТ «ФУНКЦИЯЛАР»
ВАРИАНТ «А»
| № | Тесттин материалдары | Жооптору |
| 1 | Функциянын аныкталуу областын тапкыла: | А)  Б)  В)  Г)  Д)  |
| 2 | Функциянын аныкталуу областын тапкыла: | А) (0;2] Б) В)  Г) [3; Д)  |
| 3 | Чиймеде кайсыл функциянын графиги сызылган? 
| А)  Б)  В)  Г)  Д)  |
| 4 | Так функцияны тапкыла. | А) Б) В) Г) Д) |
| 5 | Аргумент х тин кайсыл маанисинде  функциясынын мааниси 15ке барабар? функциясынын мааниси 15ке барабар? | А) 36 Б) 56 В) - 56 Г) - 84 Д) 32 |
| 6 | Келтирилген функциялардын кайсынысы сызыктуу функция? | А)  Б)  В)  4 4 Г)  Д)  |
| 7 | Функциянын аныкталуу областын тапкыла: | А)  Б)  В) ℝ Г)  Д)  |
| 8 | Функциянын аныкталуу областын тапкыла: 
| А)  Б)  В)  Г)  Д)  |
| 9 | Функциянын маанилеринин көптүгүн тапкыла: | А)  Б)  В)  Г)  Д)  |
| 10 | Функциянын аныкталуу областын тапкыла: | А) [1;7] Б) [-5;2)∪(2;7) В) [-5;5] Г) [-5;2)∪(2;5] Д) ( |
| 11 | Функциянын аныкталуу областын тапкыла: | А) [0;1) Б) [3;+ В) [1;3)∪(3;+ Г)  Д)  |
| 12 | Берилген функцияга тескери функцияны тапкыла: 
| А)  Б)  В)  Г)  Д)  |
| 13 | Берилген функцияга тескери функцияны тапкыла: | А)  Б)  В)  Г)  Д)  |
| 14 | Берилген функцияга тескери функцияны тапкыла: 
| А)  Б)  В)  Г)  Д)  |
| 15 | Берилген функцияга тескери функцияны тапкыла: 
| А)  Б)  В)  Г)  Д)  |
| 16 | Функциянын аныкталуу областын тапкыла: | А)  Б)  В)  Г)  Д)  |
| 17 | Кайсыл функция үчүн  барабардыгы орун алат? барабардыгы орун алат? | А)  Б)  В)  Г)  Д)  |
| 18 | Аргумент х тин кандай маанисинде  мааниси 25 кеи барабар? мааниси 25 кеи барабар? | А)  Б)  В)  Г)  Д)  |
| 19 |  функциясы берилген. Төмөнкү чекиттердин кайсынысы функциянын графигинде жатат? функциясы берилген. Төмөнкү чекиттердин кайсынысы функциянын графигинде жатат?
| А)  Б)  В)  Г)  Д) |
| 20 | Эгерде  болсо, анда болсо, анда | А)  Б)  В) 89. Г) 504 Д) 65 |
| 21 | Эгерде  жана болсо, анда жана болсо, анда | А) 0 Б) 7 В) 10 Г) 21 Д) 25 |
| 22 | Берилген функциянын аныкталуу областынын канча бүтүн мааниси бар? | А) 0 Б) 5 В) 10 Г) 11 Д) чексиз көп |
| 23 | Эгерде  жана жана  болсо, анда болсо, анда  | А) 1 Б) 2 В) 3 Г) 4 Д) 5 |
| 24 | Эгерде  жана жана  болсо, анда болсо, анда  | А)  Б) 520 В) 680 Г) 1120 Д) 1280 |
| 25 | Эгерде  жана жана  болсо, анда болсо, анда  | А)  Б)  В)  Г) 1 Д) 5 |
ТЕСТ «ФУНКЦИЯЛАР»
ВАРИАНТ «Б»
| № | Тесттин материалдары | Жооптору |
| 1 | Функциянын аныкталуу областын тапкыла: 
| А)  Б)  В)  Г) ℝ Д)  |
| 2 | Тескери функцияны тапкыла:  | А)  Б)  В)  Г)  Д)  |
| 3 | Функциянын аныкталуу областын тапкыла: | А)  Б) В)  Г)  Д)  |
| 4 | Функциянын аныкталуу областын тапкыла: | А)  Б)  В)  Г)  Д)  |
| 5 | Эгерде  болсо, анда болсо, анда  | А) 2 Б) 4 В) 8 Г) 16 Д)  |
| 6 | Функциянын аныкталуу областын тапкыла: | А)  Б)  В)  Г)  Д)  |
| 7 | Функциянын аныкталуу областын тапкыла: | А)  Б)  В)  Г)  Д)  |
| 8 | Эгерде  болсо, анда болсо, анда  | А)  Б)  В) 96. Г) 54 Д) 65 |
| 9 | Функциянын аныкталуу областын тапкыла: | А)  Б)  В)  Г)  Д)  |
| 10 | Функциянын аныкталуу областын тапкыла: 
| А)  Б)  В)  Г)  Д)  |
| 11 | Функциянын аныкталуу областында канча бүтүн чечими бар? | А) 0 Б) 7 В) 10 Г) 9 Д) чексиз көп |
| 12 | Функциянын маанилеринин көптүгүн тапкыла: 
| А)  Б)  В)  Г)  Д)  |
| 13 | Функциянын маанилеринин көптүгүн тапкыла: 
| А)  Б)  В)  Г)  Д)  |
| 14 | Функциянын  чекитиндеги маанисин тапкыла: чекитиндеги маанисин тапкыла: 
| А)  . . Б)  . . В)  Г) 4. Д) 5. |
| 15 |  жана жана  функциялары берилген. функциялары берилген. | А)  Б)  В)  Г)  Д)  |
| 16 |  жана жана  функциялары берилген. функциялары берилген.
| А)  Б)  В)  Г)  Д)  |
| 17 | Функциянын аныкталуу областын тапкыла: | А)  Б)  В)  Г)  Д)  |
| 18 | Сызыктуу  функциясынын графиги функциясынын графиги  чекити аркылуу өтөт. чекити аркылуу өтөт.  | А)  Б)  В)  Г)  Д)  |
| 19 |  функциясы берилген. Төмөнкүлөрдүн кайсынысы дайыма туура: функциясы берилген. Төмөнкүлөрдүн кайсынысы дайыма туура:
-
-
функция  интервалында кемүүчү; интервалында кемүүчү; -

-

| А) 1; 3 Б) 2; 3 В) 1; 2; 3; 4 Г) 1; 2; 4 Д) 1; 2 |
| 20 | Функцияга тескери функцияны тапкыла: 
| А)  Б)  В)  Г)  Д)  |
| 21 | Функцияга тескери функцияны тапкыла: | А)  Б)  В)  Г)  Д)  |
| 22 | Эгерде  жана жана  болсо, анда болсо, анда  | А)  Б) 56 В) 68 Г) 112 Д) 128 |
| 23 | Бул кандай функция?  | А) так да, жуп да эмес. Б) так. В) мезгилдүү. Г) жуп. Д) жалпы түрдөгү функция. |
| 24 | Бул функциялардын кайсынысы так функция? -

-

-

-

-

| А) 1; 4 Б) 1; 2; 3 В) 2; 4; 5 Г) 1; 3; 4 Д)1; 5 |
| 25 | Функцияга тескери функцияны тапкыла: | А)  Б)  В)  Г)  Д)  |







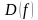 деп белгиленет. У көптүгүнүн элементтери функциянын маанилеринин көптүгү деп аталат да
деп белгиленет. У көптүгүнүн элементтери функциянын маанилеринин көптүгү деп аталат да 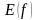 деп белгиленет.
деп белгиленет.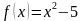 ,
, 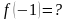
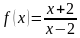 ,
, 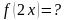
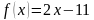 функциясы х тин кандай маанисинде 7 ге барабар?
функциясы х тин кандай маанисинде 7 ге барабар?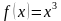 функциясынын
функциясынын 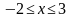 интервалындагы маанилеринин көптүгүн тапкыла.
интервалындагы маанилеринин көптүгүн тапкыла.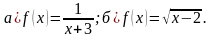
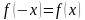 барабардыгы орун алса,
барабардыгы орун алса, 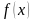 функциясы жуп;
функциясы жуп; барабардыгы орун алса,
барабардыгы орун алса, 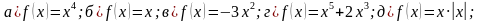
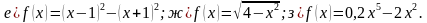
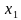 жана
жана 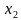 маанилери
маанилери 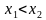 болсо жана
болсо жана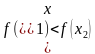 барабарсыздыгы орун алса, анда
барабарсыздыгы орун алса, анда 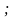
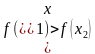 барабарсыздыгы орун алса, анда
барабарсыздыгы орун алса, анда 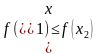 барабарсыздыгы орун алса, анда
барабарсыздыгы орун алса, анда 




















