Развитие функциональной математической грамотности обучающихся 5-9 классов

Конкурс методических материалов среди

стажировочных площадок по формированию и оценке функциональной грамотности

обучающихся образовательных организаций

Ханты-Мансийского автономного округа - Югры

Номинация

«Лучшая методическая разработка урока/внеурочного мероприятия, направленного на формирование, развитие и оценку функциональной грамотности обучающихся основной и средней школы»

Тема методической разработки

Развитие функциональной математической грамотности

обучающихся 5-9 классов

Автор: Петрачкова Ирина Анатольевна,

учитель математики

муниципального автономного общеобразовательного учреждения

«Средняя общеобразовательная школа №1»

города Покачи Ханты-Мансийского автономного округа - Югры

2024 г.

Введение 3

1. Развитие математической грамотности обучающихся основной школы через использование готовых разработок 4

2. Развитие математической грамотности обучающихся основной школы через собственные разработки 5

Заключение 7

Список литературы 8

Приложения 9

Приложение 1 9

Приложение 2 12

Приложение 3 13

Данная работа посвящена развитию функциональной математической грамотности обучающихся 5-9 классов. Начинать работу над формированием функциональной грамотности детей необходимо в дошкольном возрасте и в начальной школе, а в основной школе надо продолжать развивать навыки, приобретенные ранее.

Для чего это надо? Прежде всего, потому что одной из приоритетных целей федеральной рабочей программы основного общего образования по математике является «формирование функциональной математической грамотности: умение распознавать математические объекты в реальных жизненных ситуациях, применять освоенные умения для решения практико-ориентированных задач, интерпретировать полученные результаты и оценивать их на соответствие практической ситуации» [1].

Но не менее важным фактором (а может быть и более важным) является то, что в постоянно меняющемся мире для того, чтобы быть востребованным на рынке труда, современному человеку, помимо профессиональных навыков, надо уметь быстро адаптироваться к происходящим изменениям и иметь гибкое математическое мышление.

Иначе говоря, дети (как будущие самостоятельные члены общества) должны быть функционально грамотными, в том числе и математически. С активно развивающимися технологиями математическая грамотность становится незаменимой для активного участия людей в социальной, культурной, политической и экономической деятельности, а также обучению на протяжении всей жизни. Это и является актуальностью данной работы.

Цель методической разработки: описать опыт работы по развитию функциональной математической грамотности обучающихся через использование готовых банков заданий или заданий, разработанных самостоятельно.

Задачи:

• Показать необходимость формирования математической грамотности обучающихся основной школы;

• Обозначить категории контекстов и виды заданий для формирования математической грамотности;

• Использовать рекомендации при самостоятельной разработке заданий по функциональной грамотности;

• Научить создавать задания интересные и близкие детям.

Предполагаемые результаты разработки: представленные задания можно использовать на уроках математики; по данным в работе рекомендациям можно самостоятельно разрабатывать задания с учетом интересов обучающихся.

1. Развитие математической грамотности обучающихся основной школы через использование готовых разработок

По терминологии международного исследования PISA под математической грамотностью понимается «способность учащегося использовать математические знания, приобретенные им за время обучения в школе, для решения разнообразных задач межпредметного и практико-ориентированного содержания, для дальнейшего обучения и успешной социализации в обществе».

Важной составляющей математической грамотности является использование математики при решении различных проблем. То есть математическая интуиция и математические знания должны использоваться в различных жизненных ситуациях. Причем наиболее близкими для учащихся являются темы, связанные с личной повседневной жизнью, со школой, спортом, социумом. Все перечисленные темы определяют 4 категории контекстов, выделяемых разработчиками заданий формата, в качестве ключевых, которые должны стать близкими и понятными учащимся – это «количество», «изменения и зависимости», «пространство и форма», «неопределенность и данные».  

Для решения ситуационной задачи математически грамотный учащийся сначала должен увидеть математическую природу проблемы, представленной в контексте реального мира, затем сформулировать ее на языке математики, применить знания, умения и навыки, оценить полученные результаты.

Но не все дети могут быстро выделить проблему из текста задачи и сформулировать ее на математическом языке. Трудности, с которыми сталкиваются дети при решении функциональных заданий: это и объемные тексты заданий (дети порой только от вида заданий начинают паниковать), в которых еще и возможна лишняя информация, и неявный вид математического содержания, и сочетание различных рассуждений.

Какие задания надо использовать, чтобы помочь детям справиться с трудностями и формировать у них математическую грамотность?

Это задания, которые содержат:

• Распознавание и нахождение значений величин.

• Оценку утверждений.

• Построение и обоснование математической модели.

• Интерпретацию.

Существует достаточное количество ресурсов, на которых в свободном доступе есть банки заданий по формированию и оценке функциональной грамотности обучающихся, такие как Российская электронная школа, Институт стратегии развития образования, ФИОКО, Медиатека Просвещения, Учи.ру и многие другие. Кроме этого, издательство Просвещение выпустило сборники эталонных заданий по функциональной грамотности, в частности по математической грамотности, а также в открытом доступе есть сборники заданий формата PISA, где можно найти замечательные задания как для проведения урока, так и внеурочного занятия. Я этими ресурсами активно пользуюсь, начиная с 5 класса, и конечно при подготовке к основному государственному экзамену для отработки умения детей решать задачи с практическим содержанием.

1. Развитие математической грамотности обучающихся основной школы через собственные разработки

Безусловно, каждый учитель математики может самостоятельно разрабатывать задания, направленные на формирование математической грамотности обучающихся, опираясь на жизненный опыт своих учеников и уровень их развития. Но при этом необходимо учитывать следующие рекомендации.

Структура и содержание конструируемых заданий должны включать три основных блока:

• контекст, в котором представлена проблема, положенная в основу задания;

• математические умения, которые используются обучающимися при выполнении заданий;

• мыслительная деятельность, необходимая для того, чтобы связать контекст, в котором представлена проблема, с математическими навыками, необходимыми для её решения.

При разработке контекста задания следует учитывать особенности реального окружения учащихся, используя их в рамках предлагаемой ситуации. Жизненные ситуации необходимо связывать с разными аспектами окружающей школьника реальности, требующими для решения проблем применения математического аппарата.

Математическое содержание, на основе которого целесообразно разрабатывать задания по формированию математической грамотности, должно быть представлено следующими блоками: пространство и форма, изменение и зависимости, количество, неопределённость и данные. Именно они помогут школьникам решать проблемы контекстных заданий, описывающих жизненные ситуации. Эти блоки есть в школьном курсе математики, и они необходимы для обеспечения базовых основ формирования функциональной грамотности обучающихся. Уровень освоения этих умений позволит оценить возможности учащихся при использовании полученных знаний в повседневной жизни.

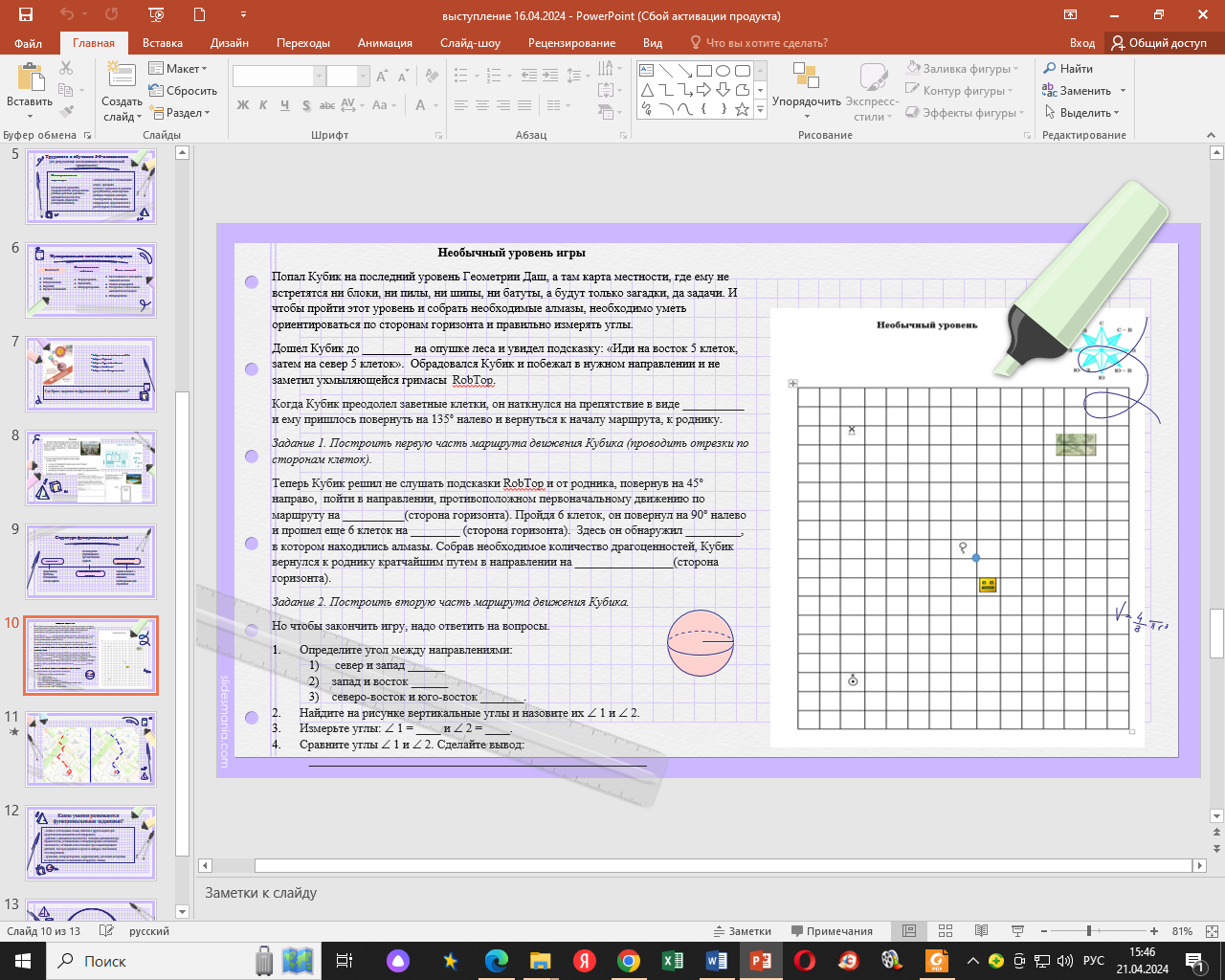
Рисунок 1.

Я тоже пробую составлять подобные задания, с учетом интересов детей. Задание, представленное на рисунке 1, я составила при закреплении темы «Углы» в 5 классе после посещенного урока географии в моем классе. Мои ученики, как и наверняка многие, на переменах не выпускали из рук свои гаджеты, играли в компьютерные игры. Я выяснила, что самая популярная игра у моих учеников – это Геометрия Даш. И поэтому ее главный герой Кубик также является основным персонажем в разработанном мной задании, которого дети встретили с восторгом. А также их заинтересовал формат задания, разработанного по принципу прохождения квеста (полный текст задания в Приложении 1).

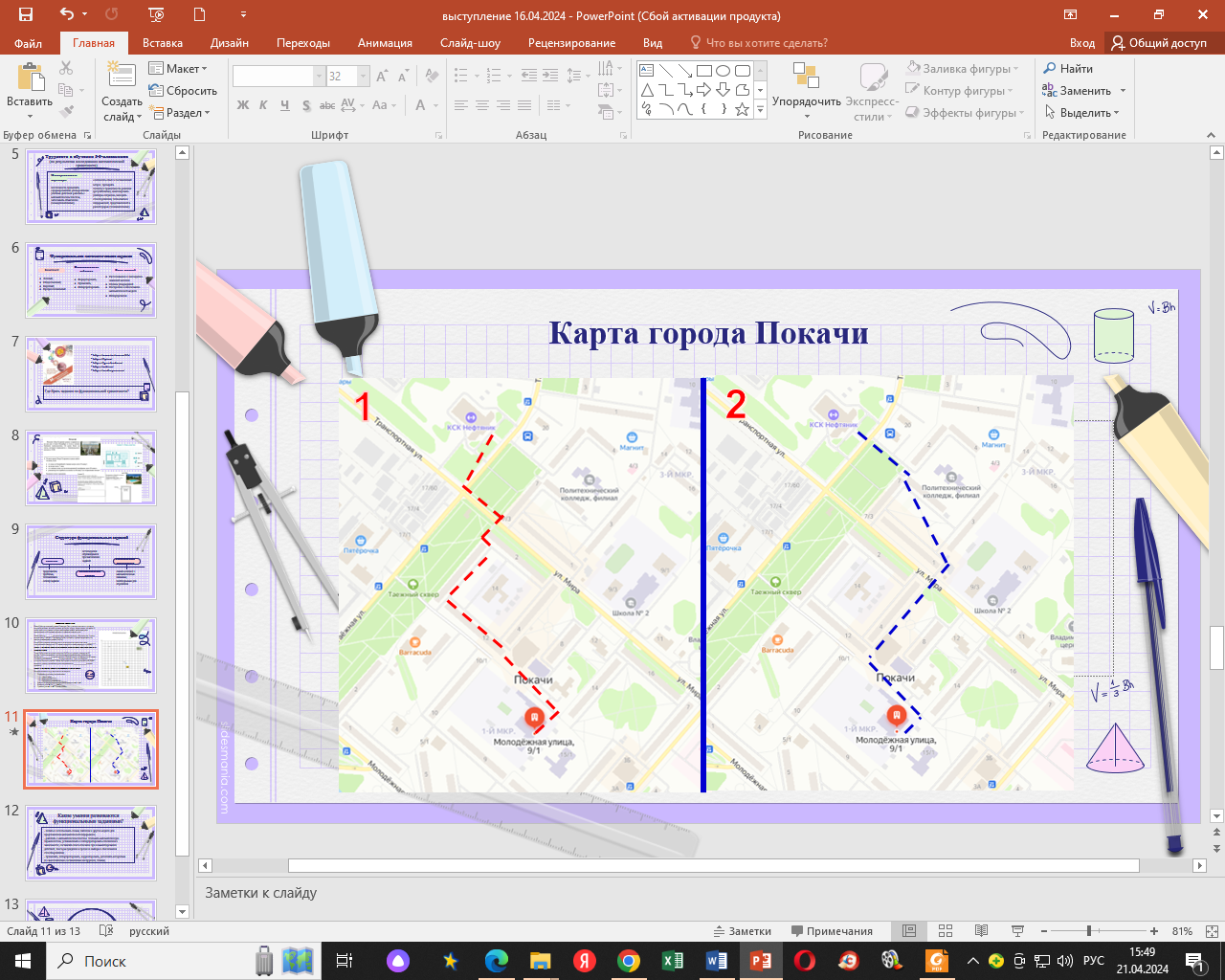
Рисунок 2.

А задание, представленное на рисунке 2, я составила по геометрии в 7 классе при повторении темы «Неравенство треугольника. Свойства прямоугольных треугольников». Идея пришла после смотра строя и песни, который мы проводили в КСК (культурно-спортивный комплекс). По дороге с детьми спорили о длине выбранного маршрута. И в этом задании детям было предложено сначала на глаз определить, какой из двух различных маршрутов короче, затем измерить их и проверить свои предположения. А самое главное, объяснить, опираясь на геометрический материал, почему (текст задания в Приложении 2).

Кроме этого, полезно также и детям пробовать себя в роли разработчиков собственных заданий. Это могут быть загадки, ребусы, текстовые задачи и прочее. Мой ученик Бардачев Данил, когда был в 6 классе, создал интерактивную презентацию-путешествие по теме «Проценты» (Приложение 3).

Какие умения развиваются у обучающихся подобными функциональными заданиями?

Дети учатся:

• читать и использовать схемы, таблицы и другие модели для представления математической информации;

• работать с математическим текстом: понимать математическую терминологию; устанавливать и интерпретировать отношения и зависимости; составлять текст-описание при комментировании действий, текст-рассуждение в процессе выбора и обоснования способа решения;

• применять, интерпретировать, корректировать, дополнять алгоритмы (и самостоятельно составленные инструкции, планы).

В данной работе представлена характеристика заданий по формированию математической грамотности обучающихся, которые я использую на своих уроках математики, а также ресурсы, на которых можно взять готовые материалы, либо составить собственные с учетом предлагаемых рекомендаций. Несмотря на узкую направленность разработанных мной заданий на интересы моих детей, представленными материалами в данной работе могут воспользоваться другие учителя при изучении указанных тем школьного курса математики.

Опытом формирования и развития функциональной грамотности я регулярно делюсь с коллегами на заседаниях ШМО, ГМО, педагогических советах, городских семинарах и других методических мероприятиях. Так, 29 апреля 2022 года я представляла свой опыт на региональном методическом совещании; в апреле 2023 года проводила городской хакатон по разработке заданий, способствующих формированию и развитию функциональной грамотности; в апреле 2024 года поделилась накопленным опытом на городском фестивале инновационных практик по формированию и развитию функциональной грамотности; моя статья по математической грамотности вошла в сборник материалов «Формирование функциональной грамотности обучающихся: эффективные практики педагогов и образовательных организаций Ханты-Мансийского автономного округа – Югры», Ханты-Мансийск 2022.

В заключение хочется отметить, что независимо от того, где были взяты задания (из готового банка заданий по формированию функциональной грамотности или составлены самостоятельно), главное, чтобы они решали основную задачу – это обучение учащихся умению видеть математическую природу жизненных проблем, формулировать выявленные проблемы на языке математики, применять известные математические понятия, процедуры, рассуждения, интерпретировать и оценивать математические результаты с учетом контекста решаемых задач. Систематизированная совокупность этих умений определяет содержание математической грамотности учащихся, которая является необходимым условием их успешного функционирования в настоящем и будущем.

1. Федеральная образовательная программа основного общего образования. Федеральная рабочая программа по учебному предмету «Математика» (базовый уровень). – утверждена Минпросом РФ от 18.05.2023 г. № 370.

2. Открытые задания PISA. [сайт].– URL:  https://fioco.ru/.

3. Открытый банк заданий для формирования функциональной грамотности. Математическая грамотность. 5 класс. 6 класс. 7 класс. 8 класс. 9 класс. /Сост. ИСРО РАО Министерства просвещения РФ, 2020.

4. Открытый банк заданий для формирования функциональной грамотности. [сайт].– URL: https://fg.resh.edu.ru/ .

5. Ковалева Г.С. Математическая грамотность. Сборник эталонных заданий. Выпуск 1. В 2 частях. Часть 1, Часть 2. ФГОС. – М.: Просвещение, 2024.

Необычный уровень игры

Попал Кубик на последний уровень Геометрии Даш, а там карта местности, где ему не встретятся ни блоки, ни пилы, ни шипы, ни батуты, а будут только загадки, да задачи. И чтобы пройти этот уровень и собрать необходимые алмазы, необходимо уметь ориентироваться по сторонам горизонта и правильно измерять углы.

Дошел Кубик до ________ на опушке леса и увидел подсказку: «Иди на восток 5 клеток, затем на север 5 клеток». Обрадовался Кубик и побежал в нужном направлении и не заметил ухмыляющейся гримасы  RobTop.

Когда Кубик преодолел заветные клетки, он наткнулся на препятствие в виде __________ и ему пришлось повернуть на 135° налево и вернуться к началу маршрута, к роднику.

Задание 1. Построить первую часть маршрута движения Кубика (проводить отрезки по сторонам клеток).

Теперь Кубик решил не слушать подсказки RobTop и от родника, повернув на 45° направо, пойти в направлении, противоположном первоначальному движению по маршруту на __________(сторона горизонта). Пройдя 6 клеток, он повернул на 90° налево и прошел еще 6 клеток на ________ (сторона горизонта). Здесь он обнаружил _________, в котором находились алмазы. Собрав необходимое количество драгоценностей, Кубик вернулся к роднику кратчайшим путем в направлении на ________________(сторона горизонта).

Задание 2. Построить вторую часть маршрута движения Кубика.

Но чтобы закончить игру, надо ответить на вопросы.

1. Определите угол между направлениями:

1. север и запад ______

2. запад и восток ______

3. северо-восток и юго-восток _______.

1. Найдите на рисунке вертикальные углы и назовите их  1 и  2.

2. Измерьте углы:  1 = ____ и  2 = ____.

3. Сравните углы  1 и  2. Сделайте вывод:

_______________________________________________________

Victory! Game over!

К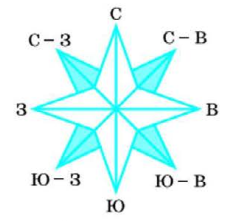 арта местности

Помогатор

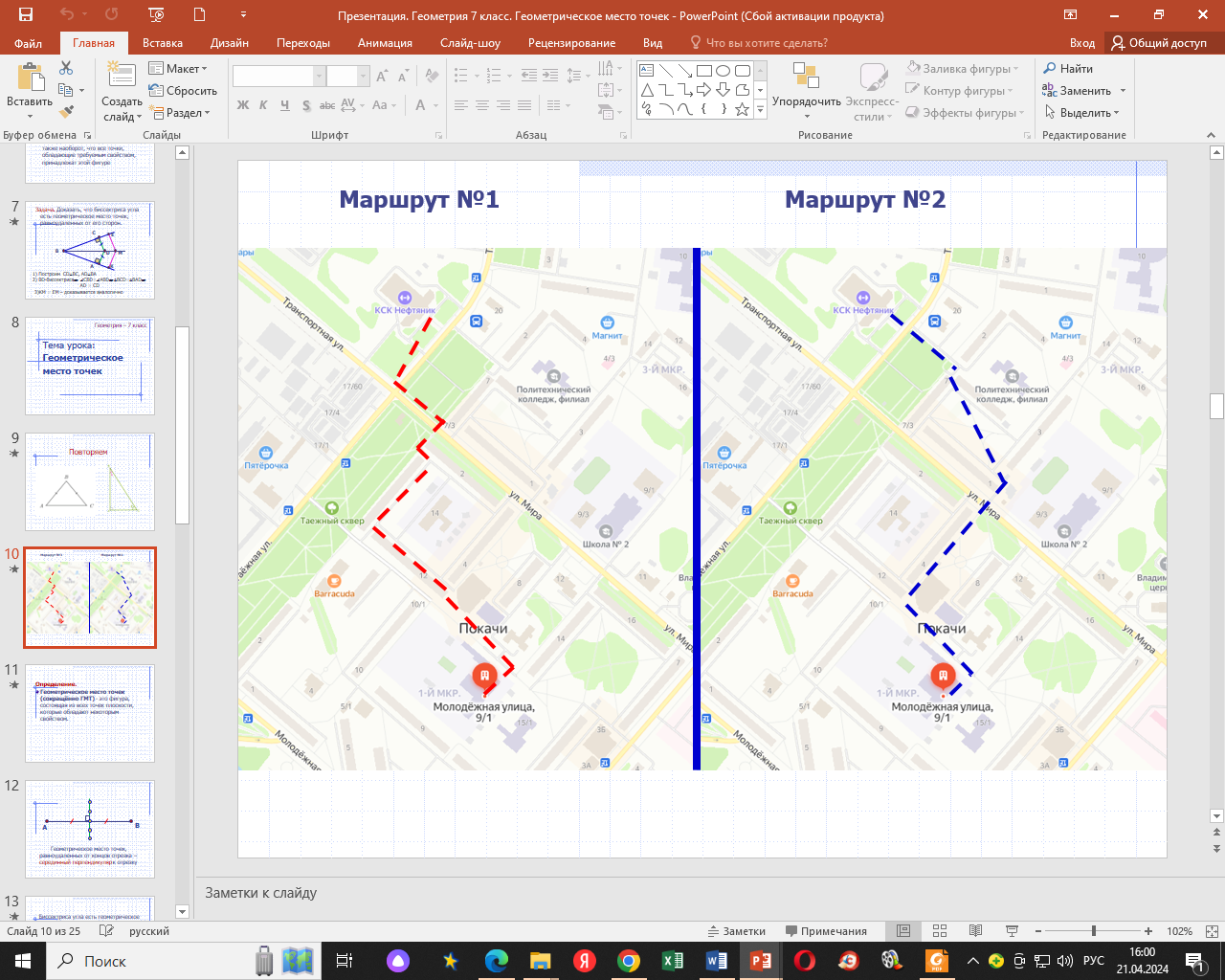
Перед вами представлен фрагмент карты города Покачи и два различных маршрута, как можно пройти от нашей школы до КСК. Выполните задания и ответьте на предложенные вопросы.

1. Определите «на глаз»: какой из маршрутов короче?

2. С помощью линейки измерьте длины маршрутов и сделайте соответствующие выводы.

3. С учетом масштаба карты 1:500 найдите, на сколько метров маршрут №2 короче маршрута №1.

4. Опираясь на геометрический материал, объясните, почему маршрут №2 короче маршрута №1.