Тема. Решение дробных рациональных уравнений. Обобщение и систематизация темы: «Уравнения, виды уравнений и способы их решения»
Цели обучения Образовательная:
- систематизировать и обобщить знания обучающихся об уравнениях;
- расширить и обобщить знания обучающихся по теме – решение дробных рациональных уравнений, используя при этом различные приемы и методы.
- повторить различные способы решения дробных рациональных уравнений.
- продолжить обучение решению дробных рациональных уравнений по алгоритму решения дробных рациональных уравнений. - провести проверку уровня усвоения темы путем проведения самостоятельной работы.
Развивающая:
- развитие коммуникативных навыков общения и умения слушать и слышать;
- развитие умения правильно оперировать полученными знаниями, логически мыслить;
- развитие интеллектуальных умений и мыслительных операций - анализ, синтез, сравнение и обобщение;
- развитие инициативы, умения принимать решения, не останавливаться на достигнутом;
Воспитательная:
- воспитание познавательного интереса к предмету;
- стимулировать самостоятельную деятельность, способствовать формированию коммуникативных навыков. - воспитание воли и упорства для достижения конечных результатов. Цель урока: - обеспечить осознанное усвоение обучающимися алгоритма решения дробно-рациональных уравнений;
- активизировать мыслительную деятельность школьников через активное участие каждого в процессе работы.
Тип урока: Урок систематизации и обобщения знаний и умений.. Методы и технологии, используемые на уроке: проблемно-поисковые, словесные практические, ИКТ, групповые, технология развития критического мышления, технология коллективной мыслительной деятельности (КМД)
Технология креативного мышления «Шесть думающих шляп». Оборудование и наглядность: базовый учебник Макарычев Ю.Н. Алгебра. 9 класс: учеб. Для обучающихся общеобразовательных учреждений. «Просвещение», 2014г; ноутбук, дополнительный раздаточный материал. Ресурсы: презентация «Решение дробных рациональных уравнений», наборы шляпок, кластеры уравнений, раздаточный материал для рефлексии.
| Планируемые результаты | Личностные | Метапредметные | Предметные |
| умение понимать смысл поставленной задачи, критичность мышления
| Познавательные: понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом Регулятивные: целеполагание, планирование, контроль, коррекция, оценка Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли
| Формирование навыка решения рациональных уравнений, умения работать с текстом задачи; грамотно использовать математическую терминологию и символику. |
| Основные понятия
| Линейное уравнение, квадратное уравнение, полное, неполное, алгоритм решения линейного и квадратного уравнения, рациональное уравнение, решение дробных рациональных уравнений и алгоритм решения дробно- рациональных уравнений. |
Ход урока
І.Организационный момент.
Добрый день, ребята! Запишите дату в тетрадях и тему урока: « Решение дробных рациональных уравнений»
Девиз урока
Покоряет вершины тот,
кто к ним стремится
.Установка на успех
1.Определи для себя значение данного материала. 2.Наметь цель и не отступай от неё. 3. Радуйся, когда тебе удастся достичь хотя бы маленького успеха. 4. Не огорчайся, если с первого раза не удастся. Попробуй ещё раз. 5. Не бойся попросить помощи. 6. Спрашивай, если в чём-то сомневаешься. 7. Я верю, что каждый из вас справится.
Успехов вам!
II.Проверка домашнего задания, воспроизведение и коррекция опорных знаний обучающихся. Актуализация знаний
-
Двое учащихся работают у доски (решение упражнений аналогичных домашним)
-
При каких значениях a равно нулю значение дроби:
а)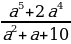 ; Ответ :0 б)
; Ответ :0 б) 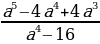 . Ответ: 0 (Работа в диалоге)
. Ответ: 0 (Работа в диалоге)
2. Остальные учащиеся проверяют выполнение домашнего задания, применяя «Инсерт»
3. Проверь себя ( Слайд )
Пример 1.
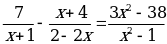
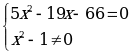
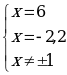
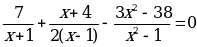
Общий знаменатель 2(x+1)(х -1) =2( х2 -1)
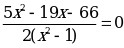
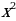
x1 =6, x2= - 2,2. Ответ: -2,2 ;6.
Пример 2.
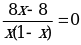
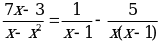
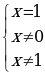 нет решений
нет решений
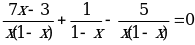

Общий знаменатель х(1-х)
Ответ: нет решений
.
П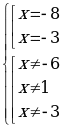 ример 3.
ример 3.
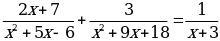
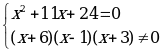
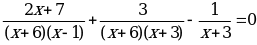
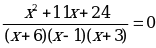 x = -8 ОДЗ: х
x = -8 ОДЗ: х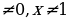
Ответ: -8.
4. Решите устно:
а) 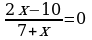 ; б)
; б) 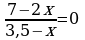 ; в)
; в) 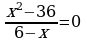 .
.
Ответ: а) 5; б) корней нет; в) – 6.
5. Проверка кластеров «Уравнения, виды и способы их решений»
III. Постановка цели и задач урока. Мотивация учебной деятельности обучающихся.
Сегодня на уроке мне хотелось бы вас пригласить поглубже заглянуть в замечательный мир математики – в мир уравнений, в мир поиска, в мир исследований.

Слово учителя о преемственности при изучении темы «Уравнения, виды и способы их решений»
Уравнения в школьном курсе математике занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Подавляющее большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.).
IV.Обобщение и систематизация знаний по теме «Уравнения, виды и способы их решений»
1.Начальная школа
В период обучения в начальной школе формируются базовые знания, умения и навыки, на основе которых будет строиться дальнейшее изучение математики. Начальная школа занимает решающее место: проблема преемственности может не возникнуть только в случае, когда правильно организованно начальное обучение. Другими словами, на начальную школу возлагается высочайшая ответственность за все дальнейшее обучение математики. Вот почему так важно дать учащимся наиболее полную информацию о сущности уравнения и показать им пути его решения.
2 класс «Знакомство с уравнениями. Решение уравнений методом подбора»
- Ребята, посмотрите, пожалуйста, на доску. Вам знакома такая запись?
+ 4 = 12 (Да, это пример с «окошком»)
- А такая: а + 4? (Да, это буквенное выражение)
- Что вы делали в первом случае? (подбирали число, чтобы запись была верной)
- Что делали во втором случае? (Вместо буквы подставляли числа и вычисляли).
- А сейчас внимательно посмотрите на запись, которую принёс нам Знайка Математик.
х + 4 = 12
- На что она похожа? (И на пример с «окошечком» и на буквенное выражение).
- Что нам говорит знак «=»? (Это равенство)
- Какое равенство? Все числа в нём известны? (нет).
- Что неизвестно? (первое число)
- Как оно обозначено? (латинской буквой)
- Если оно неизвестно, перед нами какая встаёт задача? (Найти, узнать какое это число)
- Найдите это число, чтобы равенство было верным. (Это число 8, потому что 8 + 4 = 12)
- А знаете, что вы сейчас сделали? Вы решили уравнение х+4=12
- Попробуем сделать вывод из всего сказанного и сделанного. Уравнение это (учитель показывает знак «=») (Равенство)
- Которое содержит что (показываю на х)? (Неизвестное число)
- Что надо сделать с неизвестным числом? (Его надо найти)
- Как обозначается неизвестное число? (Латинской буквой)
- Кто может сказать, что такое уравнение? (Уравнение – это равенство, которое содержит неизвестное число)
- Что значит «решить уравнение»? Найти такое число, чтобы равенство было верным)
- Давайте решим уравнения (3 человека у доски)
8 + х = 14 13 - х = 7 a – 5 = 9
- Как нашли неизвестное число? ( Дети рассказывают алгоритм: 1) Чтобы найти неизвестное слагаемое, надо из суммы вычесть другое слагаемое.
2) Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность. 3) Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое).
. Итог урока.
- Ребята, вот и близится к концу наш урок. С каким математическим понятием мы познакомились? (Мы познакомились с понятием «уравнение»)
- Тогда скажите, что же такое уравнение?
(Равенство, которое содержит неизвестное число).
- А что значит решить уравнение?
(Решить уравнение – значит найти неизвестное число, чтобы равенство было верным).
3 класс
– Что такое уравнение? (Равенство, содержащее неизвестное число, которое надо найти).
Самоопределение к деятельности
– Среди записей найдите уравнение.
38 + х 74 – 18 = 56 х + 6 3
46 + 12 = 58 х – 8 = 63 х – 22
– Как вы догадались? (Ответы детей)
– Давайте вспомним, как называются компоненты при вычитании? Что нам нужно найти? Какое правило поможет нам найти уменьшаемое? (Чтобы найти неизвестное уменьшаемое нужно к разности прибавить вычитаемое). Решите уравнение.
х – 8 = 63
х = 63 + 8
х = 71
71 – 8 = 63
63 = 63
– Как вы думаете, чем мы будем заниматься сегодня на уроке?
– Совершенно верно. Мы продолжим учиться решать уравнения.
Или:
1. Повторение связи между суммой и слагаемыми.
5+7=12
-Давай вспомним компоненты при сложении( Слагаемое, слагаемое, сумма)
-Что такое 5? (Первое слагаемое)
-Что такое 7? (Второе слагаемое)
-Что такое 12? (Сумма).
-Что необходимо сделать, чтобы найти неизвестное первое слагаемое? (Нужно из суммы вычесть второе слагаемое). 12-7=5
-Что необходимо сделать, чтобы найти второе слагаемое? (Надо из суммы вычесть первое слагаемое). 12—5=7
4 класс
алгоритм действий по решению простых уравнений
· Прочитать уравнение.
· Определить, что неизвестно в уравнении.
· Применить правило нахождения неизвестного слагаемого.
· Произвести вычисления.
· Сделать проверку.
Алгоритм решения сложного уравнения.
1)Прочитать уравнение.
2) Упростить правую часть уравнения.
3)Определить, что неизвестно.
4)Применить правило нахождение неизвестного слагаемого.
5)Произвести вычисления.
6)Сделать проверку.
24 + Х = 79 – 30
24+x=49
X=25
24+25=79-30
49=49
- Понятие об уравнении
Способы решения уравнений:
а) способ подбора;
б) решение уравнений на основе зависимости между компонентами действий.
в) решение уравнений на основе соотношения между частью и целым.
г) решение уравнений на основе знаний конкретного смысла умножения.
2. 5-6 классы
3. 7-8 классы
7 класс
1.Уравнения с одной переменной или с одним неизвестным
а).Что такое уравнение? (Равенство, содержащее неизвестное).
б).Что такое корень уравнения? (Значение переменной, при котором уравнение обращается в верное равенство).
в).Что значит решить уравнение? (Значит найти все его корни или доказать, что их нет).
2. Линейное уравнение
Уравнение вида ах =в , где х – переменная , а и в - некоторые числа , называется линейным уравнением с одной переменной .
Уравнение вида ах =в при а 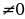 имеет один корень,
имеет один корень,
при а=0, в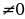 не имеет корней,
не имеет корней,
при а =0 , в= 0 имеет бесконечно много корней ( любое число является его корнем)
-
класс
1.Квадратные уравнения
Квадратным уравнением называется уравнение вида 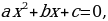 где x - переменная, а , в и с – некоторые числа, причём а
где x - переменная, а , в и с – некоторые числа, причём а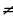 0.
0.
а , в и с – коэффициенты КУ, число а – называется первым коэффициентом, число в – вторым коэффициентом и число с – свободным членом.
Степень уравнения вида 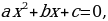 ( наибольшая степень переменной х – квадрат), поэтому – квадратное уравнение.
( наибольшая степень переменной х – квадрат), поэтому – квадратное уравнение.
Квадратное уравнение, в котором коэффициент при 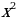 равен 1, называется приведенным квадратным уравнением.
равен 1, называется приведенным квадратным уравнением.
Квадратное уравнение, в котором хотя бы один из коэффициентов b или с равен нулю, называют неполным квадратным уравнением.
Неполные квадратные уравнения бывают трёх видов:
-
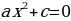 , где с
, где с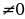 ;
;
-
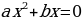 , где в
, где в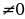
-
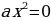 .
.
Выражение 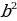 - 4ac называют дискриминантом квадратного уравнения и его обозначают буквой D =
- 4ac называют дискриминантом квадратного уравнения и его обозначают буквой D =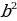 - 4ac
- 4ac
Если D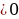 , уравнение имеет два корня,
, уравнение имеет два корня,
Если D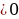 , то уравнение не имеет корней,
, то уравнение не имеет корней,
Если D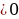 , то уравнение имеет один корень.
, то уравнение имеет один корень.
Формулы корней КУ:
1. 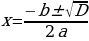 , где D =
, где D =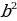 - 4ac,
- 4ac,
2. 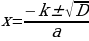 , где D =
, где D =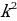 - ac для квадратного уравнения
- ac для квадратного уравнения 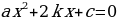 ,
,
3.Теорема Виета - сумма корней квадратного уравнения 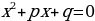 равна второму коэффициенту, взятому с противоположным знаком, т.е. х1 + х2 = -
равна второму коэффициенту, взятому с противоположным знаком, т.е. х1 + х2 = -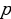 ,
,
а произведение корней равно свободному члену, т.е. х1 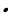 х2 =
х2 = 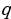 ..
..
2.Дробные рациональные уравнения
Выражения, составленные из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля, называют целыми выражениями.
Выражения, помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменной, называются дробными выражениями
Целые и дробные выражения называют рациональными выражениями.
Что является допустимым значением рациональной дроби (допустимым значением рациональной дроби являются те значения переменных, при которых не обращается в нуль знаменатель дроби)
Уравнения, в которых левая и правая части являются рациональными выражениями, называются рациональными уравнениями.
Рациональное уравнение, в котором левая или правая часть является дробным выражением, называют дробным.
Рациональное уравнение, в котором левая или правая часть является целым выражением, называют целым.
Способы решения дробно- рациональных уравнений:
1.Исползование свойство дроби равной нулю,
2.Использование свойства дроби, равной 1,
3. Использование свойства пропорции,
4.Введение новой переменной.
4 . 9 класс
Какое уравнение с одной переменной называется целым (целым уравнением с одной переменной называется уравнение, левая и правая части которого - целые выражения)
Дайте определение биквадратного уравнения (уравнение вида 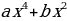 + c = 0, где
+ c = 0, где 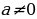 являющемся квадратным относительно
являющемся квадратным относительно 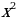 , называется биквадратным уравнением).
, называется биквадратным уравнением).
Какое уравнение называется дробным рациональным (дробным рациональным уравнением называется уравнение, обе части которого являются рациональными выражениями, причём хотя бы одно из них – дробным выражением).
Какие существует способов решения дробных рациональных уравнений:
1.Приведение дробей к общему знаменателю;
2.Умножение дробей на общий знаменатель всех дробей.
3. Графический способ;
4. Введение новой переменной;
5.Выделение из дробей целой части)
Когда дробь равна нулю (дробь равна нулю когда числитель равен нулю, а знаменатель не равен нулю)
Первый алгоритм решения дробных рациональных уравнений:
1. Находят общий знаменатель дробей, входящих в уравнение.
2. Умножают обе части уравнения на этот знаменатель.
3.Решают получившееся целое уравнение.
4.Исключают из его коней те, которые обращают в нуль общий знаменатель дроби.
5. Записываем ответ.
Второй алгоритм решения дробных рациональных уравнений:
-
Найти допустимые значения дробей, входящих в уравнение.
-
Найти общий знаменатель дробей, входящих в уравнение.
-
Умножить обе части уравнения на общий знаменатель.
-
Решить получившееся уравнение.
-
Исключить корни, не входящие в допустимые значения дробей уравнения.
Обобщая весь теоретический материал, хочу вас спросить:
Какие виды уравнений вы знаете? Определение. (линейные, квадратные и приводимые к квадратным, дробные, целые, рациональные , дробно- рациональные)
Когда в уравнении появляются посторонние корни?
V.Применение знаний и умений в новой ситуации




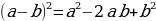
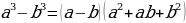
VI.Контроль усвоения, обсуждение допущенных ошибок и их коррекция
3.71. Тракторист должен был вспахать за некоторое время поле площадью 180 га. Но ежедневно он вспахивал на 2 га больше, чем планировал, поэтому закончил работу на 1 день раньше срока. За сколько дней тракторист вспахал поле?
Во время объяснения задачи применяем технологию «Шесть думающих шляпок»
1.Надеваем белую шляпу – и собираем информацию, которая у нас имеется.
А имеется …… проговариваем условие задачи…...
Необходимо определить ……. За сколько дней тракторист вспахал поле?
А как это сделать? …… Площадь поля разделить на количество гектар, которые он вспахивал каждый день
2. Надеваем черную шляпу – ребята, рассмотрим, какие имеются недостатки, проблемы в решении задачи. Но мы не знаем его ежедневной нормы по плану
3.Надеваем красную шляпу – ребята выскажите свои эмоции предположения по данному вопросу, есть ли у вас предложения, как решить задачу, что необходимо сделать.
4.Надеваем желтую шляпу – мы видим, что у …. Давайте посчитаем, …. Каким правилом можно воспользоваться, чтобы узнать ….?
5. Надеваем зеленую шляпу – мы определили, что ……
6.Надеваем синюю шляпу – решим полученное уравнение
Решение
Пусть тракторист по плану в день должен вспахать х га.,- дневная норма
но по факту он вспахивал по (х+2) га . Тогда
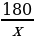 - дней по плану для выполнение задания;
- дней по плану для выполнение задания;
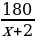 - дней по факту для выполнение задания.
- дней по факту для выполнение задания.
По условию задачи составляем и решаем уравнение:
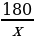 -
- 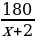 = 1
= 1
ОДЗ: х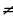 0, х
0, х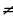 -2
-2
Общий знаменатель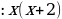 .
.
Умножим обе части уравнения на 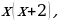
получим 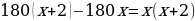 ,
,
180х +360 – 180х =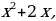
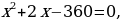 D = 4+ 1440 =1444
D = 4+ 1440 =1444 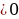 , 2 корня
, 2 корня
х= (-2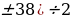 ,
, 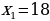 - удовлетворяет условию задачи
- удовлетворяет условию задачи
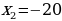 – не удовлетворяет условию задачи так, как количество гектаров не может быть отрицателным числом.
– не удовлетворяет условию задачи так, как количество гектаров не может быть отрицателным числом.
180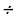 18 =10 ( дней) по плану, а по факту – (10-1) = 9 ( дней).
18 =10 ( дней) по плану, а по факту – (10-1) = 9 ( дней).
Ответ: 9 дней.
VII. Информация о домашнем задании, инструктаж по его выполнению
3.10. Решите уравнение 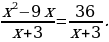
3.11. Решите уравнение 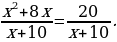
3.12. Решите уравнение 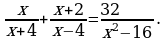
3.13. Решите уравнение 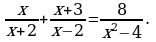
VIII.Рефлексия
Применение метода на этапе РЕФЛЕКСИИ:
Белая: На мой взгляд, больше всего удалось….. (факты, информация).
Красная: Меня удивило….. (эмоции, интуиция).
Чёрная: Я думаю, что ……. (критика, оценка).
Жёлтая: Для меня было открытием то, что………….. (логический позитив, оптимизм).
Зелёная: На будущее я учту…………. (креатив, новая идея).
Синяя: Я могу похвалить за….. (обобщение).
 С помощью светофора ученики оценивают свою работу.
С помощью светофора ученики оценивают свою работу.
 Урок прошел удачно: я участвовал в работе класса, с заданиями справился успешно. Я очень доволен собой.
Урок прошел удачно: я участвовал в работе класса, с заданиями справился успешно. Я очень доволен собой.
 Сегодня на уроке не все задания оказались легкими. Мне было трудно, но я справился. Я доволен собой!
Сегодня на уроке не все задания оказались легкими. Мне было трудно, но я справился. Я доволен собой!
Задания на уроке оказались трудными. Мне нужна помощь!
Список использованной литературы: (слайд 13)
1. Макарычев Ю.Н. Алгебра.8 класс.- М.:«Просвещение»,2016
2. Жохов В.И., Карташева Г.Д. Уроки алгебры в 8 классе.-М.:«Просвещение»,2014
3. Ященко И.В. ОГЭ (ГИА-9): 3000 задач с ответами по математике. Все задания части 1.-М.: Издательство «Экзамен», 2015
4. Лаппо Л.Д. ЕГЭ. Математика. Тематические тренировочные задания. -М.: Издательство «Экзамен», 2015







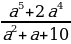 ; Ответ :0 б)
; Ответ :0 б) 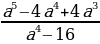 . Ответ: 0 (Работа в диалоге)
. Ответ: 0 (Работа в диалоге)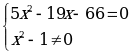
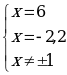
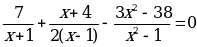
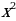
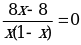
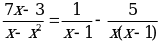
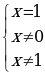 нет решений
нет решений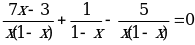

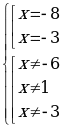 ример 3.
ример 3.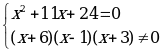
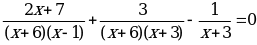
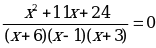 x = -8 ОДЗ: х
x = -8 ОДЗ: х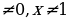
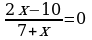 ; б)
; б) 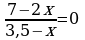 ; в)
; в) 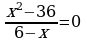 .
.
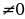 имеет один корень,
имеет один корень, 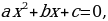 где x - переменная, а , в и с – некоторые числа, причём а
где x - переменная, а , в и с – некоторые числа, причём а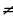 0.
0.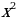 равен 1, называется приведенным квадратным уравнением.
равен 1, называется приведенным квадратным уравнением.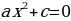 , где с
, где с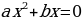 , где в
, где в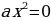 .
.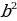 - 4ac называют дискриминантом квадратного уравнения и его обозначают буквой D =
- 4ac называют дискриминантом квадратного уравнения и его обозначают буквой D =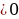 , уравнение имеет два корня,
, уравнение имеет два корня,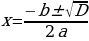 , где D =
, где D =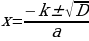 , где D =
, где D =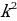 - ac для квадратного уравнения
- ac для квадратного уравнения 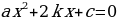 ,
,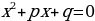 равна второму коэффициенту, взятому с противоположным знаком, т.е. х1 + х2 = -
равна второму коэффициенту, взятому с противоположным знаком, т.е. х1 + х2 = -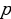 ,
, 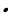 х2 =
х2 = 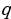 ..
..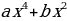 + c = 0, где
+ c = 0, где 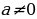 являющемся квадратным относительно
являющемся квадратным относительно 



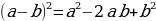
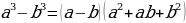
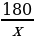 - дней по плану для выполнение задания;
- дней по плану для выполнение задания;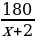 - дней по факту для выполнение задания.
- дней по факту для выполнение задания.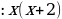 .
.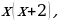
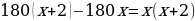 ,
, 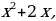
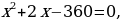 D = 4+ 1440 =1444
D = 4+ 1440 =1444 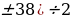 ,
, 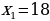 - удовлетворяет условию задачи
- удовлетворяет условию задачи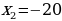 – не удовлетворяет условию задачи так, как количество гектаров не может быть отрицателным числом.
– не удовлетворяет условию задачи так, как количество гектаров не может быть отрицателным числом.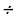 18 =10 ( дней) по плану, а по факту – (10-1) = 9 ( дней).
18 =10 ( дней) по плану, а по факту – (10-1) = 9 ( дней).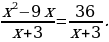
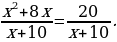
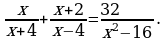
 С помощью светофора ученики оценивают свою работу.
С помощью светофора ученики оценивают свою работу. Урок прошел удачно: я участвовал в работе класса, с заданиями справился успешно. Я очень доволен собой.
Урок прошел удачно: я участвовал в работе класса, с заданиями справился успешно. Я очень доволен собой. Сегодня на уроке не все задания оказались легкими. Мне было трудно, но я справился. Я доволен собой!
Сегодня на уроке не все задания оказались легкими. Мне было трудно, но я справился. Я доволен собой!



















