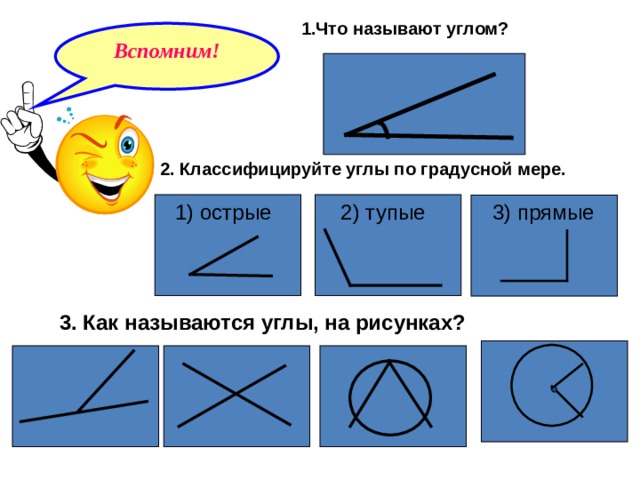
1.Что называют углом?
Вспомним!
2. Классифицируйте углы по градусной мере.
3) прямые
2) тупые
1) острые
3. Как называются углы, на рисунках?
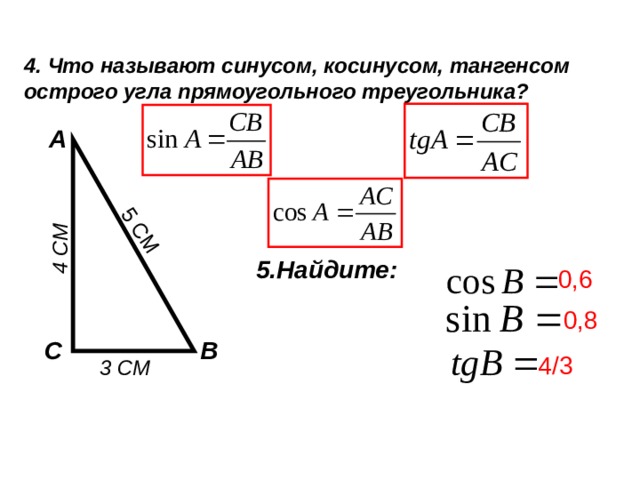
4 СМ
5 СМ
4. Что называют синусом, косинусом, тангенсом острого угла прямоугольного треугольника?
А
5.Найдите:
0,6
0,8
С
В
4/3
3 СМ

Двугранный угол. Угол между плоскостями

ЦЕЛИ УРОКА:
- ВВЕСТИ ПОНЯТИЕ ДВУГРАННОГО УГЛА И ЕГО ЛИНЕЙНОГО УГЛА;
- СФОРМИРОВАТЬ КОНСТРУКТИВНЫЙ НАВЫК НАХОЖДЕНИЯ УГЛА МЕЖДУ ПЛОСКОСТЯМИ.
- РАССМОТРЕТЬ ЗАДАЧИ НА ПРИМЕНЕНИЕ ЭТИХ ПОНЯТИЙ;
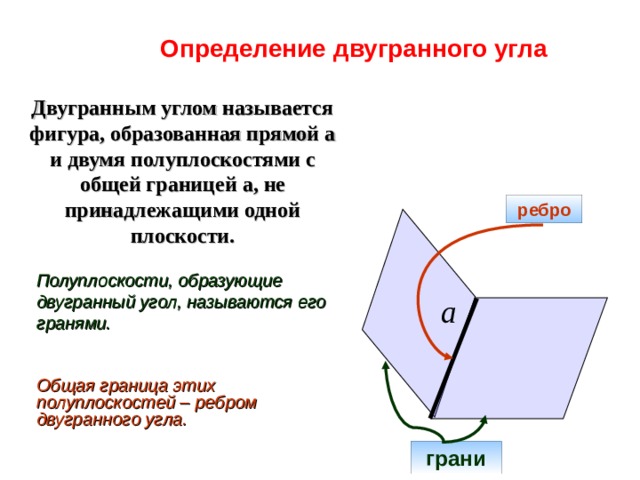
Определение двугранного угла
Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a , не принадлежащими одной плоскости.
ребро
Полуплоскости, образующие двугранный угол, называются его гранями.
Общая граница этих полуплоскостей – ребром двугранного угла.
грани

В обыденной жизни, форму двугранного угла имеют
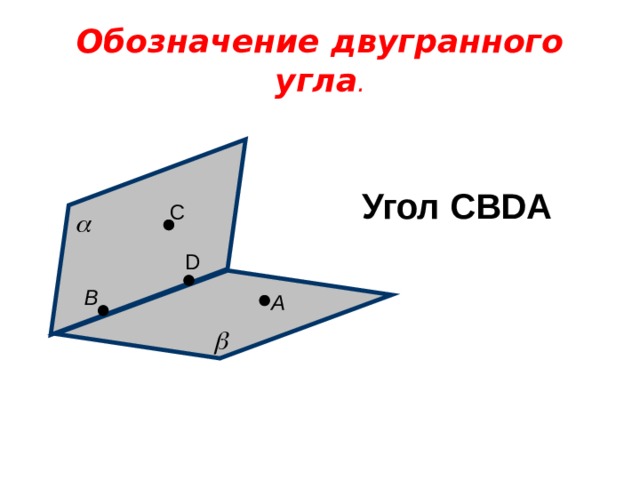
Обозначение двугранного угла .
Угол CBDA
С
D
В
А

Измерение двугранных углов. Линейный угол.
Величиной двугранного угла называется величина его линейного угла.
Р
М
В
Р
АВМС =
А
С
D
Угол Р – линейный угол двугранного угла АВМС
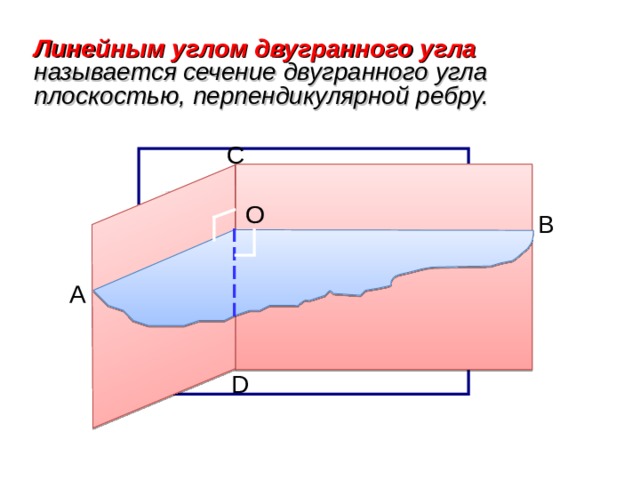
Линейным углом двугранного угла называется сечение двугранного угла плоскостью, перпендикулярной ребру.
С
О
В
А
D
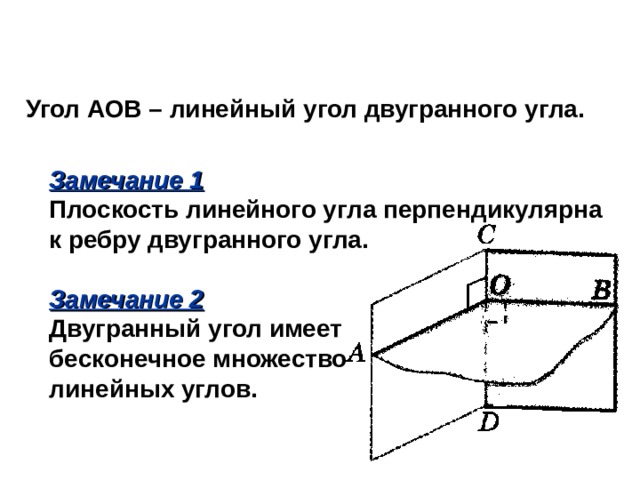
Угол АОВ – линейный угол двугранного угла.
Замечание 1
Плоскость линейного угла перпендикулярна
к ребру двугранного угла.
Замечание 2
Двугранный угол имеет
бесконечное множество
линейных углов.
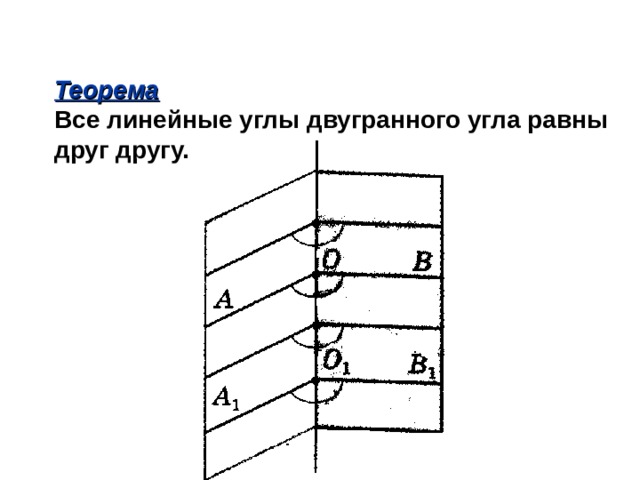
Теорема
Все линейные углы двугранного угла равны
друг другу.
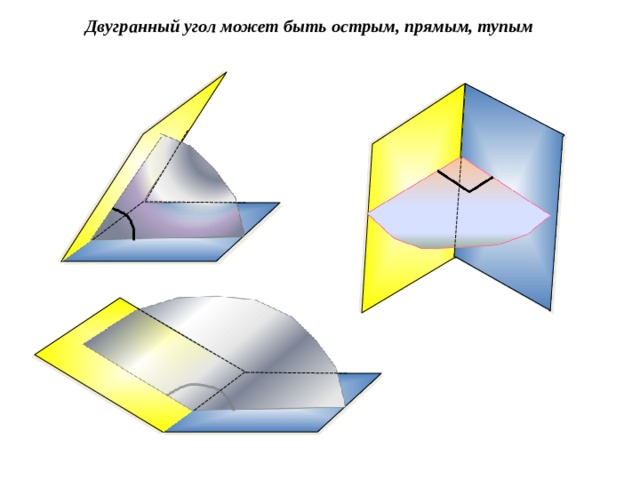
Двугранный угол может быть острым, прямым, тупым
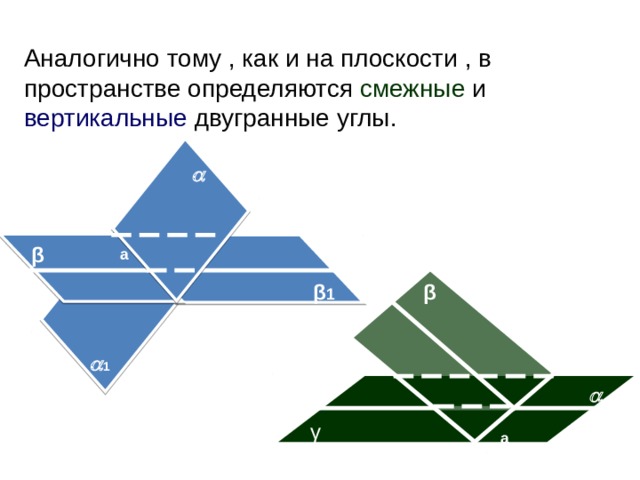
Аналогично тому , как и на плоскости , в пространстве определяются смежные и вертикальные двугранные углы.
β
а
β 1
β
1
γ
а

Способ нахождения (построения) линейного угла.
1 . Найти ( увидеть) ребро и грани двугранного угла
2. В гранях найти направления ( прямые) перпендикулярные ребру
3. (при необходимости) заменить выбранные направления параллельными им лучами с общим началом на ребре двугранного угла
При изображении сохраняется параллельность и отношение длин параллельных отрезков
Н-я
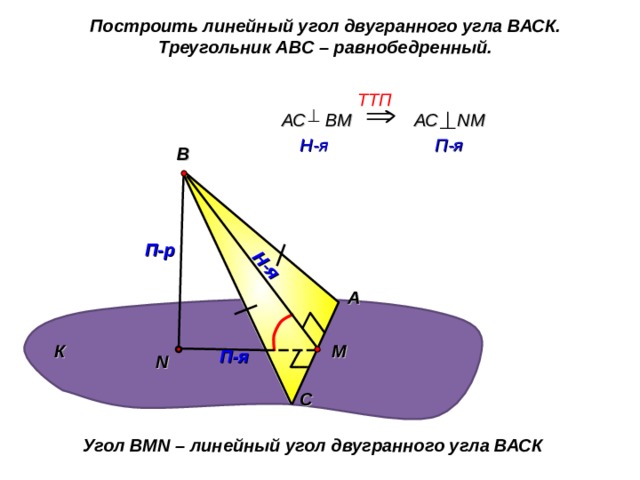
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
TT П
АС ВМ
АС N М
П-я
H -я
В
П-р
А
К
M
П-я
N
С
Угол В MN – линейный угол двугранного угла ВАСК
15
Н-я
П-я
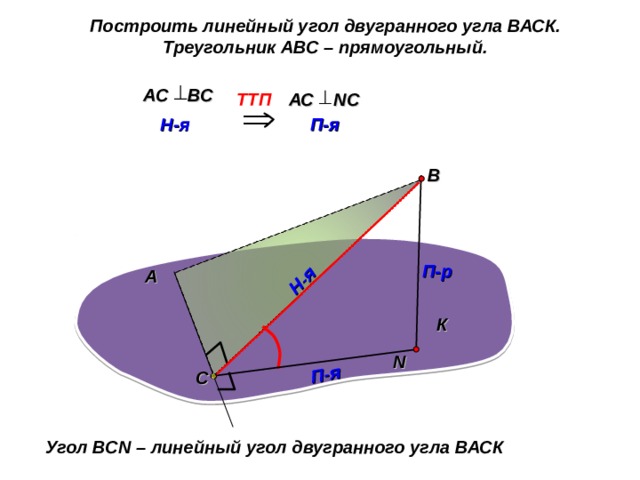
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
АС ВС
TT П
АС N С
П-я
H -я
В
П-р
А
К
N
С
Угол ВС N – линейный угол двугранного угла ВАСК
16
Н-я
П-я
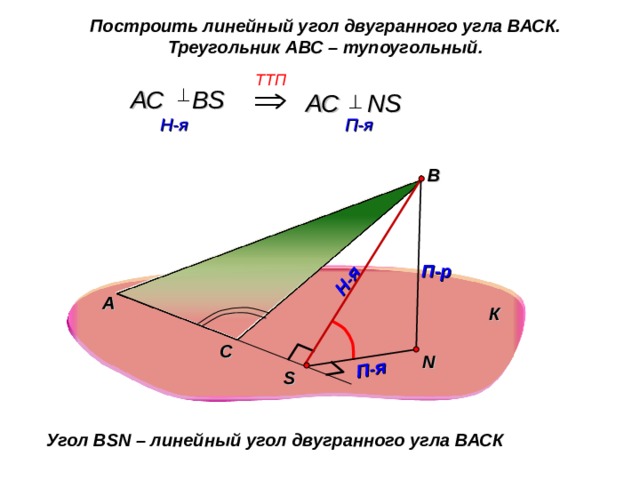
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – тупоугольный.
TT П
АС В S
АС NS
H -я
П-я
В
П-р
А
К
С
N
S
Угол В SN – линейный угол двугранного угла ВАСК
17
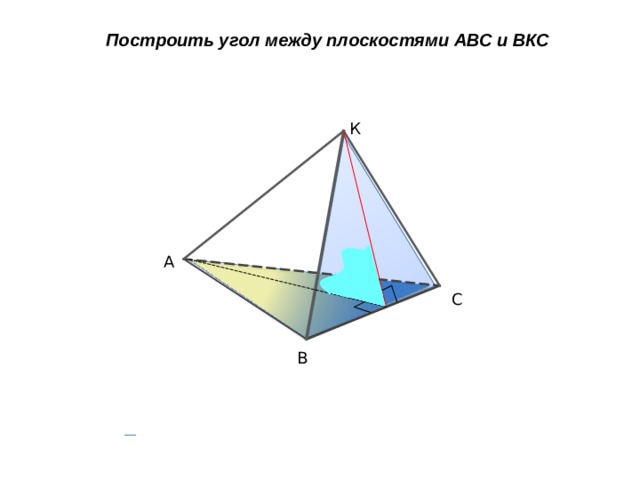
Построить угол между плоскостями АВС и ВКС
К
А
С
В
18

Построить угол между плоскостями АВСД и АСД 1
Д 1
С 1
А 1
В 1
Д
С
А
В
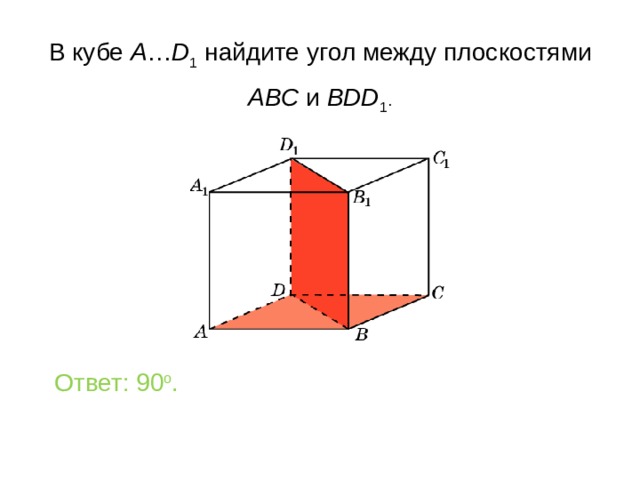
В кубе A … D 1 найдите уг ол между плоскостями
ABC и BDD 1 .
Ответ: 90 o .
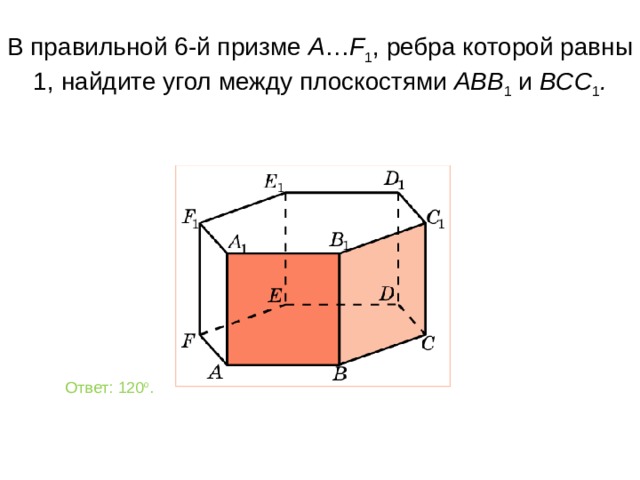
В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите у гол между плоскостями ABB 1 и BCC 1 .
Ответ: 120 о .

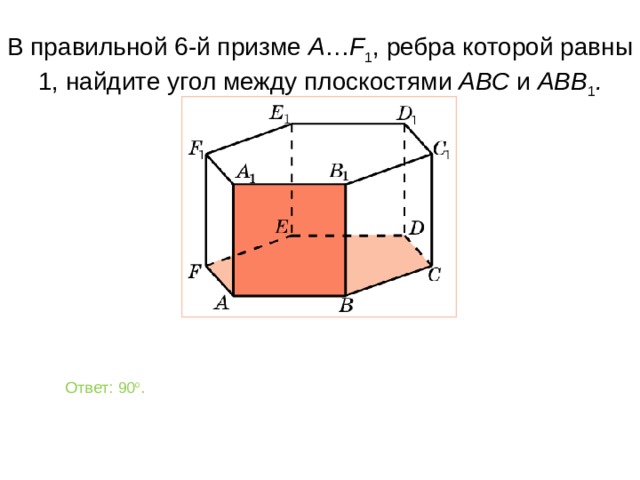
В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите у гол между плоскостями ABC и ABB 1 .
Ответ: 90 о .
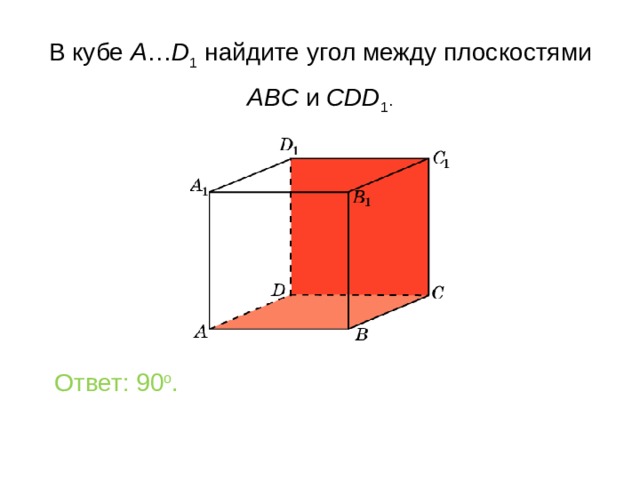
В кубе A … D 1 найдите уг ол между плоскостями
ABC и CDD 1 .
Ответ: 90 o .
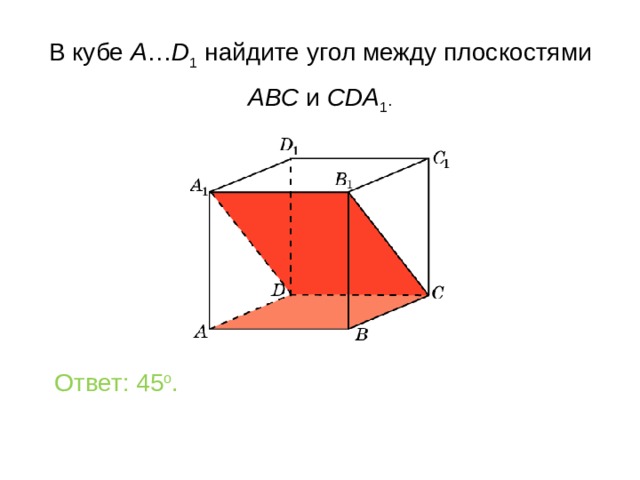
В кубе A … D 1 найдите уг ол между плоскостями
ABC и CDA 1 .
Ответ: 45 o .
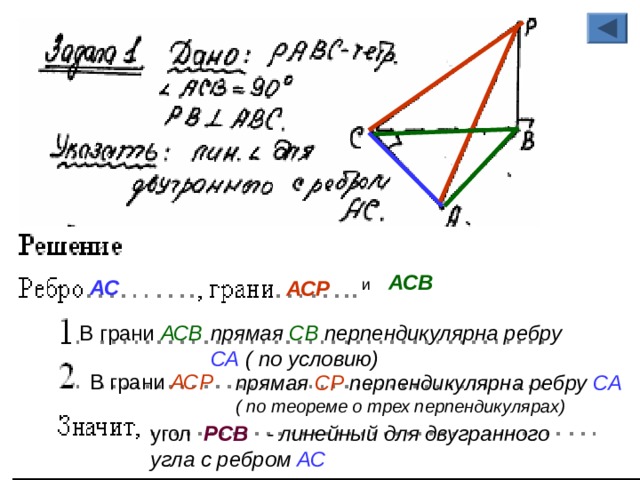
и АСВ
АС
АСР
В грани АСВ
прямая СВ перпендикулярна ребру СА ( по условию)
В грани АСР
прямая СР перпендикулярна ребру СА
( по теореме о трех перпендикулярах)
угол РСВ - линейный для двугранного угла с ребром АС
К
АС
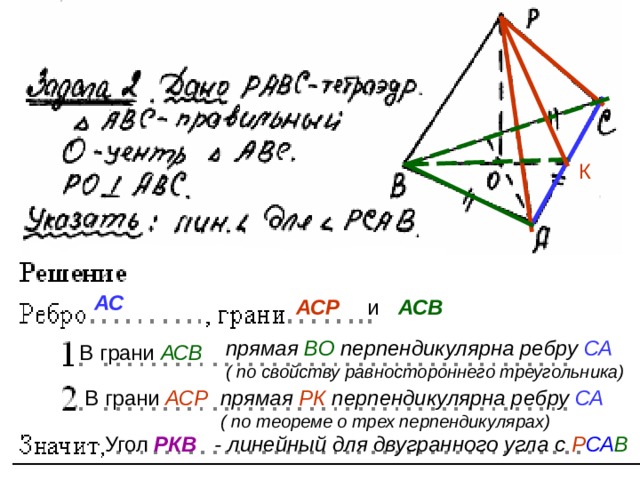
и АСВ
АСР
прямая ВО перпендикулярна ребру СА
( по свойству равностороннего треугольника)
В грани АСВ
прямая РК перпендикулярна ребру СА
( по теореме о трех перпендикулярах)
В грани АСР
Угол РКВ - линейный для двугранного угла с Р СА В

СПАСИБО ЗА УРОК